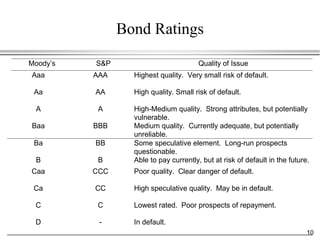
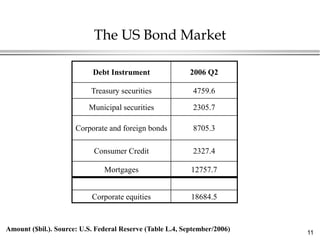
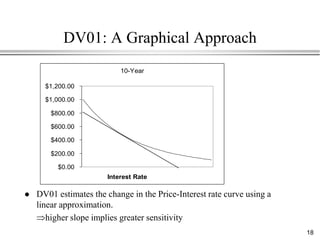
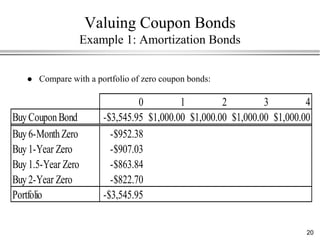
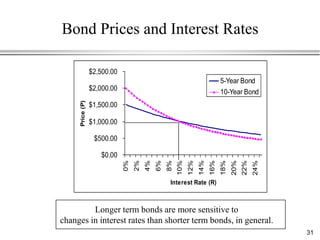
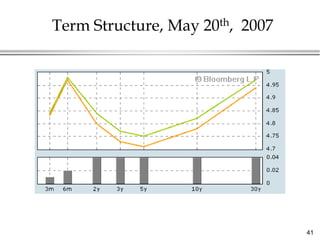
This document provides an overview of bond valuation and interest rate sensitivity. It begins with an introduction to bonds and bond markets, including different types of bonds such as zero-coupon bonds and coupon bonds. It then discusses how to value zero-coupon bonds and coupon bonds using present value calculations. The document also examines how bond prices are inversely related to interest rates and how duration can be used to measure a bond's interest rate sensitivity.

1. Bond Valuation An Overview
 Introduction to bonds and bond markets
» What are they? Some examples
 Zero coupon bonds
» Valuation
» Interest rate sensitivity
 Coupon bonds
» Valuation
» Interest rate sensitivity
 The term structure of interest rates
1

2. What is a Bond?
 A bond is a security that obligates the issuer to make specified interest
and principal payments to the holder on specified dates.
» Coupon rate
» Face value (or par)
» Maturity (or term)
 Bonds are also called fixed income securities.
 Bonds differ in several respects:
» Repayment type
» Issuer
» Maturity
» Security
» Priority in case of default
2

3. Repayment Schemes
 Pure Discount or Zero-Coupon Bonds
» Pay no coupons prior to maturity.
» Pay the bond‟s face value at maturity.
 Coupon Bonds
» Pay a stated coupon at periodic intervals prior to maturity.
» Pay the bond‟s face value at maturity.
 Floating-Rate Bonds
» Pay a variable coupon, reset periodically to a reference rate.
» Pay the bond‟s face value at maturity.
 Perpetual Bonds (Consols)
» No maturity date.
» Pay a stated coupon at periodic intervals.
 Annuity or Self-Amortizing Bonds
» Pay a regular fixed amount each payment period.
» Principal repaid over time rather than at maturity.
3

4. Types of Bonds: Issuers
Bonds Issuer
Government Bonds US Treasury, Government Agencies
Mortgage-Backed Securities Government agencies (GNMA etc)
Municipal Bonds State and local government
Corporate Bonds Corporations
Asset-Back Securities Corporations
4

5. U.S. Government Bonds
 Treasury Bills
» No coupons (zero coupon security)
» Face value paid at maturity
» Maturities up to one year
 Treasury Notes
» Coupons paid semiannually
» Face value paid at maturity
» Maturities from 2-10 years
5

6. U.S. Government Bonds (Cont.)
 Treasury Bonds
» Coupons paid semiannually
» Face value paid at maturity
» Maturities over 10 years
» The 30-year bond is called the long bond.
 Treasury Strips
» Zero-coupon bond
» Created by “stripping” the coupons and principal from Treasury
bonds and notes.
 No default risk. Considered to be risk free.
 Exempt from state and local taxes.
 Sold regularly through a network of primary dealers.
 Traded regularly in the over-the-counter market.
6

7. Agency and Municipal Bonds
 Agency bonds: mortgage-backed bonds
» Bonds issued by U.S. Government agencies that are backed by a
pool of home mortgages.
» Self-amortizing bonds. (mostly monthly payments)
» Maturities up to 30 years.
» Prepayment risk.
 Municipal bonds
» Maturities from one month to 40 years.
» Usually exempt from federal, state, and local taxes.
» Generally two types:
– Revenue bonds
– General Obligation bonds
» Riskier than U.S. Government bonds.
7

8. Corporate Bonds
 Bonds issued by corporations
» Bonds vs. Debentures
» Fixed-rate versus floating-rate bonds.
» Investment-grade vs. Below investment-grade bonds.
» Additional features:
– call provisions
– convertible bonds
– puttable bonds
8

9. Seniority of Corporate Bonds
 In case of default, different classes of bonds have different
claim priority on the assets of a corporation.
 Secured Bonds (Asset-Backed)
» Secured by real property.
» Ownership of the property reverts to the bondholders upon default.
 Debentures
» Same priority as general creditors.
» Have priority over stockholders, but subordinate to secured debt.
9

10. Bond Ratings
Moody’s S&P Quality of Issue
Aaa AAA Highest quality. Very small risk of default.
Aa AA High quality. Small risk of default.
A A High-Medium quality. Strong attributes, but potentially
vulnerable.
Baa BBB Medium quality. Currently adequate, but potentially
unreliable.
Ba BB Some speculative element. Long-run prospects
questionable.
B B Able to pay currently, but at risk of default in the future.
Caa CCC Poor quality. Clear danger of default.
Ca CC High speculative quality. May be in default.
C C Lowest rated. Poor prospects of repayment.
D - In default.
10

11. The US Bond Market
Debt Instrument 2006 Q2
Treasury securities 4759.6
Municipal securities 2305.7
Corporate and foreign bonds 8705.3
Consumer Credit 2327.4
Mortgages 12757.7
Corporate equities 18684.5
Amount ($bil.). Source: U.S. Federal Reserve (Table L.4, September/2006) 11

12. Bond Valuation: Zero Coupon Bonds
B = Market price of the Bond of bond
F = Face value
R = Annual percentage rate
m = compounding period (annual  m = 1, semiannual  m = 2,…)
i = Effective periodic interest rate; i=R/m
T = Maturity (in years)
N = Number of compounding periods; N = T*m
 Two cash flows to purchaser of bond:
» -B at time 0
» F at time T
 What is the price of a bond?
Use present value formula:
F
B N
1 i
12

13. Valuing Zero Coupon Bonds:
An Example
 Value a 5 year, U.S. Treasury strip with face value of $1,000. The APR is
R=7.5% with annual compounding? What about quarterly compounding?
 What is the APR on a U.S. Treasury strip that pays $1,000 in exactly 7 years
and is currently selling for $591.11 under annual compounding? Semi-annual
compounding?
13

14. Interest Rate Sensitivity:
Zero Coupon Bonds
 Consider the following 1, 2 and 10-year zero-coupon
bonds, all with
» face value of F=$1,000
» APR of R=10%, compounded annually.
We obtain the following table for increases and decreases of the
interest rate by 1%:
Interest Rate Bond 1 Bond 2 Bond 3
1-Year 2-Year 10-Year
9.0% $917.43 $841.68 $422.41
10.0% $909.09 $826.45 $385.54
11.0% $900.90 $811.62 $352.18
 Bond prices move up if interest rates drop, decrease if
interest rates rise
14

15. Bond Prices and Interest Rates
$1,200
 Bond prices are
$1,000 inversely related
to IR
$800  Longer term
$600
bonds are more
sensitive to IR
$400 1-Year changes than
2-Year short term
$200 bonds
10-Year
$0  The lower the
0.0% 5.0% 10.0% 15.0% 20.0% 25.0% IR, the more
sensitive the
price.
15

16. Measuring Interest Rate Sensitivity
Zero Coupon Bonds
 We would like to measure the interest rate sensitivity of a bond or a
portfolio of bonds.
» How much do bond prices change if interest rates change by a small
amount?
» Why is this important?
 Use “Dollar value of a one basis point decrease” (DV01):
» Basis point (bp): 1/100 of one percentage point =0.01%=0.0001
» Calculate DV01:
– Method 1: Difference of moving one basis point down:
DV01= B(R-0.01%)-B(R).
– Method 2: Difference of moving 1/2bp down minus 1/2pb up:
DV01=B(R-0.005%) -B(R+0.005%).
– Method 3: Use calculus:
B
DV 01 0.0001
R
16

17. Computing DV01: An Example
 Reconsider the 1, 2 and 10- year bonds discussed before:
Interest Rate Bond 1 Bond 2 Bond 3
1-Year 2-Year 10-Year
9.990% $909.1736 $826.5966 $385.8940
9.995% $909.1322 $826.5214 $385.7186
10.000% $909.0909 $826.4463 $385.5433
10.005% $909.0496 $826.3712 $385.3681
Method 1 $0.082652 $0.150283 $0.350669
Method 2 $0.082645 $0.150263 $0.350494
Method 3 $0.082645 $0.150263 $0.350494
 Method 3:
B $1,000 1
0.0001 T 0.0001 T * $0.10 *
R 1.10T 1 1.10T 1
17

18. DV01: A Graphical Approach
10-Year
$1,200.00
$1,000.00
$800.00
$600.00
$400.00
$200.00
$0.00
Interest Rate
 DV01 estimates the change in the Price-Interest rate curve using a
linear approximation.
higher slope implies greater sensitivity
18

19. Valuing Coupon Bonds
Example 1: Amortization Bonds
 Consider Amortization Bond
» T=2
» m=2
» C=$2,000 c = C/m = $2,000/2 = $1,000
» R=10%  i = R/m = 10%/2 = 5%
 How can we value this security?
» Brute force discounting
» Similar to another security we already know how to value?
» Replication
19

20. Valuing Coupon Bonds
Example 1: Amortization Bonds
 Compare with a portfolio of zero coupon bonds:
0 1 2 3 4
Buy Coupon Bond -$3,545.95 $1,000.00 $1,000.00 $1,000.00 $1,000.00
Buy 6-Month Zero -$952.38
Buy 1-Year Zero -$907.03
Buy 1.5-Year Zero -$863.84
Buy 2-Year Zero -$822.70
Portfolio -$3,545.95
20

21. A First Look at Arbitrage
 Reconsider amortization bond; suppose bond
trades at $3,500 (as opposed to computed price of
$3,545.95)
» Can we make a profit without any risk?
– What is the strategy?
– What is the profit?
21

22. A First Look at Arbitrage
 Reconsider amortization bond; suppose bond trades at $3,500 (as
opposed to computed price of $3,545.95)
» Can make risk less profit
– Buy low: buy amortization bond
– Sell high: Sell portfolio of zero coupon bonds
Time Period
0 1 2 3 4
Buy Coupon Bond -$3,500.00 $1,000.00 $1,000.00 $1,000.00 $1,000.00
Sell 6-Month Zero $952.38 -$1,000.00 $0.00 $0.00 $0.00
Sell 1-Year Zero $907.03 $0.00 -$1,000.00 $0.00 $0.00
Sell 1.5-Year Zero $863.84 $0.00 $0.00 -$1,000.00 $0.00
Sell 2-Year Zero $822.70 $0.00 $0.00 $0.00 -$1,000.00
Portfolio $3,545.95 -$1,000.00 -$1,000.00 -$1,000.00 -$1,000.00
Net Cash Flow $45.95 $0.00 $0.00 $0.00 $0.00
– riskless profit of $45.95
– no riskless profit if price is correct 22

23. Valuation of Coupon Bonds:
Example 2: Straight Bonds
 What is the market price of a U.S. Treasury bond that has a coupon
rate of 9%, a face value of $1,000 and matures exactly 10 years from
today if the interest rate is 10% compounded semiannually?
0 6 12 18 24 ... 120 Months
45 45 45 45 1045
23

24. Valuing Coupon Bonds
The General Formula
 What is the market price of a bond that has an annual coupon C, face
value F and matures exactly T years from today if the required rate of
return is R, with m-periodic compounding?
» Coupon payment is: c = C/m
» Effective periodic interest rate is: i = R/m
» number of periods N = Tm
0 1 2 3 4 ... … N
c c c c… … c+F
B Annuity Zero
c 1 F
1 N N
i 1 i 1 i
24

25. The Concept of a “Yield to Maturity”
 So far we have valued bonds by using a given interest rate,
then discounted all payments to the bond.
 Prices are usually given from trade prices
» need to infer interest rate that has been used
Definition: The yield to maturity is that interest rate that
equates the present discounted value of all future payments
to bondholders to the market price:
 Algebraic:
c 1 F
B 1 N N
yield / m 1 yield / m 1 yield / m
25

26. Yield to Maturity
A Graphical Interpretation
$2,500.00
$2,000.00
$1,500.00
$1,000.00
$500.00
$0.00
0%
2%
4%
6%
8%
10%
12%
14%
16%
18%
20%
22%
24%
 Consider a U.S. Treasury bond that has a coupon rate of 10%, a face value of
$1,000 and matures exactly 10 years from now.
» Market price of $1,500, implies a yield of 3.91% (semi-annual
compounding); for B=$1,000 we obviously find R=10%.
26

27. Interest Rate Sensitivity:
Coupon Bonds
 Coupon bonds can be represented as portfolios of zero-
coupon bonds
» Implication for price sensitivity
 Consider purchasing the US Treasury bond discussed
earlier (10 year, 9% coupon, $1,000 face)
» Suppose immediately thereafter interest rates fall to 8%,
compounded semiannually.
» Suppose immediately thereafter interest rate rises to 12%
compounded semiannually.
» Suppose the interest rate equals 9%, compounded semiannually.
 What are the pricing implications of these scenarios?
27

28. Implication of Interest Rate Changes on
Coupon Bond Prices
 Recall the general formula:
c 1 F
B 1 N N
i 1 i 1 i
 What is the price of the bond if the APR is 8% compounded
semiannually?
 Similarly:
If R=12%: B=$ 827.95
If R= 9%: B=$1,000.00
28

29. Relationship Between Coupon Bond
Prices and Interest Rates
 Bond prices are inversely related to interest rates (or
yields).
 A bond sells at par only if its interest rate equals the
coupon rate
 A bond sells at a premium if its coupon rate is above the
interest rate.
 A bond sells at a discount if its coupon rate is below the
interest rate. 29

30. DV01 and Coupon Bonds
 Consider two bonds with 10% annual coupons with maturities of 5
years and 10 years.
 The APR is 8%
 What are the responses to a .01% (1bp) interest rate change?
Yield 5-Year Bond $ Change % Change 10-Year Bond $ Change % Change
7.995% $1,080.06 $0.21019 0.0195% $1,134.57 $0.36585 0.0323%
8.000% $1,079.85 $1,134.20
8.005% $1,079.64 -$0.21013 -0.0195% $1,133.84 -$0.36569 -0.0322%
DV01 $0.42032 $0.73154
 Does the sensitivity of a coupon bond always increase with the term to
maturity?
30

31. Bond Prices and Interest Rates
$2,500.00
5-Year Bond
$2,000.00 10-Year Bond
Price (P)
$1,500.00
$1,000.00
$500.00
$0.00
0%
2%
4%
6%
8%
10%
12%
14%
16%
18%
20%
22%
24%
Interest Rate (R)
Longer term bonds are more sensitive to
changes in interest rates than shorter term bonds, in general.
31

32. Bond Yields and Prices
 Consider the following two bonds:
» Both have a maturity of 5 years
» Both have yield of 8%
» First has 6% coupon, other has 10% coupon, compounded
annually.
 Then, what are the price sensitivities of these bonds, measured by
DV01 as for zero coupon bonds?
Yield 6%-Bond $ Change % change 10%-Bond $ Change % change
7.995% $920.33 $0.1891 $1,080.06 $0.2102
8.000% $920.15 $1,079.85
8.005% $919.96 ($0.1891) $1,079.64 ($0.2101)
0.0411% 0.0389%
DV01 $0.3782 $0.4203
 Why do we get different answers for two bonds with the same yield
and same maturity?
32

33. Maturity and Price Risk
 Zero coupon bonds have well-defined relationship
between maturity and interest rate sensitivity:
 Coupon bonds can have different sensitivities for
the same maturity
» DV01 now depends on maturity and coupon
 Need concept of “average maturity” of coupon
bond:
» Duration
33

34. Duration
 Duration is a weighted average term to maturity where the
weights are relative size of the contemporaneous cash flow.
PV (c ) PV (c ) PV (c )
Duration T 1 T 2  T N T PV (F)
1 B 2 B N B N B
 Duration is a unitless number that quantifies the percentage
change in a bond‟s price for a 1 percentage change in the
interest rate. B
B 1 R B
Duration
R B R
1 R
34

35. Duration (cont.)
 The duration of a bond is less than its time to maturity (except for
zero coupon bonds).
 The duration of the bond decreases the greater the coupon rate.
This is because more weight (present value weight) is being given
to the coupon payments.
 As market interest rate increases, the duration of the bond
decreases. This is a direct result of discounting. Discounting at a
higher rate means lower weight on payments in the far future.
Hence, the weighting of the cash flows will be more heavily
placed on the early cash flows -- decreasing the duration.
 Modified Duration = Duration / (1+yield)
35

36. A Few Bond Markets Statistics
U.S. Treasuries, May 20th 2007.
Bills
MATURITY DISCOUNT/YIELD DISCOUNT/YIELD TIME
DATE CHANGE
3-Month 08/16/2007 4.72 / 4.84 0.01 / .010 13:41
6-Month 11/15/2007 4.78 / 4.98 0.01 / .015 13:41
Notes/Bonds
COUPON MATURITY CURRENT PRICE/YIELD TIME
DATE PRICE/YIELD CHANGE
2-Year 4.500 04/30/2009 99-121⁄4 / 4.84 -0-02 / .03514:08
3-Year 4.500 05/15/2010 99-081⁄2 / 4.77 -0-031⁄2 / .040 14:06
5-Year 4.500 04/30/2012 98-281⁄2 / 4.75 -0-06 / .04314:07
10-Year 4.500 05/15/2017 97-15 / 4.82 -0-091⁄2 / .038 14:07
30-Year 4.750 02/15/2037 96-17+ / 4.97 -0-17 / .03514:07
36

37. Spot Rates
 A spot rate is a rate agreed upon today, for a loan that is to be
made today
» r1=5% indicates that the current rate for a one-year loan is 5%.
» r2=6% indicates that the current rate for a two-year loan is 6%.
» Etc.
 The term structure of interest rates is the series of spot rates
r1, r2, r3,…
» We can build using STRIPS or coupon bond yields.
» Explanations of the term structure.
37

38. The Term Structure of Interest Rates
An Example
Yield
6.00
5.75
5.00
1 2 3 Maturity
38

39. Term Structure, July 1st 2005.
39

40. Term Structure, September 12th, 2006
40

41. Term Structure, May 20th, 2007
41

42. Term Structure of Interest Rates
42

43. 43

44. Summary
 Bonds can be valued by discounting their future cash
flows
 Bond prices change inversely with yield
 Price response of bond to interest rates depends on term
to maturity.
» Works well for zero-coupon bond, but not for coupon bonds
 Measure interest rate sensitivity using „DV01‟ and
duration.
 The term structure implies terms for future borrowing:
» Forward rates
» Compare with expected future spot rates
44