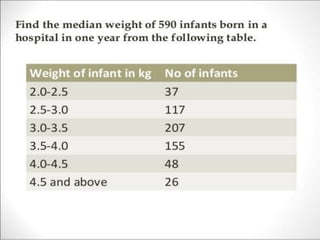
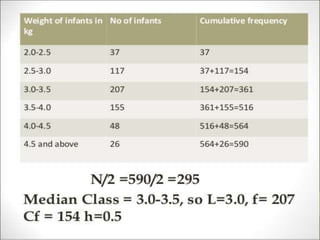
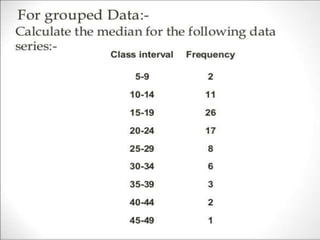
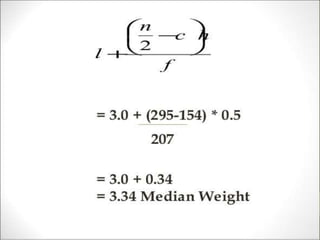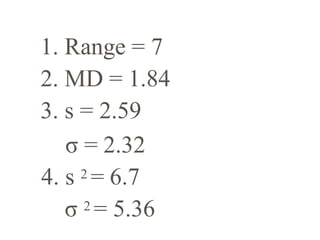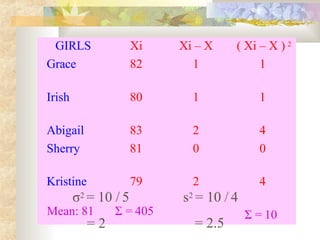
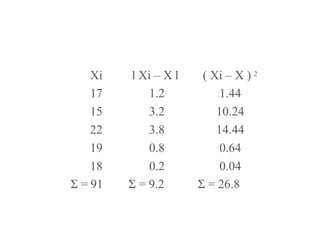
Here are the measures of central tendency and variability I calculated from the given data: Measures of Central Tendency: Mean = Sum of all values / Total number of observations = (60 + 70 + 80 + 90 + 100 + 60 + 70 + 80 + 81 + 79) / 10 = 771 / 10 = 77.1 Measures of Variability: Range = Highest value - Lowest value = 100 - 60 = 40 Mean Deviation = Sum of absolute deviations from the mean / Total number of observations = |60 - 77.1| + |70 - 77.1| + ... + |79 - 77.1| / 10 = 62.1

1. BIOSTATISTICS: General
introduction & Central Tendency
Mohmmad Amil Rahman
S.R.
Dr. R.P.G.M.College Kangra at Tanda(H.P.)

2. BIOSTATISTICS
• It is the branch of statistics concernedwith mathematical
facts and data related to biological events.
• It is the science that helps in managing medical
uncertainties.
• Biostatistics covers applications and contributions not
only from health, medicines and, nutrition but also
from fields such as genetics, biology, epidemiology, and
many others.

3. BRANCHES OF BIOSTATISTICS
• Descriptive Biostatistics
 Methods of producing quantitative summaries of information in
biological sciences.
 Tabulation and Graphical presentation
• Inferential Biostatistics
• Methods of making generalizations about a larger group based
on information about a sample of that group in biological sciences.
• Primarily performed in two ways:
• O Estimation
• O Testing of hypothesis

4. HISTORY
• Sir Francis Galton is considered as the
Father of Biostatistics.
• In 1929,a huge paper on application of
statistics was published in physiology journal
by Dunn.
• In 1937, 15 articles on statistical methods by
Austin Bradford Hill, were published in
book form.

5. Sources of medical Uncertainties
• Intrinsic due to biological, environmental and
sampling factors.
• Natural variation among methods, observers
and instruments etc.
• Errors in measurement or assessment or errors
in knowledge.

6. • Biological, due to age, gender, heredity, party, height, weight
etc. Also due to variation in anatomical, physiological and
biomechanical parameters.
• In nature, blood pressure, pulse rate, action of a drug or any
other measurement or counting varies not only from person to
person but also from group to group.
• Variation more than natural limits may be pathological, i.e.,
abnormal due to the play of certain external factors. Hence
biostatistics may also be called a science of variation.

7. • It is the science(biostatistics) which deals with
development andapplication of the most
appropriate methods for the:
Collection of data.
Presentation of the collected data.
Analysis and interpretation of the results.
Making decisions on the basis of such analysis.

8. ROLE OF BIOSTATISTICIANS
 Identify and develop treatments for disease
and estimate their effects.
 Identify risk factors for diseases.
 Design, monitor, analyze, interpret, and report
results of clinical studies.
 Develop statistical methodologies to address
questions arising from medical/public health
data.
 Locate , define & measure extent of disease
 Main objective  improve the health of
individual &community

9. APPLICATION OF BIOSTATISTICS
• To find the difference between means and
proportions of normal at two places or in
different periods.
• Eg : The mean height of boys in Gujarat is less
than the mean height in Punjab. Whether this
difference is due to chance or a natural
variation or because of some other factors
such as better nutrition playing a part, has to
be decided?

10. • To find the correlation between two
variables X and Y such as height and
weight.
• Eg: Whether weight increases or decreases
proportionately with height and if so by how
much, has to be found?

11. IN MEDICINE
To compare the efficacy of a particular drug,
operation or line of treatment – for this, the
percentage cured, relieved or died in the
experiment and control groups, is compared and
difference due to chance or otherwise is found by
applying statistical techniques.
To find an association between two attributes
such as cancer and smoking or filariasis and
social class
(an appropriate test is applied for this purpose.)

12. • To identify signs and symptoms of a disease or
syndrome.
 Cough in typhoid is found by chance and fever
is found in almost every case.
The proportional incidence of one symptom or
another indicates whether it is a characteristic
feature of the disease or not.
• To test usefulness of sera and vaccines in the
field – percentage of attacks or deaths among
the vaccinated subjects is compared with that
among the unvaccinated ones to find whether
the difference observed is statistically
significant.

13. IN EPIDEMIOLOGICAL STUDIES
• The role of causative factors is statistically
tested.
• Deficiency of iodine as an important cause of
goiter in a community is confirmed only after
comparing the incidence of goiter cases before
and after giving iodized salt.

14. IN MODERN MEDICINE
• For decades, Biostatistics has played an integral role in
modern medicine in everything from analyzing data to
determining if a treatment will work to developing
clinical trials.
• The University of North Carolina's Gillings School of
Global Public Health defines biostatistics as "the
science of obtaining, analyzing and interpreting data
in order to understand and improve human health.”

15. • Most people have heard the statistic that
Heart disease is the leading cause of
death in America today*.
• But how do we know this fact to be true?
• Where did that information come from?

16. • Back in 1948, when a lot wasn't known about the factors
leading to heart disease and stroke, a health research study -
known as the Framingham Heart Study was done on 5,209
people living in the town of Framingham, Mass.
• These participants hadn't developed any known symptoms of
cardiovascular disease and hadn't had a stroke or heart attack.
• The study was landmark in several ways. It showed that
there was no one cause for getting a heart attack, and
combining information about several risk factors could
estimate the risk of someone getting the disease.

17. • Thanks to the Framingham Study, (which is still going on
today), we now know the major risk factors that lead to
cardiovascular disease.
• To reach these conclusions, researchers simply followed the
numbers -- the Biostatistics numbers to be exact.
CLINICALMEDICINE
•Documentation of medical history of diseases.
•Planning and conduct of clinical studies.
•Evaluating the merits of different procedures.
•In providing methods for definition of normal’
and‘abnormal’.

18. INBIOTECHNOLOGY
• Biotechnology can focus on a whole range of
topics, from genetic modification of plants and
animals to gene therapy, medicine and drug
manufacturing, reproductive therapy, and even
energy production.
• In all cases, research is carried out bydeveloping
something and testing whether or not it has the
desired performance.
• Determining performance requiresstatistical
analysis of results.

19. CALCULATE STANDARDNORMALSCORES AND
RESULTING PROBABILITIES

20. Measures of Central Tendency
• Central tendency is also called average.
• This gives us idea about the concentration of
the value in the central part of distribution.

21. Mean(Average)
• It locate the distribution on central.
• Known as arithmetic mean.
• The mean is simply the sum of data set divided
by the number of data set.
• Formula

22. • Merits
1. It is easy to calculate and based upon the
observation.
2. Capable for further mathematical Treatment.
3. Affected by simple fluctuation hence it is more
stable.
• Demerits
1. Mean can not calculate the qualitative data eg.
Color, Sex Gender etc.
2. It can not be calculated if a single value are
missing.

23. • There are two formulae is given for different
types of data sets.

24. • Examples- For ungrouped data sets.
1. Body weights of new born are given below
find out the mean?
3.3 6.1 5.8 3.8 2.7 4.1 3.4 3.9
5.1 3

25. 2. Values of serum uric acid in new born are
given below find out the mean?
9.3 6.1 5.8 3.8 6 4.1 3.4 3.9
5.1 6.6

26. Examples. For Grouped Data sets

27. Age Group No. of
students(f)
Find Mean of
age group=X
F,X=
10-15 10 10+15/2=
12.5
125
15-20 4 15+20/2=
17.5
70
20-25 5 20+25/2=
22.5
112.5
25-30 7 25+30/2=
27.5
192.5
26 500
MEAN=500/26=19.23

28. • Example. Find the days of confinement after
the normal delivery of women?
• 321/40=8
• Answer will 7.61
Days of confinement No. of patients
5 7*5=35
6 8*6=48
7 3*7=21
8 5*8=40
9 7*9=63
10 3*10=30
12 7*12=84
f=40

55. Boys Girls
Frederick 70 Grace 82
Russel 95 Irish 80
Murphy 60 Abigail 83
Jerome 80 Sherry 81
Tom 100 Kristine 79
Mean: 81 Mean: 81
Scores of 5 Boys and 5 Girls in
Mathematics

56. Boys
60 70 80 90 100
Girls
60 70 80 90 100

57. Measures of Variability or
Dispersion

58. RANGE:
The difference between the highest and the
lowest observation
R = H – L
Boys:
Girls:
R = 100 – 60
R = 40
R = 83 – 79
R = 4
Therefore the
girls are more
homogeneous
than the boys in
their math
ability

59. Mean Deviation:
The average of the summation of the
absolute deviation of each observation
from the mean.
MD = Σ Xi - X
n

60. BOYS Xi Xi – X
Frederick 70 11
Russel 95 14
Murphy 60 21
Jerome 80 1
Tom 100 19
Mean: 81 Σ = 405 Σ = 66
M.D = 66 / 5
= 13.2

61. GIRLS Xi Xi – X
Grace 82 1
Irish 80 1
Abigail 83 2
Sherry 81 0
Kristine 79 2
Mean: 81 Σ = 405 Σ = 6
M.D = 6 / 5
= 1.2

62. MD ( boys ) = 13.2
MD ( girls ) = 1.2
- based from the computed Mean
Deviation, the girls are more
homogeneous than the boys.

63. VARIANCE:
The average of the squared deviation from
the mean.
Population Variance
σ 2
= Σ ( Xi – X ) 2
n
Sample Variance
s 2
= Σ ( Xi – X ) 2
n - 1

64. BOYS Xi Xi – X ( Xi – X ) 2
Frederick 70 -11 121
Russel 95 14 196
Murphy 60 -21 441
Jerome 80 -1 1
Tom
Mean: 81
100
Σ = 405
19 361
Σ = 1,120
σ2 = 1,120 / 5
= 224
s2 = 1,120 / 4
= 280

65. GIRLS Xi Xi – X ( Xi – X ) 2
Grace 82 1 1
Irish 80 1 1
Abigail 83 2 4
Sherry 81 0 0
Kristine 79 2 4
Σ = 10
σ2 = 10 / 5
Mean: 81 Σ = 405
= 2
s2 = 10 / 4
= 2.5

66. BOYS
σ2= 1,120 / 5
= 224
s2= 1,120 / 4
= 280
GIRLS
σ2 = 10 / 5
= 2
s2 = 10 / 4
= 2.5
The values of
the Variance
also reveals that
the score of
boys are more
spread out than
that of the girls.

67. STANDARD DEVIATION:
The square root of the Variance
BOYS
σ 2 = 224 s 2= 280
σ = 14.97 s = 16.73
σ 2= 2
GIRLS
s 2= 2.5
σ = 1.41 s = 1.58

68. Question
:
Why do you think the
RANGE is considered an
unreliable Measure of
Variability?

69. Answer:
The RANGE is considered
unreliable because we will only
use two values, the highest and the
lowest which is not a complete
representation of all the
observations.

70. SEATWORK:
Given the table below, compute for R,
MD, s, and s2
Xi l Xi – X l ( Xi – X ) 2
17
15
22
19
18
Σ = Σ = Σ =

71. Xi l Xi – X l ( Xi – X ) 2
17 1.2 1.44
15 3.2 10.24
22 3.8 14.44
19 0.8 0.64
18 0.2 0.04
Σ = 91 Σ = 9.2 Σ = 26.8

72. 1. Range = 7
2. MD = 1.84
3. s = 2.59
σ = 2.32
4. s 2 = 6.7
σ 2 = 5.36