Downloaded 10 times
Uploaded byAchmad Solichin
Binary Search Tree (BST) - Algoritma dan Struktur Data
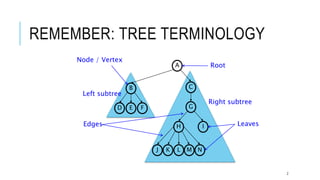
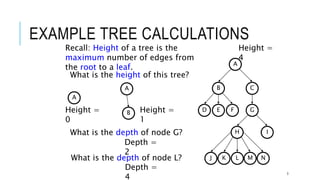
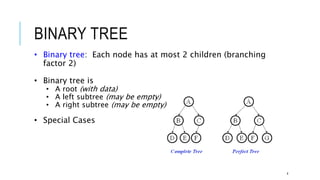
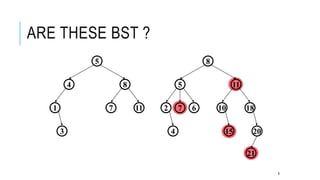
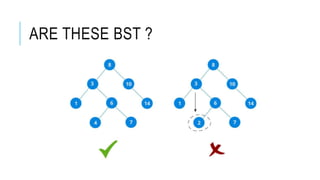
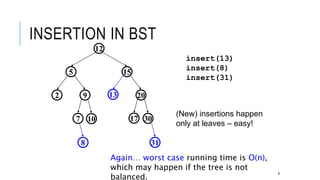
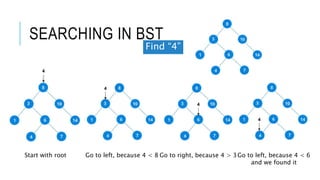
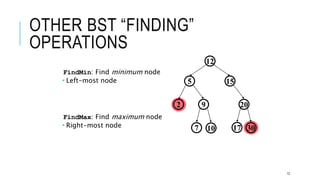
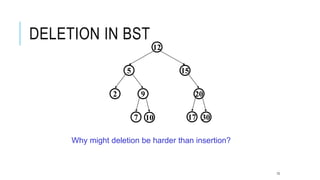
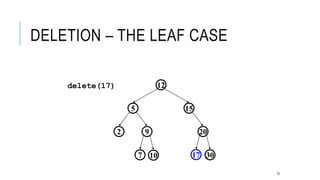
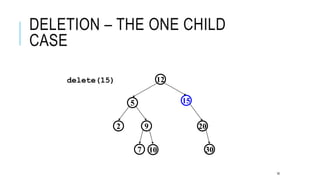
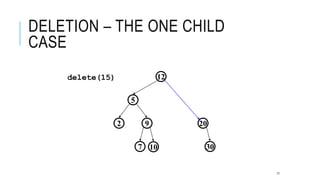
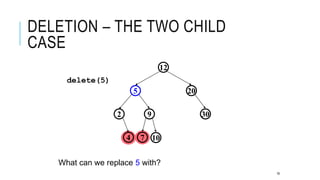
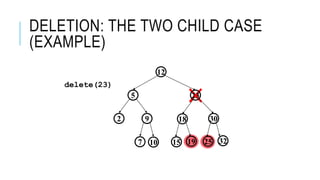
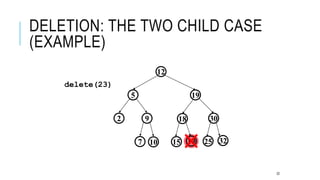
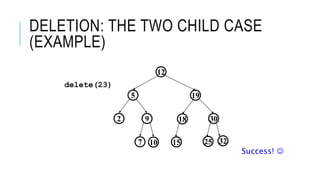
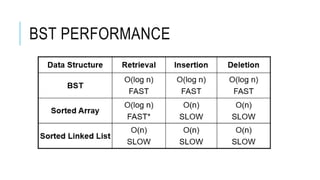
The document explains the binary search tree (BST) algorithm and data structure, detailing key concepts like tree terminology, properties of binary trees, and specific operations such as insertion, searching, and deletion in BSTs. It highlights the challenges of deletion compared to insertion and provides algorithms for managing different cases during deletions. The content is supported by references to academic slides and external resources.
More Related Content
Similar to Binary Search Tree (BST) - Algoritma dan Struktur Data
Binary Search Tree (BST) - Algoritma dan Struktur Data
- 1. BINARY SEARCH TREE (BST) Algoritmadan Struktur Data Dr. Achmad Solichin, S.Kom, M.T.I
- 2. REMEMBER: TREE TERMINOLOGY 2 A E B DF C G IH LJ MK N Node / Vertex Edges Root Leaves Left subtree Right subtree
- 3. EXAMPLE TREE CALCULATIONS 3 A E B DF C G IH LJ MK N A Recall: Height of a tree is the maximum number of edges from the root to a leaf. Height = 0 A B Height = 1 What is the height of this tree? What is the depth of node G? What is the depth of node L? Depth = 2 Depth = 4 Height = 4
- 4. BINARY TREE 4 • Binarytree: Each node has at most 2 children (branching factor 2) • Binary tree is • A root (with data) • A left subtree (may be empty) • A right subtree (may be empty) • Special Cases
- 5. BINARY SEARCH TREE(BST) DATA STRUCTURE 4 121062 115 8 14 13 7 9 Structure property (binary tree) Each node has 2 children Result: keeps operations simple Order property All keys in left subtree smaller than node’s key All keys in right subtree larger than node’s key Result: easy to find any given key 5 A binary search tree is a type of binary tree (but not all binary trees are binary search trees!)
- 6. ARE THESE BST? 3 1171 84 5 4 181062 115 8 20 21 7 15 6
- 7.
- 8. INSERTION IN BST 2092 155 12 30717 insert(13) insert(8) insert(31) (New) insertions happen only at leaves – easy! 10 8 31 13 8 Again… worst case running time is O(n), which may happen if the tree is not balanced.
- 9.
- 10. SEARCHING IN BST Find“4” ! Start with root Go to left, because 4 < 8 Go to right, because 4 > 3Go to left, because 4 < 6 and we found it
- 11. SEARCHING IN BST:ALGORITHM
- 12. OTHER BST “FINDING” OPERATIONS FindMin:Find minimum node Left-most node FindMax: Find maximum node Right-most node 2092 155 12 307 1710 12
- 13. DELETION IN BST 2092 155 12 30717 Why might deletion be harder than insertion? 10 13
- 14. DELETION IN BST Basicidea: find the node to be removed, then “fix” the tree so that it is still a binary search tree Three potential cases to fix: Node has no children (leaf) Node has one child Node has two children 14
- 15. DELETION – THELEAF CASE 2092 155 12 307 17 delete(17) 10 15
- 16. DELETION – THEONE CHILD CASE 2092 155 12 307 10 16 delete(15)
- 17. DELETION – THEONE CHILD CASE 2092 5 12 307 10 17 delete(15)
- 18. DELETION – THETWO CHILD CASE 3092 205 12 7 What can we replace 5 with? 10 18 delete(5) 4
- 19. DELETION – THETWO CHILD CASE What can we replace the node with? Options: successor minimum node from right subtree findMin(node.right) predecessor maximum node from left subtree findMax(node.left) 19
- 20. DELETION: THE TWOCHILD CASE (EXAMPLE) 3092 235 12 7 10 18 1915 3225 delete(23)
- 21. DELETION: THE TWOCHILD CASE (EXAMPLE) 3092 235 12 7 10 18 1915 3225 delete(23)
- 22. DELETION: THE TWOCHILD CASE (EXAMPLE) 22 3092 195 12 7 10 18 1915 3225 delete(23)
- 23. DELETION: THE TWOCHILD CASE (EXAMPLE) 3092 195 12 7 10 18 15 3225 Success! delete(23)
- 24.
- 25.
- 26. REFERENSI Slide byLauren Milne, entitled “Lecture 6: Binary Search Trees”, University of Washington Slide from King Abdulaziz University, entitled “Binary Search Tree”. https://www.programiz.com/dsa/binary-search-tree https://en.wikipedia.org/wiki/Binary_search_tree
- 27. THANK YOU Dr. AchmadSolichin, S.Kom. M.T.I. Universitas Budi Luhur achmad.solichin@budiluhur.ac.id | http://achmatim.net