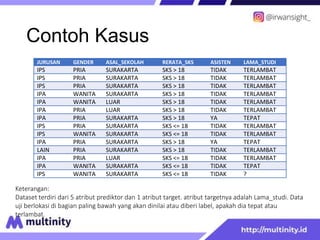
The document discusses the Naive Bayes classifier. It begins with an introduction to probability and defines the formula for Naive Bayes classification. It then provides an example dataset to demonstrate how to calculate the probabilities of each attribute value belonging to each class. The example shows calculating the probabilities for attributes like major, gender, school origin, GPA, and assistant status to predict whether a student's study duration will be on time or late.

1. Naïve Bayes Classifier
Irwansyah Saputra, S.Kom., M.Kom., MTA
Founder of Multinity Indonesia

2. Tentang Saya
• Irwansyah Saputra
• Dosen Ilmu Komputer
• Mahasiswa S3 Ilmu Komputer IPB University
• Bidang Kajian: Computational Intelligence &
Optimization (Data mining, machine
learning, artificial intelligence)
Halo semuanya, saya suka belajar tentang
segala hal dan suka berbagi pengetahuan. Saya
juga sering menjadi pembicara di berbagai
seminar.
Kontak yang bisa dihubungi:
WhatsApp: 0895323302241
Instagram: @irwansight_
Web: https://irw.one

3. Disclaimer
Materi ini digunakan sebagai bahan ajar Program Data Mining di
Multinity.id
Silakan gunakan, mohon untuk tidak mengubah template.
Jika Anda memiliki kesulitan dalam memahami materi pada slide
ini, silakan belajar di Multinity.id

4. Referensi
1. Jiawei Han and Micheline Kamber, Data Mining: Concepts and Techniques Third
Edition, Elsevier, 2012
2. Ian H. Witten, Frank Eibe, Mark A. Hall, Data mining: Practical Machine Learning
Tools and Techniques 3rd Edition, Elsevier, 2011
3. Markus Hofmann and Ralf Klinkenberg, RapidMiner: Data Mining Use Cases and
Business Analytics Applications, CRC Press Taylor & Francis Group, 2014
4. Daniel T. Larose, Discovering Knowledge in Data: an Introduction to Data Mining,
John Wiley & Sons, 2005
5. Ethem Alpaydin, Introduction to Machine Learning, 3rd ed., MIT Press, 2014
6. Florin Gorunescu, Data Mining: Concepts, Models and Techniques, Springer,
2011
7. Oded Maimon and Lior Rokach, Data Mining and Knowledge Discovery Handbook
Second Edition, Springer, 2010
8. Warren Liao and Evangelos Triantaphyllou (eds.), Recent Advances in Data Mining
of Enterprise Data: Algorithms and Applications, World Scientific, 2007
9. Suyanto, DATA MINING: Untuk klasifikasi dan klasterisasi data, Penerbit
Informatika, 2017

5. Naïve Bayes Classifier
• Naïve bayes mengandalkan probabilitas dari record.
• Probabilitas/peluang yang paling mudah dijadikan contoh kasus
adalah dadu.
• Berapa peluang munculnya angka 4 dalam satu kali lemparan?
1/6
Berasal dari kemungkinan
angka 4 muncul dalam satu
kali lemparan
Berasal dari total angka
yang terdapat pada dadu

6. Naïve Bayes Classifier
• Rumus umumnya adalah sebagai berikut:
𝑃 𝑐 𝑋 =
𝑃 𝑥 𝑐 𝑃(𝑐)
𝑃(𝑥)
Keterangan:
𝑋 : Data dengan class yang belum diketahui
𝑐 : Hipotesis data merupakan suatu class spesifik
𝑃 𝑐 𝑋 : Probabilitas hipotesis berdasar kondisi (posteriori probability)
𝑃(𝑐) : Probabilitas hipotesis (prior probability)
𝑃 𝑥 𝑐 : Probabilitas berdasarkan kondisi pada hipotesis
𝑃(𝑥) : Probabilitas c
• Rumus NBC adalah:
𝑃 𝑐 𝑋 = 𝑃 𝑥𝑖 𝑐 ∗ 𝑃(𝑐)

7. Contoh Kasus
JURUSAN GENDER ASAL_SEKOLAH RERATA_SKS ASISTEN LAMA_STUDI
IPS PRIA SURAKARTA SKS > 18 TIDAK TERLAMBAT
IPS PRIA SURAKARTA SKS > 18 TIDAK TERLAMBAT
IPS PRIA SURAKARTA SKS > 18 TIDAK TERLAMBAT
IPA WANITA SURAKARTA SKS > 18 TIDAK TERLAMBAT
IPA WANITA LUAR SKS > 18 TIDAK TERLAMBAT
IPA PRIA LUAR SKS > 18 TIDAK TERLAMBAT
IPA PRIA SURAKARTA SKS > 18 YA TEPAT
IPS PRIA SURAKARTA SKS <= 18 TIDAK TERLAMBAT
IPS WANITA SURAKARTA SKS <= 18 TIDAK TERLAMBAT
IPA PRIA SURAKARTA SKS > 18 YA TEPAT
LAIN PRIA SURAKARTA SKS > 18 TIDAK TERLAMBAT
IPA PRIA LUAR SKS <= 18 TIDAK TERLAMBAT
IPA WANITA SURAKARTA SKS <= 18 TIDAK TEPAT
IPS WANITA SURAKARTA SKS <= 18 TIDAK ?
Keterangan:
Dataset terdiri dari 5 atribut prediktor dan 1 atribut target. atribut targetnya adalah Lama_studi. Data
uji berlokasi di bagian paling bawah yang akan dinilai atau diberi label, apakah dia tepat atau
terlambat.

8. Penyelesaian
• Menentukan P(Ci) terlebih dahulu dengan cara menghitung kategori kelas pada target
berdasarkan jumlah keseluruhannya.
• Karena kategori kelas pada target hanya ada dua yaitu “Tepat” dan “Terlambat” maka
hasilnya menjadi:
𝑃 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 𝑡𝑒𝑟𝑙𝑎𝑚𝑏𝑎𝑡) =
10
13
= 0.83
𝑃 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 𝑡𝑒𝑝𝑎𝑡) =
3
13
= 0.23
• Selanjutnya, hitung juga P(X|ci) dari setiap atribut yang ada. Maksudnya adalah
menghitung berbagai kelas dari setiap atribut. Sebagai contoh:
𝑃 𝑗𝑢𝑟𝑢𝑠𝑎𝑛 = 𝐼𝑃𝐴 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑝𝑎𝑡) =
3
3
= 1
Keterangan:
Angka 3 yang atas adalah jumlah jurusan IPA yang memiliki lama studinya tepat. Angka 3 yang
bawah adalah jumlah lama studi = tepat yang ada di atribut target.

9. Penyelesaian
• Hitung atribut lainnya sehingga menjadi:
atribut Perhitungan
Jurusan
𝑃 𝑗𝑢𝑟𝑢𝑠𝑎𝑛 = 𝐼𝑃𝐴 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑝𝑎𝑡) =
3
3
= 1
𝑃 𝑗𝑢𝑟𝑢𝑠𝑎𝑛 = 𝐼𝑃𝑆 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑝𝑎𝑡) =
0
3
= 0
𝑃 𝑗𝑢𝑟𝑢𝑠𝑎𝑛 = 𝐿𝑎𝑖𝑛 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑝𝑎𝑡) =
0
3
= 0
𝑃 𝑗𝑢𝑟𝑢𝑠𝑎𝑛 = 𝐼𝑃𝐴 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑟𝑙𝑎𝑚𝑏𝑎𝑡) =
4
10
= 0.4
𝑃 𝑗𝑢𝑟𝑢𝑠𝑎𝑛 = 𝐼𝑃𝑆 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑟𝑙𝑎𝑚𝑏𝑎𝑡) =
5
10
= 0.5
𝑃 𝑗𝑢𝑟𝑢𝑠𝑎𝑛 = 𝐿𝑎𝑖𝑛 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑟𝑙𝑎𝑚𝑏𝑎𝑡) =
1
10
= 0.1
Gender
𝑃 𝐺𝑒𝑛𝑑𝑒𝑟 = 𝑃𝑟𝑖𝑎 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑝𝑎𝑡) =
2
3
= 0.67
𝑃 𝐺𝑒𝑛𝑑𝑒𝑟 = 𝑊𝑎𝑛𝑖𝑡𝑎 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑝𝑎𝑡) =
1
3
= 0.33
𝑃 𝐺𝑒𝑛𝑑𝑒𝑟 = 𝑃𝑟𝑖𝑎 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑟𝑙𝑎𝑚𝑏𝑎𝑡) =
7
10
= 0.7
𝑃 𝐺𝑒𝑛𝑑𝑒𝑟 = 𝑊𝑎𝑛𝑖𝑡𝑎 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑟𝑙𝑎𝑚𝑏𝑎𝑡) =
3
10
= 0.3

10. Penyelesaian
atribut Perhitungan
Asal_Sekolah
𝑃 𝐴𝑠𝑎𝑙𝑆𝑒𝑘𝑜𝑙𝑎ℎ = 𝑆𝑢𝑟𝑎𝑘𝑎𝑟𝑡𝑎 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑝𝑎𝑡) =
3
3
= 1
𝑃 𝐴𝑠𝑎𝑙𝑆𝑒𝑘𝑜𝑙𝑎ℎ = 𝐿𝑢𝑎𝑟 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑝𝑎𝑡) =
0
3
= 0
𝑃 𝐴𝑠𝑎𝑙𝑆𝑒𝑘𝑜𝑙𝑎ℎ = 𝑆𝑢𝑟𝑎𝑘𝑎𝑟𝑡𝑎 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑟𝑙𝑎𝑚𝑏𝑎𝑡) =
7
10
= 0.7
𝑃 𝐴𝑠𝑎𝑙𝑆𝑒𝑘𝑜𝑙𝑎ℎ = 𝐿𝑢𝑎𝑟 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑟𝑙𝑎𝑚𝑏𝑎𝑡) =
3
10
= 0.3
Rerata_SKS
𝑃 𝑅𝑒𝑟𝑎𝑡𝑎𝑆𝐾𝑆 = 𝑆𝐾𝑆 > 18 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑝𝑎𝑡) =
2
3
= 0.67
𝑃 𝑅𝑒𝑟𝑎𝑡𝑎𝑆𝐾𝑆 = 𝑆𝐾𝑆 ≤ 18 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑝𝑎𝑡) =
1
3
= 0.33
𝑃 𝑅𝑒𝑟𝑎𝑡𝑎𝑆𝐾𝑆 = 𝑆𝐾𝑆 > 18 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑟𝑙𝑎𝑚𝑏𝑎𝑡) =
7
10
= 0.7
𝑃 𝑅𝑒𝑟𝑎𝑡𝑎𝑆𝐾𝑆 = 𝑆𝐾𝑆 ≤ 18 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑟𝑙𝑎𝑚𝑏𝑎𝑡) =
3
10
= 0.3
Asisten
𝑃 𝐴𝑠𝑖𝑠𝑡𝑒𝑛 = 𝑌𝑎 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑝𝑎𝑡) =
2
3
= 0.67
𝑃 𝐴𝑠𝑖𝑠𝑡𝑒𝑛 = 𝑇𝑖𝑑𝑎𝑘 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑝𝑎𝑡) =
1
3
= 0.33
𝑃 𝐴𝑠𝑖𝑠𝑡𝑒𝑛 = 𝑌𝑎 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑟𝑙𝑎𝑚𝑏𝑎𝑡) =
0
10
= 0
𝑃 𝐴𝑠𝑖𝑠𝑡𝑒𝑛 = 𝑇𝑖𝑑𝑎𝑘 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑇𝑒𝑟𝑙𝑎𝑚𝑏𝑎𝑡) =
10
10
= 1

11. Penyelesaian
• Setelah perhitungan probabilitas tiap atribut selesai, maka langkah selanjutnya adalah
menghitung nilai target untuk data uji yang sudah disiapkan yaitu:
• Maka kita kalikan sesuai dengan kategori data uji, hasilnya adalah:
𝑃 𝑋 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑡𝑒𝑝𝑎𝑡 ∗ 𝑃 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑡𝑒𝑝𝑎𝑡
=
0
3
𝑥
1
3
𝑥
3
3
𝑥
1
3
𝑥
1
3
𝑥
3
13
= 0
𝑃 𝑋 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑡𝑒𝑟𝑙𝑎𝑚𝑏𝑎𝑡 ∗ 𝑃 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑡𝑒𝑟𝑙𝑎𝑚𝑏𝑎𝑡
=
5
10
𝑥
3
10
𝑥
7
10
𝑥
3
10
𝑥
10
10
𝑥
10
13
= 0.024
• Karena nilai kelas LamaStudi = terlambat lebih tinggi dibandingkan kelas tepat, maka data
uji akan bernilai terlambat. Perhitungan NBC selesai sampai di sini.
IPS WANITA SURAKARTA SKS <= 18 TIDAK

12. Laplacian Correction
Irwansyah Saputra, S.Kom., M.Kom., MTA
Founder of Multinity Indonesia

13. Apa itu laplacian correction?
• Teknik perhitungan yang mampu menghindari probabilitas bernilai 0
• Disebut juga dengan laplace estimator
• Ditemukan oleh Pierre Laplace ahli matematika Perancis abad ke-18
• Untuk dataset yang memiliki jumlah tupel sedikit, teknik ini kurang
akurat.
• Sangat akurat untuk digunakan pada dataset yang jumlah tupelnya
banyak.

14. Laplacian Correction
• Perhatikan hitungan sebelumnya:
𝑃 𝑋 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑡𝑒𝑝𝑎𝑡 ∗ 𝑃 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑡𝑒𝑝𝑎𝑡
=
0
3
𝑥
1
3
𝑥
3
3
𝑥
1
3
𝑥
1
3
𝑥
3
13
= 0
• Pada bagian ini, terdapat nilai 0 sehingga seluruh perkalian hasilnya menjadi 0.
• ini dirasa tidak adil karena hanya disebabkan satu atribut yang 0, maka seluruhnya jadi 0.
• Itulah kenapa laplacian correction hadir. Untuk membangkitkan nilai 0 sehingga hasil
perhitungannya tidak sama dengan 0.

15. Cara Kerja Laplacian Correction
• Menambahkan satu tupel pura-pura dengan kelas Lama Studi = Tepat.
Kenapa? Karena probabilitas yang memiliki nilai 0 adalah Lama Studi = Tepat.
• Ada 5 atribut yaitu Jurusan = IPS, Gender = Wanita, Asal Sekolah = Surakarta,
Rerata SKS = SKS <= 18, Asisten = Tidak. Sehingga tupel yang ditambahkan
adalah 5.
• Perlu diingat, tupel yang kita buat ini adalah tupel pura-pura, cukup untuk
dibayangkan saja. Hanya untuk menghindari probabilitas 0.

16. Penyelesaian
• Perhatikan hitungan sebelumnya:
𝑃 𝑋 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑡𝑒𝑝𝑎𝑡 ∗ 𝑃 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑡𝑒𝑝𝑎𝑡
=
0
3
𝑥
1
3
𝑥
3
3
𝑥
1
3
𝑥
1
3
𝑥
3
13
= 0
• Setelah digunakan Laplacian Correction menjadi:
𝑃 𝑋 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑡𝑒𝑝𝑎𝑡 ∗ 𝑃 𝐿𝑎𝑚𝑎𝑆𝑡𝑢𝑑𝑖 = 𝑡𝑒𝑝𝑎𝑡
=
1
8
𝑥
2
8
𝑥
4
8
𝑥
2
8
𝑥
2
8
𝑥
3
13
= 0.000225361
• Walaupun nilainya tetap lebih kecil, namun ada perubahan yang signifikan dari nilai 0
menjadi tidak 0.
• Teknik Laplacian correction ini akan sangat berguna pada dataset yang berukuran sangat
besar.