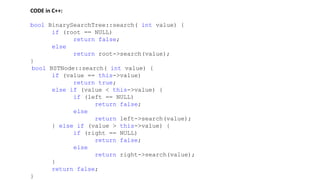
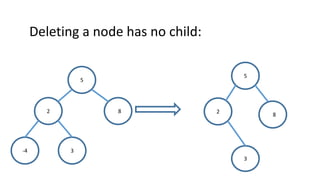
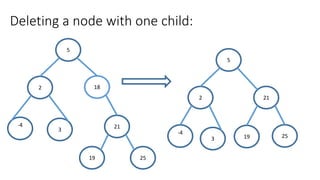
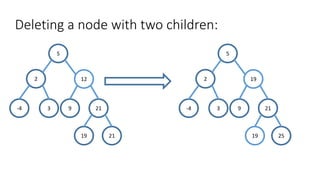
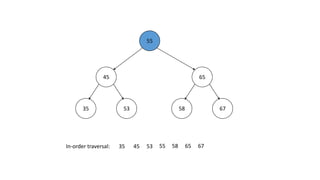
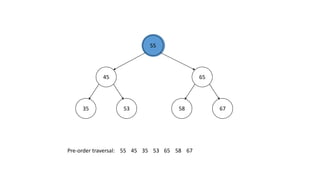
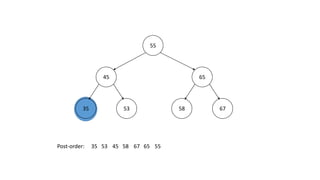
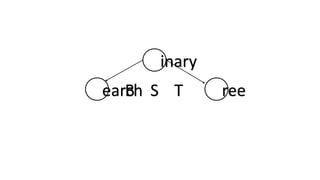
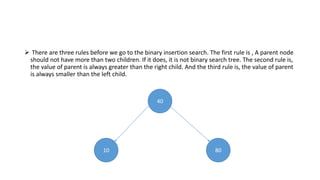
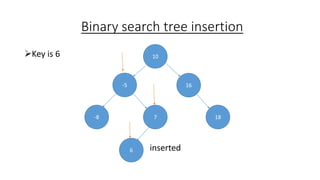
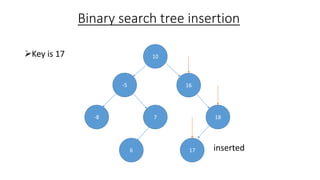
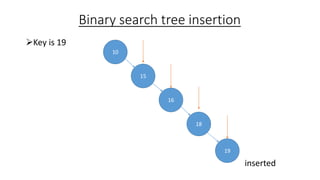
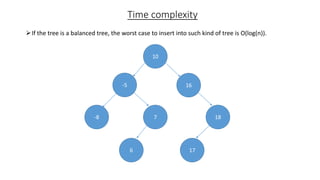
The document outlines the definition and operations of binary search trees (BST), including insertion, search, deletion, and traversal methods. It describes the rules for maintaining a BST and provides time complexity for various operations, indicating that searching and inserting in a balanced tree has an average complexity of O(log n). Additionally, it offers real-life applications and references for further reading.

1. Welcome

2. Binary Search treeInsertion, Search and Deletion operation and BST sort

3. Team Members
Israt Jahan Fateha (151-15-5036)
Md. Eyakub Sorkar (151-15-4674)
Mehedi Imam Shafi (151-15-5248)
Sajiya (151-15-5256)
Sanjida Tasnim (143-15-4397)

4. B S T
inary
earch ree

5. Condition for a binary tree to be a BST
Left child is smaller than parent
Right child is greater than parent

6. 55
45 65
58 675335
Example of binary search tree

7. Basic Operations
• Insertion
• Search
• Deletion
• Traversal
• Sort

8. Insertion

9.  There are three rules before we go to the binary insertion search. The first rule is , A parent node
should not have more than two children. If it does, it is not binary search tree. The second rule is,
the value of parent is always greater than the right child. And the third rule is, the value of parent
is always smaller than the left child.
40
8010

10. Binary search tree insertion
Key is 6
inserted
10
-5 16
-8 7 18
6

11. Binary search tree insertion
Key is 17
inserted
10
-5 16
-8 7 18
6 17

12. Binary search tree insertion
Key is 19
inserted
10
15
16
18
19

13. Time complexity
How much time doe it take to insertion into binary search tree. The worst case, the time it takes
to insert into binary search tree is O(n). Its possible all the nodes have just one child and they are
linear like this one and the worst case here will be O(n).
10
15
16
18
19

14. Time complexity
If the tree is a balanced tree, the worst case to insert into such kind of tree is O(log(n)).
10
-5 16
-8 7 18
6 17

15. Search

16. What will we search?

17. How to search?

18. 65
9
-4 5
4
5 is less than 6
go to the left child
5 is more than 4
go to the right child
Searched value has
been found

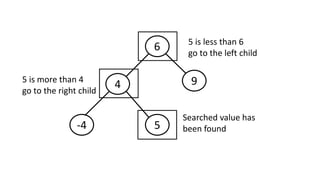
19. Algorithm:
Here k is the key that is searched for and x is the start
node.
BST-Search(x, k)
1. y ← x
2. while y ≠ nil do
3. if key[y] = k then return y
4. else if key[y] < k then y ← right[y]
5. else y ← left[y]
6. return (“NOT FOUND”)

20. CODE in C++:
bool BinarySearchTree::search( int value) {
if (root == NULL)
return false;
else
return root->search(value);
}
bool BSTNode::search( int value) {
if (value == this->value)
return true;
else if (value < this->value) {
if (left == NULL)
return false;
else
return left->search(value);
} else if (value > this->value) {
if (right == NULL)
return false;
else
return right->search(value);
}
return false;
}

21. Time Complexity of Searching in
Binary Search Tree
O( log(n) )O(n)

22. Deletion

23. Deleting a node has no child:
5
182
-4 3
5
18
2
3

24. Deleting a node with one child:
5
-4
2
25
18
21
19
3
5
-4
2
19
21
253

25. Deleting a node with two children:
5
9
12
19
213-4
2
21
5
9
19
213-4
2
2519

26. Sort

27. Already sorted during the step of insertion

28. TraversalPre-order In-order Post-order

29. In-order

30. 55
45 65
58 675335
In-order traversal: 35 45 53 55 58 65 67

31. Pre-Order

32. 55
45 65
58 675335
Pre-order traversal: 55 45 35 53 65 58 67

33. Post-Order

34. 55
45 65
58 675335
Post-order: 35 53 45 58 67 65 55

35. Real Life Use of Binary Search Tree

36. 10,000,0007log(10000000)

37. Maintaining a huge library

38. Game Objects

39. References:
1. http://en.wikipedia.org/binary=search-tree/
2. http://geeksourceforge.com/bst-basic
3. http://github.com/cpp@master/binary-tree/bst.cpp
4. https://www.quora.com/What-are-the-real-world-examples-of-binary-trees-not-search-tree
5. http://www.geeksforgeeks.org/618/

40. Thank You all
For being with us.