Download as PDF, PPTX
Uploaded byBigMine
Exact Data Reduction for Big Data by Jieping Ye
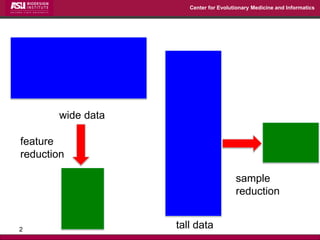
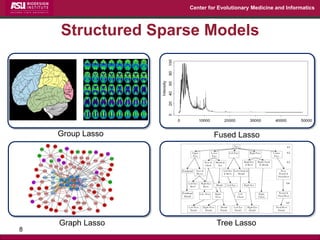
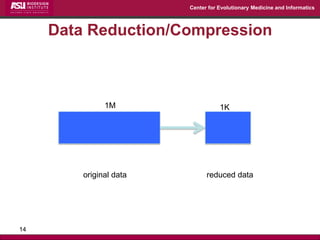
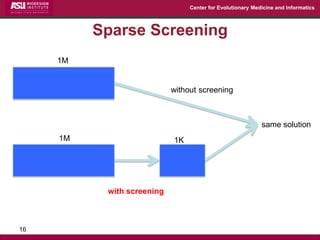
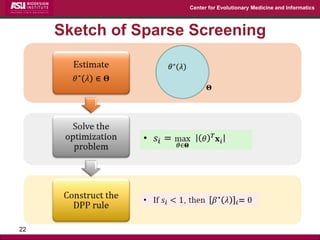
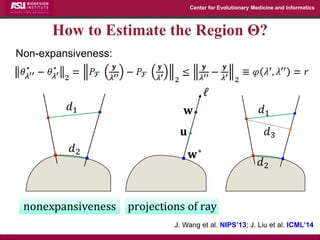
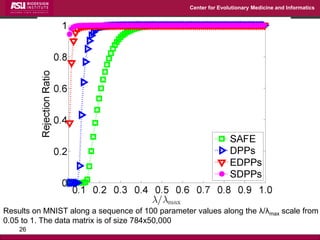
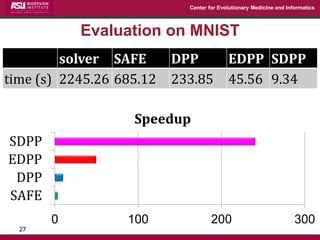
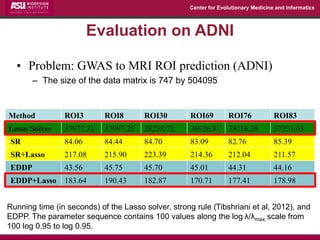
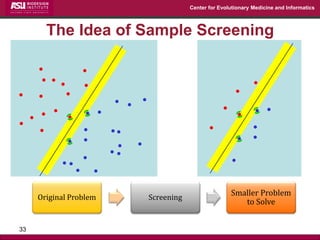
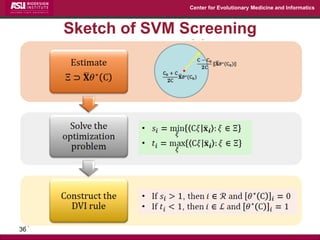
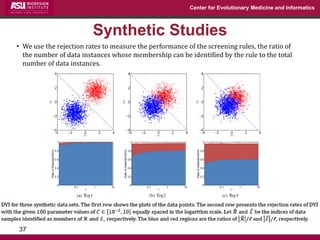
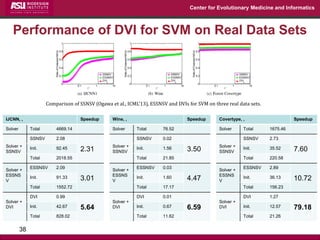
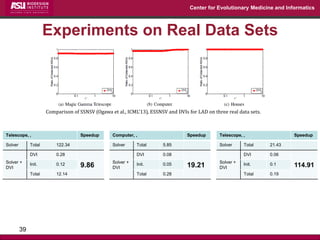
The document discusses the development of exact data reduction techniques using sparse screening methods for both feature and sample reduction, specifically through lasso and support vector machines (SVM). It highlights the efficiency of these approaches in maintaining model integrity while significantly speeding up processing times. Additionally, the document presents various optimization algorithms and extensions of sparse screening to broader applications in machine learning and data science.
Exact Data Reduction for Big Data by Jieping Ye
- 1. Center for EvolutionaryMedicine and Informatics Sparse Screening for Exact Data Reduction Jieping Ye Arizona State University 1 Joint work with Jie Wang and Jun Liu
- 2. Center for EvolutionaryMedicine and Informatics 2 wide data tall data sample reduction feature reduction
- 3. Center for EvolutionaryMedicine and Informatics The model learnt from the reduced data is identical to the model learnt from the full data. We focus on two models in this talk: Lasso for wide data (feature reduction) SVM for tall data (sample reduction) 3 Sparse Screening: A New Framework for Exact Data Reduction
- 4. Center for EvolutionaryMedicine and Informatics 4
- 5. Center for EvolutionaryMedicine and Informatics Lasso/Basis Pursuit (Tibshirani, 1996, Chen, Donoho, and Saunders, 1999) … = × + y A z n×1 n×p n×1 p×1 x 5 Simultaneous feature selection and regression
- 6. Center for EvolutionaryMedicine and Informatics Imaging Genetics (Thompson et al. 2013) 6
- 7. Center for EvolutionaryMedicine and Informatics Sparse Reduced-Rank Regression 7 Vounou et al. (2010, 2012)
- 8. Center for EvolutionaryMedicine and Informatics Structured Sparse Models 8 Group Lasso Tree Lasso Fused Lasso Graph Lasso
- 9. Center for EvolutionaryMedicine and Informatics 9 Sparsity has become an important modeling tool in genomics, genetics, signal and audio processing, image processing, neuroscience (theory of sparse coding), machine learning, statistics …
- 10. Center for EvolutionaryMedicine and Informatics Optimization Algorithms •Coordinate descent •Subgradient descent •Augmented Lagrangian Method •Gradient descent •Accelerated gradient descent •… 10 min loss(x) + λ×penalty(x)
- 11. Center for EvolutionaryMedicine and Informatics Lasso Fused Lasso Group Lasso Sparse Group Lasso Tree Structured Group Lasso Overlapping Group Lasso Sparse Inverse Covariance Estimation Trace Norm Minimization http://www.public.asu.edu/~jye02/Software/SLEP/ 11
- 12. Center for EvolutionaryMedicine and Informatics More Efficiency? 12 Very high dimensional data Non-smooth sparsity-induced norms Multiple runs in model selection A large number of runs in permutation test
- 13. Center for EvolutionaryMedicine and Informatics How to make any existing Lasso solver much more efficient? 13
- 14. Center for EvolutionaryMedicine and Informatics 14 1M 1K Data Reduction/Compression original data reduced data
- 15. Center for EvolutionaryMedicine and Informatics Data Reduction •Heuristic-based data reduction –Sure screening, random projection/selection –Resulting model is an approximation of the true model •Propose data reduction methods –Exact data reduction via sparse screening •The model based on reduced data is identical to the one constructed from complete data 15
- 16. Center for EvolutionaryMedicine and Informatics 16 with screening same solution 1M 1M 1K without screening Sparse Screening
- 17. Center for EvolutionaryMedicine and Informatics Large-Scale Sparse Screening
- 18. Center for EvolutionaryMedicine and Informatics Screening Rule: Motivation Ghaoui, Viallon, and Rabbani.
- 19. Center for EvolutionaryMedicine and Informatics Large-Scale Sparse Screening (Cont’d)
- 20. Center for EvolutionaryMedicine and Informatics More on the Dual Formulation •Solving the dual formulation is difficult •Providing a good (not exact) estimate of the optimal dual solution is easier • A good estimate of the optimal dual solution is sufficient for effective feature screening 20
- 21. Center for EvolutionaryMedicine and Informatics Screening Rule 21
- 22. Center for EvolutionaryMedicine and Informatics Sketch of Sparse Screening 22
- 23. Center for EvolutionaryMedicine and Informatics How to Estimate the Region Θ? J. Wang et al. NIPS’13; J. Liu et al. ICML’14 Non-expansiveness:
- 24. Center for EvolutionaryMedicine and Informatics Enhanced DPP 24 Use projections of rays: Define: Enhanced DPP:
- 25. Center for EvolutionaryMedicine and Informatics Firmly Non-expansive Projection 25 Non-expansiveness: Firmly non-expansiveness:
- 26. Center for EvolutionaryMedicine and Informatics 26 Results on MNIST along a sequence of 100 parameter values along the λ/λmax scale from 0.05 to 1. The data matrix is of size 784x50,000
- 27. Center for EvolutionaryMedicine and Informatics 27 Evaluation on MNIST solver SAFE DPP EDPP SDPP time (s) 2245.26 685.12 233.85 45.56 9.34 0 100 200 300 SAFE DPP EDPP SDPP Speedup
- 28. Center for EvolutionaryMedicine and Informatics Evaluation on ADNI •Problem: GWAS to MRI ROI prediction (ADNI) –The size of the data matrix is 747 by 504095 Method ROI3 ROI8 ROI30 ROI69 ROI76 ROI83 Lasso Solver 37975.31 37097.25 38258.72 36926.81 38116.29 37251.03 SR 84.06 84.44 84.70 83.09 82.76 85.39 SR+Lasso 217.08 215.90 223.39 214.36 212.04 211.57 EDDP 43.56 45.75 45.70 45.01 44.31 44.16 EDDP+Lasso 183.64 190.43 182.87 170.71 177.41 178.98 Running time (in seconds) of the Lasso solver, strong rule (Tibshriani et al, 2012), and EDPP. The parameter sequence contains 100 values along the log λ/λmax scale from 100 log 0.95 to log 0.95.
- 29. Center for EvolutionaryMedicine and Informatics Sparse Screening Extensions •Group Lasso –J Wang, J Liu, J Ye. Efficient Mixed-Norm Regularization: Algorithms and Safe Screening Methods. arXiv preprint arXiv:1307.4156. •Sparse Logistic Regression –J Wang, J Zhou, P Wonka, J Ye. A Safe Screening Rule for Sparse Logistic Regression. arXiv preprint arXiv:1307.4145. •Sparse Inverse Covariance Estimation –S Huang, J Li, L Sun, J Liu, T Wu, K Chen, A Fleisher, E Reiman, J Ye. Learning brain connectivity of Alzheimer’s disease by exploratory graphical models. NeuroImage 50, 935-949. –Witten, Friedman and Simon (2011), Mazumder and Hastie (2012) •Multiple Graphical Lasso –S Yang, Z Pan, X Shen, P Wonka, J Ye. Fused Multiple Graphical Lasso. arXiv preprint arXiv:1209.2139. 29
- 30. Center for EvolutionaryMedicine and Informatics Wide versus Tall Data 30 wide data tall data
- 31. Center for EvolutionaryMedicine and Informatics Support Vector Machines •SVM is a maximum margin classifier. 31 denotes +1 denotes -1 Margin
- 32. Center for EvolutionaryMedicine and Informatics Support Vectors •SVM is determined by the so-called support vectors. 32 Support Vectors are those data points that the margin pushes up against denotes +1 denotes -1 The non-support vectors are irrelevant to the classifier. Can we make use of this observation?
- 33. Center for EvolutionaryMedicine and Informatics The Idea of Sample Screening 33 Original Problem Screening Smaller Problem to Solve
- 34. Center for EvolutionaryMedicine and Informatics Guidelines for Sample Screening 34 J. Wang, P. Wonka, and J. Ye. ICML’14.
- 35. Center for EvolutionaryMedicine and Informatics Relaxed Guidelines 35
- 36. Center for EvolutionaryMedicine and Informatics Sketch of SVM Screening 36
- 37. Center for EvolutionaryMedicine and Informatics Synthetic Studies 37 •We use the rejection rates to measure the performance of the screening rules, the ratio of the number of data instances whose membership can be identified by the rule to the total number of data instances.
- 38. Center for EvolutionaryMedicine and Informatics Performance of DVI for SVM on Real Data Sets 38 Comparison of SSNSV (Ogawa et al., ICML’13), ESSNSV and DVIs for SVM on three real data sets. IJCNN, , Speedup Solver Total 4669.14 Solver + SSNSV SSNSV 2.08 2.31 Init. 92.45 Total 2018.55 Solver + ESSNSV ESSNSV 2.09 3.01 Init. 91.33 Total 1552.72 Solver + DVI DVI 0.99 5.64 Init. 42.67 Total 828.02 Wine, , Speedup Solver Total 76.52 Solver + SSNSV SSNSV 0.02 3.50 Init. 1.56 Total 21.85 Solver + ESSNSV ESSNSV 0.03 4.47 Init. 1.60 Total 17.17 Solver + DVI DVI 0.01 6.59 Init. 0.67 Total 11.62 Covertype, , Speedup Solver Total 1675.46 Solver + SSNSV SSNSV 2.73 7.60 Init. 35.52 Total 220.58 Solver + ESSNSV ESSNSV 2.89 10.72 Init. 36.13 Total 156.23 Solver + DVI DVI 1.27 79.18 Init. 12.57 Total 21.26
- 39. Center for EvolutionaryMedicine and Informatics Experiments on Real Data Sets 39 Comparison of SSNSV (Ogawa et al., ICML’13), ESSNSV and DVIs for LAD on three real data sets. Telescope, , Speedup Solver Total 122.34 Solver + DVI DVI 0.28 9.86 Init. 0.12 Total 12.14 Computer, , Speedup Solver Total 5.85 Solver + DVI DVI 0.08 19.21 Init. 0.05 Total 0.28 Telescope, , Speedup Solver Total 21.43 Solver + DVI DVI 0.06 114.91 Init. 0.1 Total 0.19
- 40. Center for EvolutionaryMedicine and Informatics Resource 40 •Tutorial webpages of our screening rules, which include sample codes, implementation instructions, illustration materials, etc. http://www.public.asu.edu/~jwang237/screening.html Seven lines implementation of EDPP rule The list is growing quickly
- 41. Center for EvolutionaryMedicine and Informatics Summary •Developed exact data reduction approaches –Exact data reduction via feature screening –Exact data reduction via sample screening •The model based on reduced data is identical to the one constructed from complete data •Results show screening leads to a significant speedup. •Extend exact data reduction to other sparse learning formulations –Sparsity on features, samples, networks etc 41