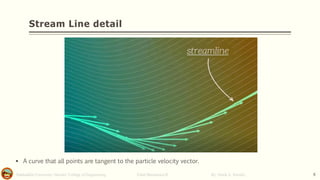
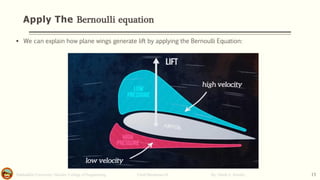
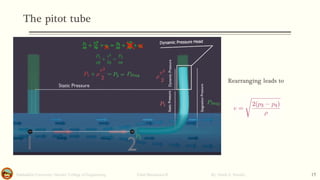
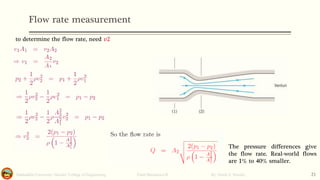
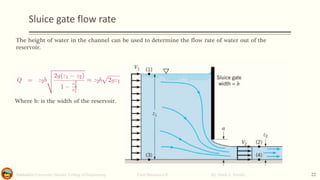
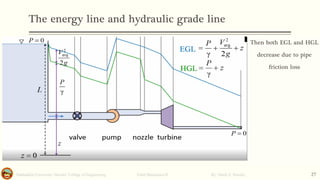
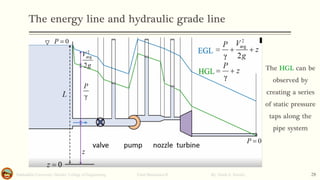
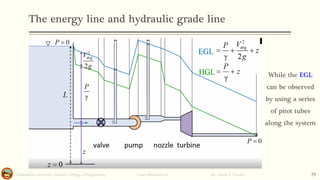
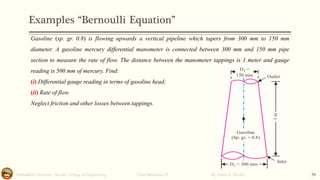
This document discusses Bernoulli's equation and its applications in fluid mechanics. It begins with an introduction to flow patterns such as streamlines and pathlines. It then provides a physical interpretation of Bernoulli's equation relating it to the work-energy principle. Bernoulli's equation states that the sum of pressure, kinetic energy, and potential energy terms remains constant along a streamline. Several examples are provided to demonstrate how Bernoulli's equation can be applied to problems involving pipe flow, venturi meters, and other devices. Stream function, stagnation points, and the hydraulic grade line are also discussed.