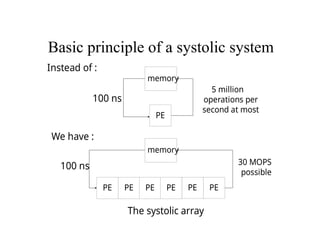
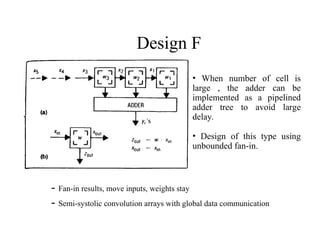
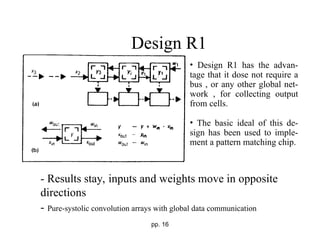
The document discusses systolic architecture as a solution for high-performance, special-purpose computing systems, highlighting its efficiency in mapping computations into hardware structures similar to an assembly line. It outlines key architectural principles, including regular design, concurrency, and the balance between computation and I/O, which contribute to cost-effective and high-performance implementations. Furthermore, it details various convolution designs within systolic systems, emphasizing their mathematical foundations and practical applications in signal processing.




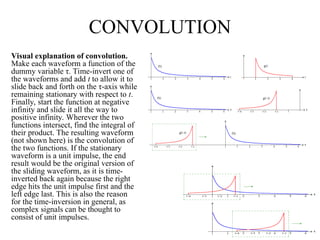

![CONVOLUTION
Code:
#include <stdio.h>
#include <stdlib.h>
int main( ){
int w[ ] = {1,2,2,1};
int x[ ] = { 11,2,3,4,5,6,3,2,1};
int y [20];
int w_len = 4;
int x_len = 9;
int i, j, temp;
for( i=1; i <= (w_len+x_len), i++) {
y[i] = 0;
}
for( i=1; i <= (w_len+x_len - 1); i++) {
for( j =1; j <= w_len; j++){
if ( ( i – j < 0 ) || ( i – j > (x_len -1 ) ) )
temp = 0;
else
temp = x[ i – j];
y[i] = y[i] + w[j] *temp;
}
printf ( “y[ %d] = %d n ” , i , y [i] );
}
return 1;
}](https://image.slidesharecdn.com/convolution-250107052014-a5ac34c1/85/Basic-principle-of-a-systolic-system-Convolution-9-320.jpg)
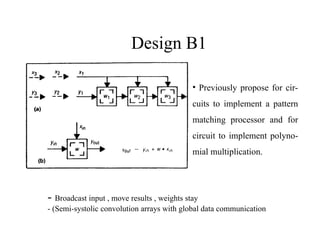

![Design B2
Broadcast input , move weights , results stay
[(Semi-) systolic convolution arrays with
global data communication]
• The path for moving yi’s is
wider then wi’s because of
yi’s carry more bits then wi’s
in numerical accuracy.
• The use of multiplier-
accumlators may also help
increase precision of the
result , since extra bit can be
kept in these accumulators
with modest cost.](https://image.slidesharecdn.com/convolution-250107052014-a5ac34c1/85/Basic-principle-of-a-systolic-system-Convolution-12-320.jpg)



![CONVOLUTION
Description :
For the sequence of computations shown on the previous page, design
a structural VHDL code such that the computation is fully
pipelined. x[i] represents a single datum input to circuit from the
testbench, while y[i] is the output back to the testbench. New
values of x[i] move into the circuit every clock cycle, and new
values of y[i] move out to the testbench every clock cycle.
“Clock” is another input ot the system.
1. The individual components of the system should be described
behaviorally. [25%]
2. Show a plan for architecting your design for a pipelined
implementation. [25%]
3. Write the top level VHDL structural code for the design. [25%]
4. Write a testbench for the system. [25%]](https://image.slidesharecdn.com/convolution-250107052014-a5ac34c1/85/Basic-principle-of-a-systolic-system-Convolution-18-320.jpg)