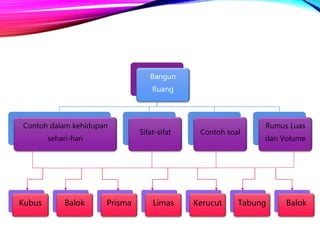
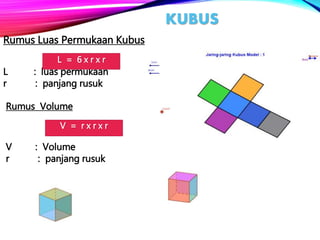
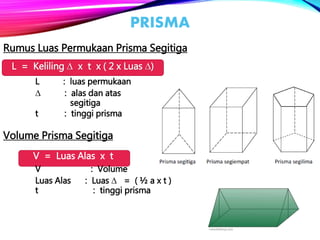
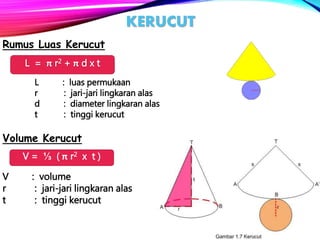
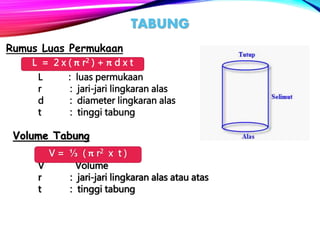
Dokumen ini menjelaskan tentang berbagai bangun ruang dalam matematika, termasuk sifat-sifat dan rumus volume serta luas permukaan kubus, balok, prisma, limas, kerucut, tabung, dan bola. Selain itu, terdapat contoh soal yang berkaitan dengan aplikasi bangun ruang dalam kehidupan sehari-hari. Dokumen ini bertujuan untuk memberikan pemahaman mendalam kepada mahasiswa tentang konsep bangun ruang dan penggunaannya.

1. Anggota kelompok 7 :
• Annisa Nurzalena
• Atikarani Noer Saleha
• Khafifa
UNIVERSITAS SRIWIJAYA
Fakultas Keguruan dan Ilmu Pendidikan Matematika
Tahun Akademik 2015/2015
BANGUN RUANG

2. Bangun
Ruang
Contoh dalam kehidupan
sehari-hari
Sifat-sifat Contoh soal
Rumus Luas
dan Volume
Kubus Balok Prisma Limas Kerucut Tabung Balok

3. BANGUN RUANG
Bangun ruang adalah bangun matematika yang
mempunyai isi ataupun volume.

4. CONTOH KUBUS DALAM KEHIDUPAN
SEHARI-HARI

5. CONTOH BALOK DALAM KEHIDUPAN
SEHARI-HARI

6. CONTOH PRISMA DALAM
KEHIDUPAN SEHARI-HARI

7. CONTOH LIMAS DALAM KEHIDUPAN
SEHARI-HARI

8. CONTOH KERUCUT DALAM
KEHIDUPAN SEHARI-HARI

9. CONTOH TABUNG DALAM KEHIDUPAN
SEHARI-HARI

10. CONTOH BOLA DALAM KEHIDUPAN
SEHARI-HARI

11. SIFAT-SIFAT KUBUS
a. Memiliki 6 sisi yang ukuran dan modelnya sama.
b. Memiliki 12 rusuk yang ukurannya sama.
c. Memiliki 8 buah sudut yang sama besar (90o).
d. Memiliki ukuran s x s x s

12. a. Memiliki 4 sisi berbentuk persegi panjang.
b. Memiliki 2 sisi yang bentuknya sama.
c. Memiliki 4 rusuk yang ukurannya sama
d. Memiliki ukuran p x l x t.
SIFAT-SIFAT BALOK

13. SIFAT-SIFAT PRISMA
Prisma segitiga :
a.mempunyai tiga buah sisi, dua buah sisi berbentuk segitiga
dan tiga buah sisi berbentuk persegi panjang.
b.mempunyai enam buah titik sudut
c.jumlah rusuknya ada sembilan
Prisma Segi-n
a. Mempunyai (n+2) sisi, (2 x n) sudut, dan (3 x n) rusuk.
b. Sisi-sisi tegak berbentuk persegi panjang atau persegi
c. Sisi alas dan sisi atas sama bentuk dan ukuran yaitu segi-n.

14. SIFAT-SIFAT LIMAS
Macam-macam limas
Nama Limas Sisi Rusuk Titik sudut Jumlah sisi
yang
berbentuk
segitiga
Limas segi tiga 4
6 4 3
Limas segi
empat
5
8 5 4
Limas segi lima 6
10 6 5
Limas segi
enam
7
12 1 6
Limas segi-n :
a. Mempunyai (n+1) sisi, (n+1) sudut, dan (2x n) rusuk.
b. Sisi-sisi tegak berbentuk segitiga.

15. a. Memiliki sisi alas yang berbentuk lingkaran.
b. Memiliki titik puncak atas.
c. Memiliki sisi (selimut) yang bentuknya lengkung.
SIFAT-SIFAT KERUCUT

16. a. Memiliki sisi alas yang berbentuk lingkaran.
b. Memiliki sisi atas yang berbentuk lingkaran.
c. Memiliki sisi (selimut) yang bentuknya lengkung.
SIFAT-SIFAT TABUNG

17. a. hanya memiliki satu buah sisi
b. tidak mempunyai titik sudut
c. hanya mempunyai sebuah sisi lengkung yang tertutup
SIFAT-SIFAT BOLA

18. KUBUS
Sebuah kubus dengan panjang rusuk 15 cm dicat pada seluruh
permukaannya. Kubus ini selanjutnya dipotong-potong menjadi
kubus kecil dengan panjang rusuk 5 cm.
a. Ada berapa kubus kecil yang terbentuk?
b. Berapa kubus kecil yang seluruh permukaannya tidak terkena cat?
c. Berapa kubus kecil yang kena cat hanya pada satu sisinya?
d. Berapa kubus kecil yang kena cat hanya pada dua sisinya?
e. Berapa kubus kecil yang kena cat hanya pada tiga sisinya?
f. Dari seluruh kubus kecil yang terbentuk, berapa total luas
permukaan yang tidak terkena cat?

19. BALOK
• Sebuah balok es berukuran 6 cm × 5 cm × 3 cm. Berapa
menit kemudian balok es itu mencair, sehingga ukurannya
menjadi 5 cm × 4 cm × 2 cm. a. Hitunglah volume balok es
setelah mencair. b. Periksalah apakah benar besar perubahan
volume balok es tersebut 50 cm3 .

20. PRISMA
Sebuah tenda berbentuk seperti gambar di bawah ini:
a.Berbentuk bangun apakah gambar di bawah.
b.Berapa meter persegi kain minimal yang dibutuhkan untuk
membuat tenda tersebut.

21. LIMAS
• Sebuah atap rumah berbentuk limas beraturan yang alasnya
berbentuk persegi dengan panjang sisi 10 cm. Jika diketahui
tinggi segitiga pada bidang tegaknya adalah 13cm, dan
tinggi limasnya adalah 12 cm. Gambarkan bentuk atap
rumah tersebut, buktikan bahwa volume atap rumah
tersebut adalah 400 cm3 !

22. KERUCUT
6. Tentukan :
a. berapa m² bahan seng yang diperlukan untuk
membuat takaran berupa kerucut tanpa tutup dengan
ukuran jari-jari r dan tingginya t masing-masing
adalah 5 cm dan 12 cm. Berapa volume air maksimal
yang dapat ditampung oleh takaran itu.
b. pertanyaan sama dengan nomor a jika kerucutnya
berukuran jari-jari dan tinggi masing-masing adalah 8
cm dan 15 cm. c. berapa takar air yang diperlukan
untuk mengisi toples berkapasitas 5 liter
menggunakan masing-masing takaran

23. TABUNG

24. BOLA
• Sebuah bola terbuat dari karet dan berjari-jari 21 cm dan
memiliki ketebalan dinding 2,1 cm. Tentukan berapa volum
karet yang diperlukan untuk membuatnya?

25. KUBUS
Rumus Luas Permukaan Kubus
L : luas permukaan
r : panjang rusuk
L = 6 x r x r
Rumus Volume
V : Volume
r : panjang rusuk
V = r x r x r

26. BALOK
Rumus Luas Permukaan
L : luas permukaan
p : panjang balok
l : lebar balok
t : tinggi balok
Volume Balok
V : volume balok
p : panjang balok
l : lebar balok
t : tinggi balok
L = 2 x [ (p x l) + (p x t) + (l x t)
V = p x l x t

27. PRISMA
L = Keliling ∆ x t x ( 2 x Luas ∆)
V = Luas Alas x t
Rumus Luas Permukaan Prisma Segitiga
L : luas permukaan
∆ : alas dan atas
segitiga
t : tinggi prisma
Volume Prisma Segitiga
V : Volume
Luas Alas : Luas ∆ = ( ½ a x t )
t : tinggi prisma

28. LIMAS
Rumus Luas Permukaan Limas
L = luas alas + luas selubung limas
Rumus Volume Limas
V : volume limas
t : tinggi limas
V = ⅓ ( luas alas x t )

29. KERUCUT
Rumus Luas Kerucut
L : luas permukaan
r : jari-jari lingkaran alas
d : diameter lingkaran alas
t : tinggi kerucut
Volume Kerucut
V : volume
r : jari-jari lingkaran alas
t : tinggi kerucut
L = π r2 + π d x t
V = ⅓ ( π r2 x t )

30. TABUNG
Rumus Luas Permukaan
L : luas permukaan
r : jari-jari lingkaran alas
d : diameter lingkaran alas
t : tinggi tabung
Volume Tabung
V Volume
r : jari-jari lingkaran alas atau atas
t : tinggi tabung
L = 2 x ( π r2 ) + π d x t
V = ⅓ ( π r2 x t )

31. BOLA
Rumus Luas Permukaan Bola
L : luas permukaan
r : jari-jari bola
Rumus Volume Bola
V : volume
r : jari-jari bola
L = 4 π r2
V = 4/3 π r3