Uploaded bytahangbuku
DOCX, PDF12,937 views

Bab 10

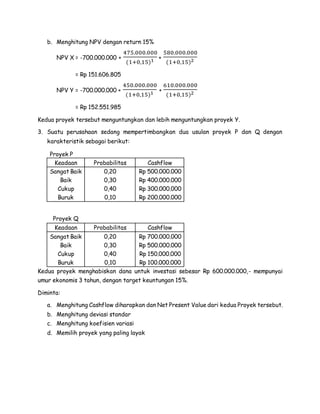
Dokumen tersebut berisi soal-soal latihan tentang analisis risiko investasi pada beberapa proyek. Terdapat tiga soal yang masing-masing meminta perhitungan nilai yang diharapkan, deviasi standar, dan NPV beberapa proyek beserta pemilihan proyek yang paling layak berdasarkan analisis tersebut.

Embed presentation

Downloaded 25 times
SOAL-SOAL LATIHAN 1. Suatu proyek investasi membutuhkan dana sebesar Rp 600.000.000,- yang mempunyai umur ekomomis 2 tahun. Cashflow yang akan diterima dengan probabilitasnya adalah sebagai berikut: Tahun 1 Tahun 2 Probabilitas Cashflow Probabilitas Cashflow 0,15 100.000.000 0,15 150.000.000 0,20 200.000.000 0,20 250.000.000 0,30 300.000.000 0,30 350.000.000 0,20 400.000.000 0,20 450.000.000 0,15 500.000.000 0,15 550.000.000 a. Hitunglah nilai yang diharapkan dan deviasi standarnya untuk tahun 1 dan tahun 2 b. Hitunglah Net Present Value dan deviasi standar NPV-nya JAWAB a. Nilai yang diharapkan  Tahun 1 100.000.000 x 0,15 = Rp 15.000.000 200.000.000 x 0,20 = Rp 40.000.000 300.000.000 x 0,30 = Rp 90.000.000 400.000.000 x 0,20 = Rp 80.000.000 500.000.000 x 0,15 = Rp 75.000.000 Nilai yang diharapkan = Rp 300.000.000  Tahun 2 150.000.000 x 0,15 = Rp 22.500.000 250.000.000 x 0,20 = Rp 50.000.000 350.000.000 x 0,30 = Rp 105.000.000 450.000.000 x 0,20 = Rp 90.000.000 550.000.000 x 0,15 = Rp 82.500.000 Nilai yang diharapkan = Rp 350.000.000 Menghitung deviasi standar  Tahun 1 (100.000.000 - 300.000.000)2 x 0,15 = Rp 6.000.000.000.000.000 (200.000.000 - 300.000.000) 2 x 0,20 = Rp 2.000.000.000.000.000 (300.000.000 - 300.000.000)2 x 0,30 = Rp 0
(400.000.000 – 300.000.000)2 x 0,20 = Rp 2.000.000.000.000.000 (500.000.000 – 300.000.000)2 x 0.15 = Rp 6.000.000.000.000.000 Rp 16.000.000.000.000.000  Investasi Tahun 1 = √16.000.000.000.000.000 = 126.491.106,4  Tahun 2 (150.000.000 - 350.000.000)2 x 0,15 = Rp 6.000.000.000.000.000 (250.000.000 – 350.000.000) 2 x 0,20 = Rp 2.000.000.000.000.000 (350.000.000 - 350.000.000)2 x 0,30 = Rp 0 (450.000.000 – 350.000.000)2 x 0,20 = Rp 2.000.000.000.000.000 (550.000.000 – 350.000.000)2 x 0.15 = Rp 6.000.000.000.000.000 Rp 16.000.000.000.000.000  Investasi Tahun 2 = √16.000.000.000.000.000 = 126.491.106,4 b. Menghitung NPV NPV = -600.000.000 + 300.000.000 (1+0,05)1 + 350.000.000 (1+0,05)2 = RP -74.480.151,23  = -74.480.151,23 = Rp 8.630,19
2. Perusahaan MELANIA akan mengevaluasi dua buah proyek X dan Y yang mempunyai umur investasi 2 tahun. Dana yang dibutuhkan untuk investasi sebesar Rp 700.000.000,- Hasil estimasi aliran kas selama 3 tahun dan probabilitasnya adalah sebagai berikut: Tahun PROYEK X PROYEK Y Probabilitas Cashflow Probabilitas Cashflow 1 0,25 300.000.000 0,30 350.000.000 0,50 500.000.000 0,40 450.000.000 0,25 600.000.000 0,30 550.000.000 2 0,20 400.000.000 0,20 550.000.000 0,60 600.000.000 0,60 600.000.000 0,20 700.000.000 0,20 650.000.000 Diminta: a. Menghitung Expected Value dari kedua proyek dan deviasi standar kedua proyek b. Menghitung NPV dengan return 15% JAWAB a. Nilai yang diharapkan  PROYEK X Tahun 1 Rp 300.000.000 x 0,25 = Rp 75.000.000 Rp 500.000.000 x 0,50 = Rp 250.000.000 Rp 600.000.000 x 0,25 = Rp 150.000.000 Nilai yang diharapkan = Rp 475.000.000 Tahun 2 Rp 400.000.000 x 0,20 = Rp 80.000.000 Rp 600.000.000 x 0,60 = Rp 360.000.000 Rp 700.000.000 x 0,20 = Rp 140.000.000 Nilai yang diharapkan = Rp 580.000.000  PROYEK Y Tahun 1 Rp 350.000.000 x 0,30 = Rp 105.000.000 Rp 450.000.000 x 0,40 = Rp 180.000.000 Rp 550.000.000 x 0,30 = Rp 165.000.000 Nilai yang diharapkan = Rp 450.000.000 Tahuni 2 Rp 550.000.000 x 0,20 = Rp 110.000.000 Rp 600.000.000 x 0,60 = Rp 360.000.000 Rp 700.000.000 x 0,20 = Rp 140.000.000 Nilai yang diharapkan = Rp 610.000.000
Menghitung Deviasi Standar  PROYEK X Tahun 1 (300.000.000 – 475.000.000)2 x 0,25 = Rp 7.656.250.000.000.000 (500.000.000 – 475.000..000)2 x 0,50 = Rp 312.500.000.000.000 (600.000.000 – 475.000.000)2 x 0,25 = Rp 3.906.250.000.000.000 = Rp 11.875.000.000.000.000  =  11.875.000.000.000.000 = 108.972.473,6 Tahun 2 (400.000.000 – 580.000.000)2 x 0,25 = Rp 8.100.000.000.000.000 (600.000.000 – 580.000.000)2 x 0,60 = Rp 176.258.400.000.000.000 (700.000.000 – 580.000.000)2 x 0,20 = Rp 2.880.000.000.000.000 = Rp 187.238.400.000.000.000  =  187.238.400.000.000.000 = 432.710.526,8  PROYEK Y Tahun 1 (350.000.000 – 450.000.000)2 x 0,30 = Rp 3.000.000.000.000.000 (450.000.000 – 450.000.000)2 x 0,40 = Rp 0 (550.000.000 – 450.000.000)2 x 0,30 = Rp 3.000.000.000.000.000 = Rp 6.000.000.000.000.000  =  6.000.000.000.000.000 = 77.459.666,92 Tahun 2 (550.000.000 – 610.000.000)2 x 0,20 = Rp 720.000.000.000.000 (600.000.000 – 610.000.000)2 x 0,60 = Rp 60.000.000.000.000 (650.000.000 – 610.000.000)2 x 0,20 = Rp 320.000.000.000.000 = Rp 1.100.000.000.000.000  =  1.100.000.000.000.000 = 33.166.247,9
b. Menghitung NPV dengan return 15% NPV X = -700.000.000 + 475.000.000 (1+0,15)1 + 580.000.000 (1+0,15)2 = Rp 151.606.805 NPV Y = -700.000.000 + 450.000.000 (1+0,15)1 + 610.000.000 (1+0,15)2 = Rp 152.551.985 Kedua proyek tersebut menguntungkan dan lebih menguntungkan proyek Y. 3. Suatu perusahaan sedang mempertimbangkan dua usulan proyek P dan Q dengan karakteristik sebagai berikut: Proyek P Keadaan Probabilitas Cashflow Sangat Baik 0,20 Rp 500.000.000 Baik 0,30 Rp 400.000.000 Cukup 0,40 Rp 300.000.000 Buruk 0,10 Rp 200.000.000 Proyek Q Keadaan Probabilitas Cashflow Sangat Baik 0,20 Rp 700.000.000 Baik 0,30 Rp 500.000.000 Cukup 0,40 Rp 150.000.000 Buruk 0,10 Rp 100.000.000 Kedua proyek menghabiskan dana untuk investasi sebesar Rp 600.000.000,- mempunyai umur ekonomis 3 tahun, dengan target keuntungan 15%. Diminta: a. Menghitung Cashflow diharapkan dan Net Present Value dari kedua Proyek tersebut. b. Menghitung deviasi standar c. Menghitung koefisien variasi d. Memilih proyek yang paling layak
JAWAB: a. Menghitung besarnya Cashflow diharapkan Proyek P Rp 500.000.000 x 0,20 = Rp 100.000.000 Rp 400.000.000 x 0,30 = Rp 120.000.000 Rp 300.000.000 x 0,40 = Rp 120.000.000 Rp 200.000.000 x 0,10 = Rp 20.000.000 Cashflow diharapkan Rp 360.000.000 Proyek Q Rp 700.000.000 x 0,20 = Rp 140.000.000 Rp 500.000.000 x 0,30 = Rp 150.000.000 Rp 150.000.000 x 0,40 = Rp 60.000.000 Rp 100.000.000 x 0,10 = Rp 10.000.000 Cashflow diharapkan Rp 360.000.000 Menghitung NPV Proyek P = 360.000.000 (1+0,15)1 = 360.000.000 1,15 = Rp 313.043.478,3 = 360.000.000 (1+0,15)2 = 360.000.000 1,3225 = Rp 272.211.720,2 = 360.000.000 (1+0,15)3 = 360.000.000 1 ,520875 = Rp 236.705.843,7 = Rp 821.961.042,2 Investasi = Rp 600.000.000 NPV = Rp 221.961.042,2 Karena proyek P dan Q menghasilkan cashflow yang diharapkan sama, maka NPV-nya juga sama.
b. Menghitung deviasi standar Proyek P Tahun V E(V) {V – E(V)}2 P {V – E(V)}2 x P 1 500.000.000 360.000.000 19.600.000.000.000.000 0,20 3.920.000.000.000.000 2 400.000.000 360.000.000 1.600.000.000.000.000 0,30 480.000.000.000.000 3 300.000.000 360.000.000 3.600.000.000.000.000 0,40 1.440.000.000.000.000 4 200.000.000 360.000.000 25.600.000.000.000.000 0,10 2.560.000.000.000.000 8.400.000.000.000.000 P = 8.400.000.000.000.000 = Rp 91.651.513,9 Proyek Q Tahun V EV V - E 2 P v-EVxP 1 700.000.000 360.000.000 115.600.000.000.000.000 0,20 23.120.000.000.000.000 2 500.000.000 360.000.000 19.600.000.000.000.000 0,30 5.880.000.000.000.000 3 150.000.000 360.000.000 44.100.000.000.000.000 0,40 17.640.000.000.000.000 4 100.000.000 360.000.000 67.600.000.000.000.000 0,10 6.760.000.000.000.000 53.400.000.000.000.000 Q = 53.400.000.000.000.000 = Rp 231.084.400,2 c. Koefisien variasi Proyek P = 91.651.513,9 360.000.000 = 0,25 Proyek Q = 231.084.400,2 360.000.000 = 0,64 Kesimpulannya : Proyek Q mempunyai resiko yang lebih tinggi dibanding Proyek P. d. Berdasarkan analisis NPV, kedua proyek mengalami NPV yang sama namun proyek P mempunyai resiko yang lebih rendah sehingga proyek P lebih layak.

More Related Content

PPTX
ARUS KAS DAN BEBERAPA TOPIK LAIN DALAM PENGANGGARAN MODAL
byRoni Saputra
 
DOCX
Risk Analysis and Project Evaluation/Abshor.Marantika/Alviyanti Nawangsari/3-03
byAlviyantiNawangsari
 
DOC
CAPITAL BUDGETING-AIBK-SESI 4
byYoyo Sudaryo
 
PPT
7. Capital Budgeting.ppt
byNellyAgustini
 
PPSX
Capital Budgeting
bySyafril Djaelani,SE, MM
 
DOC
Keputusan investasi
bytonyherman87
 
PPTX
Bab. 13 Keputusan Investasi Modal
byFitri Ayu Kusuma Wijayanti
 
PPTX
Pertemuan 4 the time value of money
byCenter For Economic Policy Institute (CEPAT)
 
ARUS KAS DAN BEBERAPA TOPIK LAIN DALAM PENGANGGARAN MODAL
byRoni Saputra
 
Risk Analysis and Project Evaluation/Abshor.Marantika/Alviyanti Nawangsari/3-03
byAlviyantiNawangsari
 
CAPITAL BUDGETING-AIBK-SESI 4
byYoyo Sudaryo
 
7. Capital Budgeting.ppt
byNellyAgustini
 
Capital Budgeting
bySyafril Djaelani,SE, MM
 
Keputusan investasi
bytonyherman87
 
Bab. 13 Keputusan Investasi Modal
byFitri Ayu Kusuma Wijayanti
 
Pertemuan 4 the time value of money
byCenter For Economic Policy Institute (CEPAT)
 

What's hot

DOCX
Contoh Soal Pengantar Ekonomi https://www.masterfair.xyz/
byFair Nurfachrizi
 
PDF
Akuntansi biaya _ semester III
byhasril ariel
 
PPT
Bab 4 bunga majemuk
byMirabela Islami
 
PPTX
elastisitas silang dan elastisitas pendapatan
byEkinanda Anggita
 
PPTX
AKUTANSI PERSEROAN TERBATAS
byPuja Lestari
 
PPTX
Time value of money
byPT Lion Air
 
PPTX
Manajemen keuangan part 2 of 5
byJudianto Nugroho
 
PPTX
Suku Bunga, Penilaian Obligasi, dan Penilaian Saham
byNinnasi Muttaqiin
 
PDF
Latihan + jawaban mikro 1 (uts) - FEUI
byFarah Fauziah Hilman
 
PPTX
Teori Perilaku Konsumen
byvadilla mutia
 
PPTX
Tugas manajemen keuangan 2 - Manajemen Piutang & Persediaan - 2019
byLulu Wildatiumi
 
PPSX
Time Value Of Money
byRoesdaniel Ibrahim, ST. CHt.
 
PDF
Anggaranperusahaan 101214094831-phpapp01
byarwianthy
 
PPT
Bab 8 multiplier
byYusron Blacklist
 
PPT
Analisis biaya-relevan-edit
byRico Andreas Sagala
 
PPTX
Biaya modal dan Struktur Modal MNC (Multi National Corporate)
byNurmansyah Arif W
 
DOCX
Matematika ekonomi (Keuntungan Maksimum)
byKristalina Dewi
 
PDF
[Modul] matematika ekonomi
byheru putra
 
PPT
Ppt akuntansi differensial
byYoshita Elsyanti
 
PPT
linear programming metode simplex
byBambang Kristiono
 
Contoh Soal Pengantar Ekonomi https://www.masterfair.xyz/
byFair Nurfachrizi
 
Akuntansi biaya _ semester III
byhasril ariel
 
Bab 4 bunga majemuk
byMirabela Islami
 
elastisitas silang dan elastisitas pendapatan
byEkinanda Anggita
 
AKUTANSI PERSEROAN TERBATAS
byPuja Lestari
 
Time value of money
byPT Lion Air
 
Manajemen keuangan part 2 of 5
byJudianto Nugroho
 
Suku Bunga, Penilaian Obligasi, dan Penilaian Saham
byNinnasi Muttaqiin
 
Latihan + jawaban mikro 1 (uts) - FEUI
byFarah Fauziah Hilman
 
Teori Perilaku Konsumen
byvadilla mutia
 
Tugas manajemen keuangan 2 - Manajemen Piutang & Persediaan - 2019
byLulu Wildatiumi
 
Time Value Of Money
byRoesdaniel Ibrahim, ST. CHt.
 
Anggaranperusahaan 101214094831-phpapp01
byarwianthy
 
Bab 8 multiplier
byYusron Blacklist
 
Analisis biaya-relevan-edit
byRico Andreas Sagala
 
Biaya modal dan Struktur Modal MNC (Multi National Corporate)
byNurmansyah Arif W
 
Matematika ekonomi (Keuntungan Maksimum)
byKristalina Dewi
 
[Modul] matematika ekonomi
byheru putra
 
Ppt akuntansi differensial
byYoshita Elsyanti
 
linear programming metode simplex
byBambang Kristiono
 

Bab 10

  • 1.
    SOAL-SOAL LATIHAN 1.Suatu proyek investasi membutuhkan dana sebesar Rp 600.000.000,- yang mempunyai umur ekomomis 2 tahun. Cashflow yang akan diterima dengan probabilitasnya adalah sebagai berikut: Tahun 1 Tahun 2 Probabilitas Cashflow Probabilitas Cashflow 0,15 100.000.000 0,15 150.000.000 0,20 200.000.000 0,20 250.000.000 0,30 300.000.000 0,30 350.000.000 0,20 400.000.000 0,20 450.000.000 0,15 500.000.000 0,15 550.000.000 a. Hitunglah nilai yang diharapkan dan deviasi standarnya untuk tahun 1 dan tahun 2 b. Hitunglah Net Present Value dan deviasi standar NPV-nya JAWAB a. Nilai yang diharapkan  Tahun 1 100.000.000 x 0,15 = Rp 15.000.000 200.000.000 x 0,20 = Rp 40.000.000 300.000.000 x 0,30 = Rp 90.000.000 400.000.000 x 0,20 = Rp 80.000.000 500.000.000 x 0,15 = Rp 75.000.000 Nilai yang diharapkan = Rp 300.000.000  Tahun 2 150.000.000 x 0,15 = Rp 22.500.000 250.000.000 x 0,20 = Rp 50.000.000 350.000.000 x 0,30 = Rp 105.000.000 450.000.000 x 0,20 = Rp 90.000.000 550.000.000 x 0,15 = Rp 82.500.000 Nilai yang diharapkan = Rp 350.000.000 Menghitung deviasi standar  Tahun 1 (100.000.000 - 300.000.000)2 x 0,15 = Rp 6.000.000.000.000.000 (200.000.000 - 300.000.000) 2 x 0,20 = Rp 2.000.000.000.000.000 (300.000.000 - 300.000.000)2 x 0,30 = Rp 0
  • 2.
    (400.000.000 – 300.000.000)2x 0,20 = Rp 2.000.000.000.000.000 (500.000.000 – 300.000.000)2 x 0.15 = Rp 6.000.000.000.000.000 Rp 16.000.000.000.000.000  Investasi Tahun 1 = √16.000.000.000.000.000 = 126.491.106,4  Tahun 2 (150.000.000 - 350.000.000)2 x 0,15 = Rp 6.000.000.000.000.000 (250.000.000 – 350.000.000) 2 x 0,20 = Rp 2.000.000.000.000.000 (350.000.000 - 350.000.000)2 x 0,30 = Rp 0 (450.000.000 – 350.000.000)2 x 0,20 = Rp 2.000.000.000.000.000 (550.000.000 – 350.000.000)2 x 0.15 = Rp 6.000.000.000.000.000 Rp 16.000.000.000.000.000  Investasi Tahun 2 = √16.000.000.000.000.000 = 126.491.106,4 b. Menghitung NPV NPV = -600.000.000 + 300.000.000 (1+0,05)1 + 350.000.000 (1+0,05)2 = RP -74.480.151,23  = -74.480.151,23 = Rp 8.630,19
  • 3.
    2. Perusahaan MELANIAakan mengevaluasi dua buah proyek X dan Y yang mempunyai umur investasi 2 tahun. Dana yang dibutuhkan untuk investasi sebesar Rp 700.000.000,- Hasil estimasi aliran kas selama 3 tahun dan probabilitasnya adalah sebagai berikut: Tahun PROYEK X PROYEK Y Probabilitas Cashflow Probabilitas Cashflow 1 0,25 300.000.000 0,30 350.000.000 0,50 500.000.000 0,40 450.000.000 0,25 600.000.000 0,30 550.000.000 2 0,20 400.000.000 0,20 550.000.000 0,60 600.000.000 0,60 600.000.000 0,20 700.000.000 0,20 650.000.000 Diminta: a. Menghitung Expected Value dari kedua proyek dan deviasi standar kedua proyek b. Menghitung NPV dengan return 15% JAWAB a. Nilai yang diharapkan  PROYEK X Tahun 1 Rp 300.000.000 x 0,25 = Rp 75.000.000 Rp 500.000.000 x 0,50 = Rp 250.000.000 Rp 600.000.000 x 0,25 = Rp 150.000.000 Nilai yang diharapkan = Rp 475.000.000 Tahun 2 Rp 400.000.000 x 0,20 = Rp 80.000.000 Rp 600.000.000 x 0,60 = Rp 360.000.000 Rp 700.000.000 x 0,20 = Rp 140.000.000 Nilai yang diharapkan = Rp 580.000.000  PROYEK Y Tahun 1 Rp 350.000.000 x 0,30 = Rp 105.000.000 Rp 450.000.000 x 0,40 = Rp 180.000.000 Rp 550.000.000 x 0,30 = Rp 165.000.000 Nilai yang diharapkan = Rp 450.000.000 Tahuni 2 Rp 550.000.000 x 0,20 = Rp 110.000.000 Rp 600.000.000 x 0,60 = Rp 360.000.000 Rp 700.000.000 x 0,20 = Rp 140.000.000 Nilai yang diharapkan = Rp 610.000.000
  • 4.
    Menghitung Deviasi Standar  PROYEK X Tahun 1 (300.000.000 – 475.000.000)2 x 0,25 = Rp 7.656.250.000.000.000 (500.000.000 – 475.000..000)2 x 0,50 = Rp 312.500.000.000.000 (600.000.000 – 475.000.000)2 x 0,25 = Rp 3.906.250.000.000.000 = Rp 11.875.000.000.000.000  =  11.875.000.000.000.000 = 108.972.473,6 Tahun 2 (400.000.000 – 580.000.000)2 x 0,25 = Rp 8.100.000.000.000.000 (600.000.000 – 580.000.000)2 x 0,60 = Rp 176.258.400.000.000.000 (700.000.000 – 580.000.000)2 x 0,20 = Rp 2.880.000.000.000.000 = Rp 187.238.400.000.000.000  =  187.238.400.000.000.000 = 432.710.526,8  PROYEK Y Tahun 1 (350.000.000 – 450.000.000)2 x 0,30 = Rp 3.000.000.000.000.000 (450.000.000 – 450.000.000)2 x 0,40 = Rp 0 (550.000.000 – 450.000.000)2 x 0,30 = Rp 3.000.000.000.000.000 = Rp 6.000.000.000.000.000  =  6.000.000.000.000.000 = 77.459.666,92 Tahun 2 (550.000.000 – 610.000.000)2 x 0,20 = Rp 720.000.000.000.000 (600.000.000 – 610.000.000)2 x 0,60 = Rp 60.000.000.000.000 (650.000.000 – 610.000.000)2 x 0,20 = Rp 320.000.000.000.000 = Rp 1.100.000.000.000.000  =  1.100.000.000.000.000 = 33.166.247,9
  • 5.
    b. Menghitung NPVdengan return 15% NPV X = -700.000.000 + 475.000.000 (1+0,15)1 + 580.000.000 (1+0,15)2 = Rp 151.606.805 NPV Y = -700.000.000 + 450.000.000 (1+0,15)1 + 610.000.000 (1+0,15)2 = Rp 152.551.985 Kedua proyek tersebut menguntungkan dan lebih menguntungkan proyek Y. 3. Suatu perusahaan sedang mempertimbangkan dua usulan proyek P dan Q dengan karakteristik sebagai berikut: Proyek P Keadaan Probabilitas Cashflow Sangat Baik 0,20 Rp 500.000.000 Baik 0,30 Rp 400.000.000 Cukup 0,40 Rp 300.000.000 Buruk 0,10 Rp 200.000.000 Proyek Q Keadaan Probabilitas Cashflow Sangat Baik 0,20 Rp 700.000.000 Baik 0,30 Rp 500.000.000 Cukup 0,40 Rp 150.000.000 Buruk 0,10 Rp 100.000.000 Kedua proyek menghabiskan dana untuk investasi sebesar Rp 600.000.000,- mempunyai umur ekonomis 3 tahun, dengan target keuntungan 15%. Diminta: a. Menghitung Cashflow diharapkan dan Net Present Value dari kedua Proyek tersebut. b. Menghitung deviasi standar c. Menghitung koefisien variasi d. Memilih proyek yang paling layak
  • 6.
    JAWAB: a. Menghitungbesarnya Cashflow diharapkan Proyek P Rp 500.000.000 x 0,20 = Rp 100.000.000 Rp 400.000.000 x 0,30 = Rp 120.000.000 Rp 300.000.000 x 0,40 = Rp 120.000.000 Rp 200.000.000 x 0,10 = Rp 20.000.000 Cashflow diharapkan Rp 360.000.000 Proyek Q Rp 700.000.000 x 0,20 = Rp 140.000.000 Rp 500.000.000 x 0,30 = Rp 150.000.000 Rp 150.000.000 x 0,40 = Rp 60.000.000 Rp 100.000.000 x 0,10 = Rp 10.000.000 Cashflow diharapkan Rp 360.000.000 Menghitung NPV Proyek P = 360.000.000 (1+0,15)1 = 360.000.000 1,15 = Rp 313.043.478,3 = 360.000.000 (1+0,15)2 = 360.000.000 1,3225 = Rp 272.211.720,2 = 360.000.000 (1+0,15)3 = 360.000.000 1 ,520875 = Rp 236.705.843,7 = Rp 821.961.042,2 Investasi = Rp 600.000.000 NPV = Rp 221.961.042,2 Karena proyek P dan Q menghasilkan cashflow yang diharapkan sama, maka NPV-nya juga sama.
  • 7.
    b. Menghitung deviasistandar Proyek P Tahun V E(V) {V – E(V)}2 P {V – E(V)}2 x P 1 500.000.000 360.000.000 19.600.000.000.000.000 0,20 3.920.000.000.000.000 2 400.000.000 360.000.000 1.600.000.000.000.000 0,30 480.000.000.000.000 3 300.000.000 360.000.000 3.600.000.000.000.000 0,40 1.440.000.000.000.000 4 200.000.000 360.000.000 25.600.000.000.000.000 0,10 2.560.000.000.000.000 8.400.000.000.000.000 P = 8.400.000.000.000.000 = Rp 91.651.513,9 Proyek Q Tahun V EV V - E 2 P v-EVxP 1 700.000.000 360.000.000 115.600.000.000.000.000 0,20 23.120.000.000.000.000 2 500.000.000 360.000.000 19.600.000.000.000.000 0,30 5.880.000.000.000.000 3 150.000.000 360.000.000 44.100.000.000.000.000 0,40 17.640.000.000.000.000 4 100.000.000 360.000.000 67.600.000.000.000.000 0,10 6.760.000.000.000.000 53.400.000.000.000.000 Q = 53.400.000.000.000.000 = Rp 231.084.400,2 c. Koefisien variasi Proyek P = 91.651.513,9 360.000.000 = 0,25 Proyek Q = 231.084.400,2 360.000.000 = 0,64 Kesimpulannya : Proyek Q mempunyai resiko yang lebih tinggi dibanding Proyek P. d. Berdasarkan analisis NPV, kedua proyek mengalami NPV yang sama namun proyek P mempunyai resiko yang lebih rendah sehingga proyek P lebih layak.