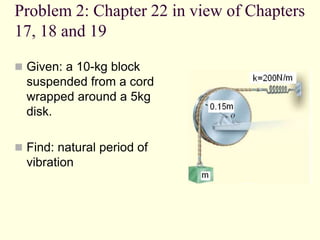
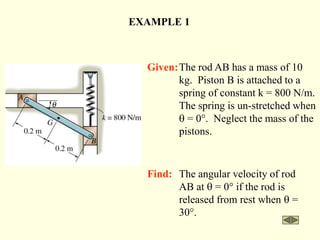
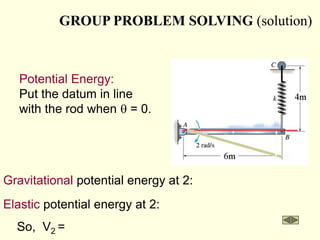
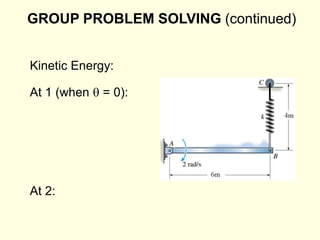
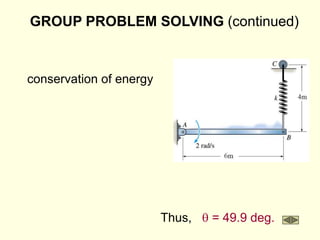
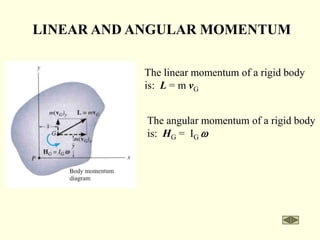
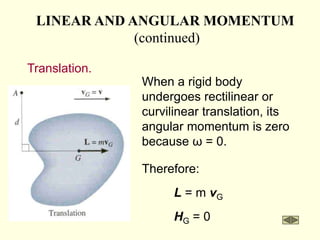
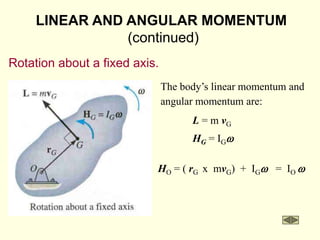
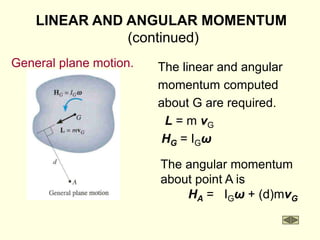
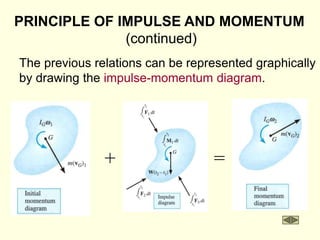
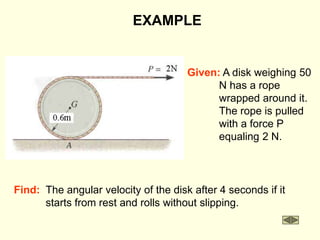
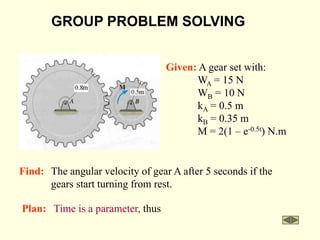
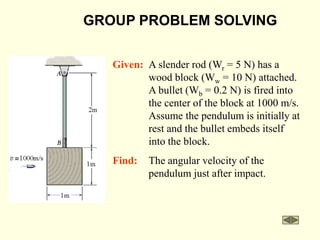
The document covers the principles of work, energy, and momentum related to rigid bodies in motion, detailing kinetic energy calculations, the work done by forces, and the conservation of energy. It explains the applications of these principles through various examples and equations, focusing on rotational and translational dynamics. Additionally, it introduces impulse and momentum analysis, providing insight into how these concepts apply to real-world scenarios like pendulums and gear systems.

1. CHAPTER 18
PLANAR KINETICS OF A RIGID BODY:
WORK AND ENERGY (Sections 18.1-18.4)
Objectives:
a) Define the various ways a
force and couple do work.
b) Apply the principle of work
and energy to a rigid body.

2. APPLICATIONS
The work of the torque
developed by the driving gears
on the two motors on the mixer
is transformed into the rotational
kinetic energy of the mixing
drum.
The work done by the compactor's
engine is transformed into the
translational kinetic energy of the
frame and the translational and
rotational kinetic energy of
its roller and wheels

3. KINETIC ENERGY
The kinetic energy of a rigid body in general
plane motion is given by
T = 1/2 m (vG)2 + 1/2 IG ω2
Several simplifications can occur.
1. Pure Translation: the
rotational kinetic energy is zero
(ω = 0):
T = 0.5 m (vG)2

4. KINETIC ENERGY (continued)
If the rotation occurs about the mass center (pure rotation), G,
then vG=0
2. Rotation: When a rigid body is rotating
about a fixed axis passing through point O,
the body has both translational and
rotational kinetic energy:
T = 0.5m(vG)2 + 0.5IGw2
Since
vG = rGw, T = 0.5(IG + m(rG)2)w2 = 0.5IOw2
T = 0.5 IG w2

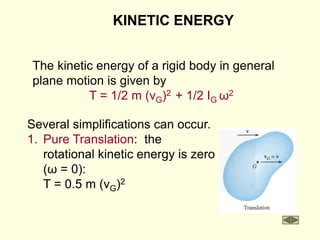
5. WORK OF A FORCE
The work done by a force is
UF =  F•dr =  (F cos θ) ds
Constant force : UFc = (Fc cos θ)s
s
Work of a weight: Uw = -WΔy.
Work of a spring force:
Us = -0.5k[(s2)2 – (s1)2]

6. FORCES THAT DO NO WORK
1. Reactions at fixed supports because the
displacement at their point of application is zero.
3. Internal forces because they always act in
equal and opposite pairs.
2. Normal and frictional forces acting
on bodies as they roll without slipping
over a rough surface since there is
no instantaneous displacement of the
point in contact with ground.

7. THE WORK OF A COUPLE
A body subjected to a couple
produces work only when it
undergoes rotation.
constant M: UM = M (q2 – q1)
If the body rotates through an angular
displacement dq, the work of the couple
moment, M, is

=
q2
q1
M dq
UM

8. PRINCIPLE OF WORK AND ENERGY
The principle states: SU1-2 = T12
i.e. the work done by all external forces and couple
moments equals the change in body’s kinetic energy
(translational and rotational).
This equation is a scalar equation. It can be applied to a
system of rigid bodies by summing contributions from all
bodies.

9. Find: Angular velocity of the disk when point G moves 0.5 m.
The disk starts from rest and rolls without slipping. The
spring is initially unstretched.
EXAMPLE
Given:The disk weighs 40 N,
has a radius of gyration
(kG) 0.6 m. A 15 N.m
moment is applied. The
spring constant is 10N/m.

10. EXAMPLE (solution)
Free body diagram of the disk:
Only the spring force and
couple moment M do work.
Spring will stretch twice the
amount of displacement of
G, or 1 m. Why?

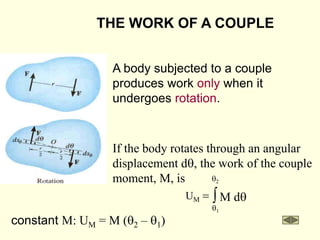
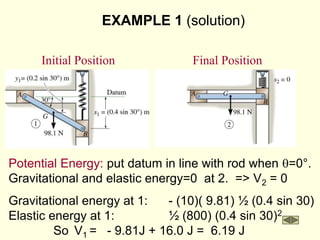
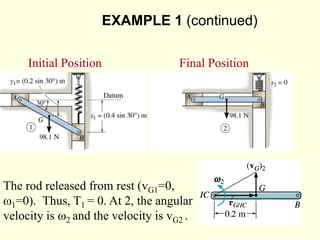
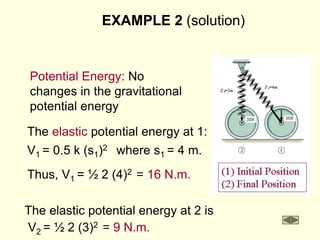
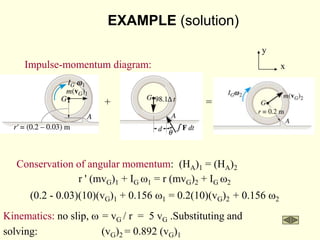
11. EXAMPLE (continued)
Work: U1-2 = -0.5k[(s2)2 – (s1)2] + M(q2 – q1)
U1-2 = -0.5(10)(12 – 0) + 15(0.5/0.8) = 4.4N.m
Kinematic relation: vG = r w = 0.8w
Kinetic energy: T1 = 0
T2 = 0.5m (vG)2 + 0.5 IG w2
T2 = 0.5(40/9.8)(0.8w)2 + 0.5(40/9.8)(0.6)2w2
T2 = 2.0 w2
Work and energy: U1-2 = T12
4.4 = 2.0 w2
w = 1.5 rad/s

12. GROUP PROBLEM SOLVING
Find: The angular velocity of the sphere when q = 45°
if the sphere rolls without slipping.
Given: A sphere weighing 10N
rolls along a semicircular
hoop. Its w equals 0
when q = 0.

13. GROUP PROBLEM SOLVING (continued)
Now calculate the _______________ :
Solution: Draw a FBD
and calculate the vertical
distance the mass center
moves.

14. GROUP PROBLEM SOLVING (continued)
A kinematic equation for finding the velocity of
the mass center is needed. It is
_________ energy:
Now apply the principle of work and energy equation:
w = 13.1 rad/s

16. PLANAR KINETICS OF A RIGID BODY:
CONSERVATION OF ENERGY (Section 18.5)
Objectives:
a) Determine the potential
energy of conservative
forces.
b) Apply the principle of
conservation of energy.

17. APPLICATIONS
Torsional spring at the
top of the door winds
up as the door is
lowered. When the door
is raised, the spring
potential energy is
transferred into
gravitational potential
energy of the door’s
weight, thus making it
easy to open.

18. CONSERVATION OF ENERGY
The conservation of energy theorem is a “simpler”
energy method for solving problems. Once again,
the problem parameter of distance is a key
indicator of when conservation of energy is a good
method for solving the problem.
If it is appropriate, conservation of energy is easier
to use than the principle of work and energy.

19. CONSERVATIVE FORCES
A force F is conservative if the work done by the
force is independent of the path.
Typical conservative forces encountered in
dynamics are gravitational forces (i.e., weight)
and elastic forces (i.e., springs).
What is a common force that is not conservative?

20. CONSERVATION OF ENERGY
When a rigid body is acted upon by a system of
conservative forces, the work done by these forces
is conserved. Thus, the sum of kinetic energy and
potential energy remains constant:
T1 + V1 = T2 + V2 = Constant
i.e. as a rigid body moves from one position to another
when acted upon by only conservative forces, kinetic
energy is converted to potential energy and vice versa.

21. GRAVITATIONAL POTENTIAL ENERGY
The gravitational potential energy is a function of the
height of the body’s center above or below a datum.
Gravitational potential energy is +ve when yG is +ve,
since the weight has the ability to do +ve work
when the body is moved back to the datum.
The gravitational potential
energy is found by:
Vg = W yG

22. ELASTIC POTENTIAL ENERGY
Spring forces are also conservative forces.
Notice that the elastic potential energy is always +ve
The potential energy of
a spring force (F = ks) is
found by the equation
Ve = ½ ks2

23. Find: The angular velocity of rod
AB at q = 0° if the rod is
released from rest when q =
30°.
EXAMPLE 1
Given:The rod AB has a mass of 10
kg. Piston B is attached to a
spring of constant k = 800 N/m.
The spring is un-stretched when
q = 0°. Neglect the mass of the
pistons.

24. EXAMPLE 1 (solution)
Potential Energy: put datum in line with rod when q=0°.
Gravitational and elastic energy=0 at 2. => V2 = 0
Gravitational energy at 1: - (10)( 9.81) ½ (0.4 sin 30)
Elastic energy at 1: ½ (800) (0.4 sin 30)2
So V1 = - 9.81J + 16.0 J = 6.19 J
Initial Position Final Position

25. EXAMPLE 1 (continued)
The rod released from rest (vG1=0,
w1=0). Thus, T1 = 0. At 2, the angular
velocity is w2 and the velocity is vG2 .
Kinetic Energy:
Initial Position Final Position

26. EXAMPLE 1 (continued)
Thus,
T2 = ½ (10)(vG2)2 + ½ (1/12)(10)(0.42)(w2)2
At 2, vA=0. Hence, vG2 = r w = 0.2 w2 .
Then, T2 = 0.2 w2
2 + 0.067 w2
2 = 0.267 w2
2
conservation of energy:
T1 + V1 = T2 + V2
0 + 6.19 = 0.267w2
2 + 0 => w2 = 4.82 rad/s

27. EXAMPLE 2
Given: The weight of the disk is 30 N
and its kG equals 0.6 m. The
spring has a stiffness of 2 N/m
and an unstretched length of 1m.
Find: The angular velocity at the
instant G moves 3 m to the
left. The disk is released
from rest in the position
shown and rolls without
slipping.

28. EXAMPLE 2 (solution)
Potential Energy: No
changes in the gravitational
potential energy
The elastic potential energy at 1:
V1 = 0.5 k (s1)2 where s1 = 4 m.
Thus, V1 = ½ 2 (4)2 = 16 N.m.
The elastic potential energy at 2 is
V2 = ½ 2 (3)2 = 9 N.m.

29. EXAMPLE 2 (continued)
Kinetic Energy:
Released from rest: vG1=w1=0, T1=0
At 2, w2 and vG2:
T2 = ½ m (vG2)2 + ½ IG (w2) 2
= ½ (30/9.8) (vG2)2 + ½ (30/9.8) 0.62 (w2) 2
Disk is rolling without slipping: vG2 = (0.75 w2)
T2 = ½(30/9.8)(0.75 w2)2 + ½(30/9.8) 0.62 (w2)2 = 1.41 (w2)2

30. EXAMPLE 2 (continued)
conservation of energy:
T1 + V1 = T2 + V2
0 +16.0 = 1.41 w2
2 + 9
Solving , w2 = 2.23 rad/s

31. GROUP PROBLEM SOLVING
Find: The angle (measured down from the horizontal)
to which the bar rotates before it stops its initial
downward movement.
Given:A 50 N bar is rotating
downward at 2 rad/s.
The spring has an
unstretched length of
2m and a spring
constant of 12 N/m

32. GROUP PROBLEM SOLVING (solution)
Potential Energy:
Put the datum in line
with the rod when q = 0.
Gravitational potential energy at 2:
Elastic potential energy at 2:
So, V2 =

33. GROUP PROBLEM SOLVING (continued)
At 1 (when q = 0):
Kinetic Energy:
At 2:

34. GROUP PROBLEM SOLVING (continued)
conservation of energy
Thus, q = 49.9 deg.

36. CHAPTER 19
PLANAR KINETICS: IMPULSE AND
MOMENTUM (Sections 19.1-19.2)
Today’s Objectives:
a) Develop formulations for
the linear and angular
momentum of a body.
b) Apply the principle of
linear and angular
impulse and momentum.

37. APPLICATIONS
As the pendulum swings downward,
its angular momentum and linear
momentum both increase. By
calculating its momenta in the vertical
position, we can calculate the impulse
the pendulum exerts when it hits the
test specimen.
The space shuttle has several engines
that exert thrust on the shuttle when
they are fired. By firing different
engines, the pilot can control the
motion and direction of
the shuttle.

38. LINEAR AND ANGULAR MOMENTUM
The linear momentum of a rigid body
is: L = m vG
The angular momentum of a rigid body
is: HG = IG w

39. LINEAR AND ANGULAR MOMENTUM
(continued)
Translation.
When a rigid body
undergoes rectilinear or
curvilinear translation, its
angular momentum is zero
because ω = 0.
Therefore:
L = m vG
HG = 0

40. Rotation about a fixed axis.
HO = ( rG x mvG) + IGw = IO w
The body’s linear momentum and
angular momentum are:
L = m vG
HG = IGw
LINEAR AND ANGULAR MOMENTUM
(continued)

41. General plane motion. The linear and angular
momentum computed
about G are required.
L = m vG
HG = IGω
The angular momentum
about point A is
HA = IGω + (d)mvG
LINEAR AND ANGULAR MOMENTUM
(continued)

42. PRINCIPLE OF IMPULSE AND MOMENTUM
The principle is developed by combining the equation of motion
with kinematics. The resulting equations allow a direct solution
to problems involving force, velocity, and time.
Linear impulse-linear momentum equation:
L1 + F dt = L2 or (mvG)1 + F dt = (mvG)2
t2
t1
 
t2
t1
 
Angular impulse-angular momentum equation:
(HG)1 + MG dt = (HG)2 or IGw1 + MG dt = IGw2
t2
t1
 
t2
t1
 

43. PRINCIPLE OF IMPULSE AND MOMENTUM
(continued)
The previous relations can be represented graphically
by drawing the impulse-momentum diagram.
+ =

44. Find: The angular velocity of the disk after 4 seconds if it
starts from rest and rolls without slipping.
EXAMPLE
Given: A disk weighing 50
N has a rope
wrapped around it.
The rope is pulled
with a force P
equaling 2 N.

45. EXAMPLE (solution)
Impulse-momentum diagram:
Kinematics: (vG)2 = r w2
t2
t1

Impulse & Momentum: (HA)1 + MA dt = (HA)2
(P t) 2 r = (mvG)2 r + IGw2 = m r2 w2 + 0.5 m r2 w2 = 1.5 m r2 w2
3.5 rad/s
3(50/9.81)(0.6)
4(2)(4)
3mr
4 Pt
w2
=
=
=
(m vG)1 (m vG)2
G G
IGw1 IG w2
P t
F t
N t
W t
r
+ =
A
y
x

46. GROUP PROBLEM SOLVING
Find: The angular velocity of gear A after 5 seconds if the
gears start turning from rest.
Plan: Time is a parameter, thus
Given: A gear set with:
WA = 15 N
WB = 10 N
kA = 0.5 m
kB = 0.35 m
M = 2(1 – e-0.5t) N.m

47. GROUP PROBLEM SOLVING (continued)
Impulse-momentum diagrams:
Gear A: y
x
Gear B:
Solution:

48. GROUP PROBLEM SOLVING (continued)
Angular impulse & momentum relation for gear A about point
A yields:
For gear B:
Kinematics:

49. GROUP PROBLEM SOLVING (continued)
and wA = 14.4 rad/s

51. CONSERVATION OF MOMENTUM
(Section 19.3)
Objectives:
a) Understand the conditions
for conservation of linear and
angular momentum
b) Use the condition of
conservation of linear/
angular momentum

52. APPLICATIONS
A skater spends a lot of time either spinning on the ice or
rotating through the air. To spin fast, or for a long time, the
skater must develop a large amount of angular momentum.
If the skater’s angular momentum is constant, can the
skater vary his rotational speed? How?
The skater spins faster when the arms are drawn in and
slower when the arms are extended. Why?

53. CONSERVATION OF LINEAR MOMENTUM
Recall that the linear impulse and momentum relationship is
L1 + F dt = L2 or (m vG)1 + F dt = (m vG)2
t2
t1
 
t2
t1
 
If the sum of all the linear impulses acting on the rigid
body (or a system of rigid bodies) is zero, all the impulse
terms are zero. Thus, the linear momentum for a rigid
body (or system) is constant, or conserved. So L1 = L2.
0
0
This equation is referred to as the conservation of linear
momentum. The conservation of linear momentum
equation can be used if the linear impulses are small or
non-impulsive.

54. CONSERVATION OFANGULAR MOMENTUM
The angular impulse-angular momentum relationship is:
(HG)1 + MG dt = (HG)2 or IGw1 + MG dt = IGw2
t2
t1
 
t2
t1
 
0
0
Similarly, if the sum of all the angular impulses due to
external forces acting on the rigid body (or a system of rigid
bodies) is zero, all the impulse terms are zero. Thus, angular
momentum is conserved . The resulting equation is referred to
as the conservation of angular momentum or (HG)1 = (HG)2 .
If the initial condition of the rigid body (or system) is known,
conservation of momentum is often used to determine the final
linear or angular velocity of a body just after an event occurs.

55. Given: A 10 kg wheel
(IG = 0.156 kg·m2) rolls
without slipping and
does not bounce at A.
Find: The minimum velocity, vG, of the wheel to just roll over
the obstruction at A.
EXAMPLE
Note: Since no slipping or bouncing occurs, the wheel pivots about
point A. The force at A is much greater than the weight, and since the
time of impact is very short, the weight can be considered non-impulsive.
The reaction force at A, since we don’t know either its direction or
magnitude, can be eliminated by applying the conservation of angular
momentum equation about A.

56. Conservation of angular momentum: (HA)1 = (HA)2
r ' (mvG)1 + IG w1 = r (mvG)2 + IG w2
(0.2 - 0.03)(10)(vG)1 + 0.156 w1 = 0.2(10)(vG)2 + 0.156 w2
Kinematics: no slip, w = vG / r = 5 vG .Substituting and
solving: (vG)2 = 0.892 (vG)1
Impulse-momentum diagram:
+ =
x
y
EXAMPLE (solution)

57. EXAMPLE (continued)
T2 + V2 = T3 + V3
{½(10)(vG)2
2 + ½(0.156)w2
2 } + 0 = 0 + 98.1 (0.03)
Substituting w2 = 5 (vG)2 and (vG)2 = 0.892 (vG)1 and
solving yields: (vG)1 = 0.729 m/s, (vG)2 = 0.65 m/s
To complete the solution,
conservation of energy can be used.
Since it cannot be used for the
impact (why?), it is applied just
after the impact. In order to roll over
the bump, the wheel must go to
position 3 from 2. When (vG)2 is a
minimum, (vG)3 is zero. Why?

58. GROUP PROBLEM SOLVING
Find: The angular velocity of the
pendulum just after impact.
Given: A slender rod (Wr = 5 N) has a
wood block (Ww = 10 N) attached.
A bullet (Wb = 0.2 N) is fired into
the center of the block at 1000 m/s.
Assume the pendulum is initially at
rest and the bullet embeds itself
into the block.

59. GROUP PROBLEM SOLVING (continued)
To use conservation of angular momentum,
IA = ?
IA = 7.2kg.m2
Solution:
First draw a FBD.

60. GROUP PROBLEM SOLVING (continued)
Solving yields:
w2 = 7.0 rad/s
Apply the conservation of angular momentum equation:

62. CHAPTER 22
VIBRATIONS (section 22.1)
Objectives:
Discuss Undamped single
degree of freedom (SDOF)
vibration of a rigid body

63. Vibration definition
 Vibration is the periodic motion of a body or
system of connected bodies displaced from a
position of equilibrium
 Types of vibrations
 Free vibrations: motion is maintained by
conservative forces (like gravitational or elastic
restoring forces).
 Forced vibrations: motion is caused by
external periodic or intermittent forces.

64. Undamped free response for SDOF systems
If you displace mass m a
distance u from equilibrium
position and release it,
vibration occurs

65. Undamped free response for SDOF systems
(cont):
 Equilibrium eq:
 A linear, constant
coefficients, homogeneous,
second order ordinary
differential equation
2
2
2
2
0
u
Ku m
t
u
m Ku
t

 =


 =

2
2
2
2
2
0
0
cos sin
n
n n
u
m ku
t
u
u
t
u A t t
w
w w

 =


 =

=  
A and B are found from
initial conditions

66. Tn =natural period of vibration
 ωn =natural circular
frequency of
vibration
n
k
m
w =
2
n
n
T

w
=
fn =1/Tn= natural cyclic frequency of vibration in
hertz (cycles per second)
Undamped free response for SDOF systems:

67. Solving initial conditions
0
. .
0
.
0
0
( 0)
( 0)
cos sin
n
n n
n
u t u A
u t u B
u
u u t t
w
w w
w
= = =
= = =
= 
cos sin
n n
u A t t
w w
=  

68. Example 1

69. Example 1 (continued)

70. Example 1 (continued)

By analogy
By analogy

71. Example 2

72. Example 2 (continued)
From equilibrium

73.  Thus:
Example 2 (continued)

74. Group Solving problem

75.  Draw FBD
 Write equation of motion

76.  Use analogy

78. Energy method
Example 1

81. Energy methods: Example 2

84. Undamped forced vibrations

85. Free Body Diagram


86. Equilibrium Equation
2
2
2
2
( )
( )
u
F t ku m
t
u
m ku F t
t

 =


 =


87. Solution for constant loading
2
2
2
2
2
/
cos sin /
n
n n
u
m ku P
t
u
u P m
t
u A t t P k

 =


 w =

= w   w 

88. Solving initial conditions
.
0
0
max
0, 0 0
0, 0 /
(1 cos )
2 / 2
n
static
t u B
t u A P k
P
u t
K
u P K u
= = 
 =
= = 
 = 
=  w
= =
cos sin /
u A t t P k
= w  w 

89. Sine curve
..
2
2
sin
1
cos sin sin
1 ( )
1
1 ( )
o
n n o
o
n
o
n
mu ku F t
F
u C t D t t
k
DMF
w
w
w
w
 =
= w  w 

w
=

w

90. 90
Viscous Damped free vibration :
x
m
x
c
kx
F 

 =


=

0
=

 kx
x
c
x
m 


0
2 2
=

 x
x
x n
n w
w 


k
c
m
x
0
=
x
)
(dashpot
n
m
c
zeta
w

2
)
( 
c : viscous damping constant (in N s/m)
Define: viscous damping factor (no unit)
0
2 2
2
=

 n
n w

w

Use a trial solution x = A et :
Obtain two possible ’s :
)
1
( 2
1 




w
=
 n )
1
( 2
2 




w
=
 n
and
t
t
e
A
e
A
x 2
1
2
1



=
t
e 1
λ t
e 2
λ
are two solutions.
General solution is a linear combination
and

91. 91
Case 1 :  > 1 (overdamping) :
1 and 2 < 0
t
t
e
A
e
A
x 2
1
2
1





=
x decays to zero without oscillation
t
x
1,
>
 overdamped
1
=

Critical
damped
1
<
 underdamping
Three cases:

92. 92
Case 2:  = 1 (critical damping) :
1 = 2 = -wn
A1 exp(-wnt) is a solution
A2 t exp(-wnt) is also a solution (prove !)
The general solution is x = (A1 + A2 t )exp(-wnt)
x approaches zero quickly without oscillation.

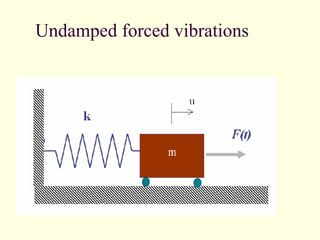
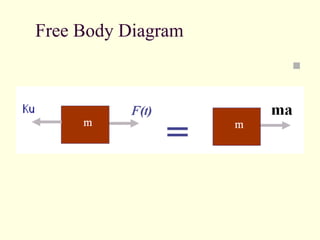
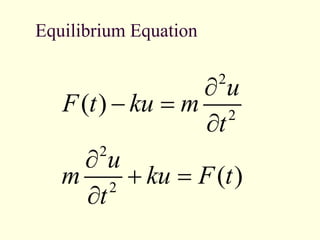
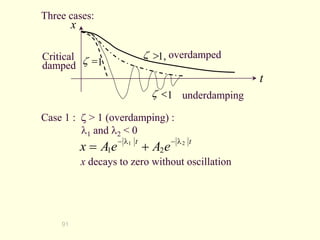
93. 93
Case 3: < 1 (underdamping) :
t
t
i
t
i n
n
n
e
e
A
e
A
x w

w



w




= )
(
2
2
1
2
1
1
2
1 
w
w 
= n
d
Define damped natural frequency
d

1
x 2
x
1
t 2
t
x
t
)
sin(
)
(
]
e
2
2
and
e
2
1
Let
conjucate.
complex
are
2
and
1
that
so
real,
is
[
)
( 2
1


w
w

=


=

=
w

w

w

=
t
d
t
n
Ce
x
i
C
A
i
C
A
A
A
x
t
t
i
t
i n
d
d
e
e
A
e
A
x
Period d = 2/wd

94. 94
 
2
2
2
1
1
2
1
2
/
decrement
c
logarithmi
Define



=


w

w
=

w
=



n
n
d
n
x
x
n

It is because  = c/(2mwn), measurement of  determines
the viscous damping constant c.
d
n
d
n
n
e
Ce
Ce
x
x
t
t

w

w
w
=
= 


)
(
2
1
1
1
cycles
successive
two
of
nts
displaceme
the
of
ratio
The

95. 95
x
m
t
F
x
c
kx
F o 

 =



=
 w
sin
B. Viscous Damped Forced vibration
The equation of motion :
t
F
kx
x
c
x
m o w
sin
=


 


t
m
F
x
x
x o
n
n w
w
w sin
2 2
=

 


k
c
m
x
0
=
x
)
(dashpot
t
F
F O w
sin
=
)
(spring

96. 96
 
   
 
 
 
   
  2
/
1
2
2
2
2
2
/
1
2
2
2
/
2
/
1
/
1
/
factor
ion
magnificat
or
ratio
amplitude
Define
/
1
/
2
tan
/
2
/
1
/
n
n
o
n
n
n
n
o
k
F
C
M
k
F
C
w
w
w
w
w
w
w
w

w
w
w
w


=
=

=


=
)
sin(
and
)
cos(
then
),
sin(
Let
2

w
w

w
w

w


=

=

=
t
C
x
t
C
x
t
C
x
p
p
p



t
m
F
x
x
x o
n
n w
w
w sin
2 2
=

 



97. 97
M
n
w
w /
1
1
0
=

1
.
0
=

2
.
0
=

1
=

Maximum M occurs at: 0
}
)
2
(
]
)
(
1
{[
d
d 2
2
2 =


n
n w
w
w
w
w
n
res w

w 2
1 2

=
The resonance frequency is

98. 98
n
w
w /
1
)
(resonance
0
=

2
.
0
=

1
=

0
2
/



Consider the following regions:
(1) w is small, tan > 0,   0+, xp in phase with the driving force
(2) w is large, tan < 0,   0-,  = , xp lags the driving force by 90o
(3) w  wn
-, tan +,   /2(-)
w  wn
+, tan -,   /2(+)
tan  = 2
n
n
)
(ww


ww


99. 99
If the driving force is not applied to the mass, but is
applied to the base of the system:
t
sin
2 2
2
n
n w
w
=
w

w
 b
x
x
x 


If bw2 is replaced by Fo/m:
)
( B
x
x
m
kx
x
c 



 
=


k
c
x
0
=
x
t
b
xB w
sin
=
m
t
sin
2 2
n
n w
=
w

w

m
F
x
x
x o



This can be used as a device to detect earthquake.
B
x
m
kx
x
c
x
m 



 
=



100. 100
Determine : (a) steady-state displacement
(b) max. force transmitted to the base.
k c
m
p
A
m =45 kg, k = 35 kN/m,
c = 1250 N.s/m,
p = 4000 sin (30 t) Pa,
A= 50 x 10-3 m2.
Example
)
(
498
.
0
)
9
.
27
45
2
/(
1250
)
2
/(
/
9
.
27
45
/
10
35
/ 3
d
underdampe
m
c
s
rad
m
k
n
n
=


=
=
=

=
=
w

w

101. 101
The amplitude of the steady-state vibration is:
 
   
 
   
m
n
n
k
o
F
X
00528
.
0
2
/
1
2
79
.
2
/
30
498
.
0
2
2
2
9
.
27
/
30
1
3
10
35
/
3
10
50
4000
2
/
1
2
/
2
2
2
/
1
/
=








=


=











 w
w
w
w
   
rad
n
n
716
.
1
2
9
.
27
/
30
1
9
.
27
/
30
498
.
0
2
1
tan
2
/
1
/
2
1
tan =




=


= 











w
w
w
w

#
)
716
.
1
30
cos(
00528
.
0
)
cos( m
t
t
X
xP 
=

= 
w

102. 102
The force transmitted to the base is :
)
(
cos
)
(
sin 
w
w

w 


=

=
t
X
c
t
kX
x
c
kx
F p
p
tr 
For max Ftr :
  k
c
t
t
d
dFtr w

w

w
1
tan
0 
=


=

o
3
3
1
9
.
46
10
35
10
3035
1250
tan =



=

 

wt
 
#
o
o
3
max
271
9
.
46
sin
00528
.
0
30
1250
9
.
46
cos
00528
.
0
10
35
N
Ftr
=





=


104. Newton Laws, Energy
Theorems and Momentum
Principles
Integration Principles

105. Group Working Problems
Problem 1: Chapters 17, 18 and 19
Given: The 30-kg disk is pin
connected at its center. If it
starts from rest,
Find:
the number of revolutions it must
make and the time needed to
attain an angular velocity of
20rad/s?

106. Problem 1: Newton Laws
 Find angular acceleration: (11.7rad/s2)
 Find angle (17.1 radians)
 Find number of revolutions: (2.73)
 Find time (1.71 sec)

107. Problem 1: Energy Theorems
 Find angle (17.1 radians)
 Find number of revolutions: (2.73)
 Find angular acceleration: (11.7rad/s2)
 Find time (1.71 sec)

108. Problem 1: Momentum Principle
 Find time (1.71 sec)
 Find angular acceleration: (11.7rad/s2)
 Find angle (17.1 radians)
 Find number of revolutions: (2.73)

109. Problem 2: Chapter 22 in view of Chapters
17, 18 and 19
 Given: a 10-kg block
suspended from a cord
wrapped around a 5kg
disk.
 Find: natural period of
vibration

110. Problem 2: Newton Laws
 Find differential equation
 Find period (1.57s)

111. Problem 2: Energy Theorems: use
conservation of energy
 Write conservation of energy equation
 Differentiate equation
 Find period (1.57s)

112. Problem 2: Momentum Principle: use
M=d(HG)/dt
 Write M=d(HG)/dt for a displacement θ from
equilibrium position
 Differentiate equation
 Find period (1.57s)