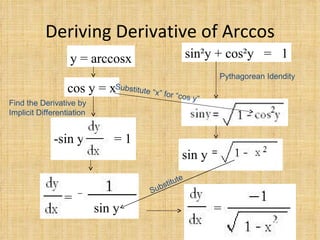
1) The document discusses the derivatives of inverse trigonometric functions arcsin, arccos, and arctan. 2) It provides the steps to derive the derivatives of these functions using implicit differentiation and trigonometric identities like Pythagorean identities. 3) The document also mentions that according to the Fundamental Theorem of Calculus, the integrals of inverse trigonometric functions can be found by taking the antiderivative of their derivatives. It provides some examples of problems to solve.

1. Arcsin, Arccos, Arctan Paul Nettleton

2. Derivatives of Inverse trigonometric functions

3. Deriving Derivative of Arcsin sin²y + cos²y = 1 y = arcsinx sin y = x Pythagorean Idendity Find the Derivative by Implicit Differentiation cos y = 1 = Substitute Substitute “x” for “sin y”

4. Deriving Derivative of Arccos sin²y + cos²y = 1 y = arccosx cos y = x Pythagorean Idendity Find the Derivative by Implicit Differentiation -sin y = 1 Substitute “x” for “cos y” = _ sin y = sin y Substitute

5. Deriving Derivative of Arctan y = arctan x tan y = x Find the Derivative by Implicit Differentiation sec ² y = 1 A = sec ² y 1 Substitute A = 1 + tan²y 1 Substitute “x” for “tan y” 1 + tan²y = sec²y Pythagorean Identity

6. Integrals of Inverse Trigonometric Functions According to the Fundamental Theorem of Calculus

7. Try Some Problems! d dx = Click to view Answers Source: http://www.themathpage.com/acalc/inverse-trig.htm#arcsin d dx arcsin x ² = d dx x ² arcsin x =

8. Harder Problems d dx 3 arccos( x 2 + 0.5) 4 arctan3 x 4 d dx Click to view Answers Source: http://www.intmath.com/Differentiation-transcendental/3_Derivative-arcsin-arccos-arctan.php