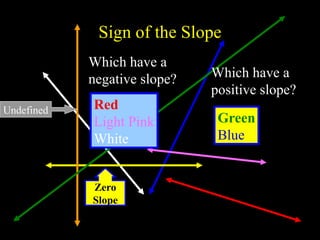
The document discusses the concept of lines, slopes, and their applications within analytic geometry, emphasizing the calculation of slope between points and the properties of parallel and perpendicular lines. It also introduces real-world applications of slope, such as road grades, wheelchair ramps, and architecture. Additionally, it provides methods for writing equations of lines based on given points or slopes and explains related concepts such as slope-intercept form and the characteristics of horizontal and vertical lines.

1. What is a Line?
• A line is the set of points forming a straight
path on a plane
• The slant (slope) between any two points on
a line is always equal
• A line on the Cartesian plane can be
described by a linear equation
x-axis
y-axis

2. MATM 603 - Analytic Geometry
Topic: Slope of a Line, Parallel
and Perpendicular Lines
(Examples and Applications)
Marjorie M. Estuita
Discussant
Dr. Allan Quismundo
Professor

3. Slope
Slope describes the
direction of a line.

4. Guard against 0 in
the denominator
Slope
If x1  x2, the slope of the line
through the distinct points P1(x1, y1)
and P2(x2, y2) is:
1
2
1
2
x
x
y
y
x
in
change
y
in
change
run
rise
slope





Why is
this
needed
?

5. x-axis
y-axis
Find the slope between (-3, 6) and (5, 2)
Rise
Run
-4
8
-1
2
= =
(-3, 6)
(5, 2)

6. Calculate the slope between (-3, 6) and (5, 2)
1
2
1
2
x
x
y
y
m



)
3
-
(
)
5
(
)
6
(
)
2
(



m
8
4
-

2
1
-

x1 y1 x2 y2
We use the letter m
to represent slope
m

7. Find the Slopes
(5, -2)
(11, 2)
(3, 9)
1
2
1
2
x
x
y
y
m



3
11
9
2
1



m
Yellow
5
11
)
2
-
(
2
2



m
Blue
3
5
9
2
-
3



m
Red
8
7
-

3
2

2
11
-


8. Find the slope between (5, 4) and (5, 2).
1
2
1
2
x
x
y
y
m



)
5
(
)
5
(
)
4
(
)
2
(



m
0
2
-

STOP
This slope is undefined.
x1 y1 x2 y2

9. x
y
Find the slope between (5, 4) and (5, 2).
Rise
Run
-2
0
Undefined
= =

10. Find the slope between (5, 4) and (-3, 4).
1
2
1
2
x
x
y
y
m



)
5
(
)
3
-
(
)
4
(
)
4
(



m
8
-
0

This slope is zero.
x1 y1 x2 y2
0


11. x
y
Rise
Run
0
-8
Zero
= =
Find the slope between (5, 4) and (-3, 4).

12. From these results we
can see...
•The slope of a vertical
line is undefined.
•The slope of a
horizontal line is 0.

13. Find the slope of the line
4x - y = 8
)
0
(
)
2
(
)
8
-
(
)
0
(



m
2
8

Let x = 0 to
find the
y-intercept.
8
-
8
-
8
)
0
(
4




y
y
y Let y = 0 to
find the
x-intercept.
2
8
4
8
)
0
(
4




x
x
x
(0, -8) (2, 0)
4

First, find two points on the line
x1 y1 x2 y2

14. Find the slope of the line
4x  y = 8 Here is an easier way
Solve
for y.
8
4 
 y
x
8
4
-
- 
 x
y
8
4 
 x
y
When the equation is solved for y the
coefficient of the x is the slope.
We call this the slope-intercept form
y = mx + b
m is the slope and b is the y-intercept

15. x
y
Graph the line that goes through (1, -3) with
(1,-3)
4
3
-

m

16. Sign of the Slope
Which have a
positive slope?
Green
Blue
Which have a
negative slope?
Red
Light Pink
White
Undefined
Zero
Slope

17. Slope of Parallel Lines
• Two lines with the
same slope are parallel.
• Two parallel lines have
the same slope.

18. Are the two lines parallel?
L1: through (-2, 1) and (4, 5) and
L2: through (3, 0) and (0, -2)
)
0
(
)
3
(
)
2
-
(
)
0
(
2



m
)
2
-
(
)
4
(
)
1
(
)
5
(
1



m
6
4

3
2

3
2

2
1
2
1
L
L
m
m


This symbol means Parallel

19. x
y
Perpendicular Slopes
4
3
-
1 
m
3
4
2 
m
4
3
What can we say
about the intersection
of the two white lines?

20. Slopes of Perpendicular Lines
• If neither line is vertical then the slopes of
perpendicular lines are negative reciprocals.
• Lines with slopes that are negative
reciprocals are perpendicular.
• If the product of the slopes of two lines is -1
then the lines are perpendicular.
• Horizontal lines are perpendicular to
vertical lines.

21. Write parallel, perpendicular or neither for the
pair of lines that passes through (5, -9) and (3, 7)
and the line through (0, 2) and (8, 3).
)
5
(
)
3
(
)
9
-
(
)
7
(
1



m
)
0
(
)
8
(
)
2
(
)
3
(
2



m
2
-
16
 8
-

8
1
 





1
8
-






8
1
8
8
-
 1
-

2
1
2
1 1
-
L
L
m
m




This symbol means Perpendicular

22. MATM 603 - Analytic Geometry
Topic: Slope of a Line, Parallel
and Perpendicular Lines
(Examples and Applications)
Marjorie M. Estuita
Discussant
Dr. Allan Quismundo
Professor

23. Application
To represent the grade of a road,
numbers like 3%, 5%, 8% and
15% are used. Such a number
tells you how steep a road is on a
hill or mountain.
Recall that slope = m = rise /
run
Real-world applications of
slope, just to mention a few,
are the grade of a road,
wheelchair ramp for the
handicapped, and roof pitch.

24. Application
Suppose that the rise and the run are
measured in feet. Then, a 15% grade
means that the road rises 15 feet for
every horizontal distance of 100 feet.
Slope = grade of the road
= rise / run = 15 / 100 = 15%
A 15% grade is not very steep, but the
authorities may decide that this is steep
enough to alert drivers.

25. Application
Slope and ramp for the handicapped
According to construction laws, the ramp for the handicapped
should never exceed a slope or grade of 8.333%.
8.333% = 8.333 / 100 = (8.333 ÷ 8.333) / (100 ÷ 8.333) = 1 /
12.00048
Therefore, an 8.3% grade means that for every horizontal run
of 12 feet, there should be a vertical rise of 1 foot.

26. Application
Slope and roof pitch of a house
The roof pitch, also called roof
slope, is simply the steepness of
the roof of a house. The roof pitch
can be found by looking for the
number of inches the roof rises
vertically for every 12 inches of
horizontal run.

27. Application
A roof pitch of 3/12 means that the
roof rises 3 inches for every 12
inches of horizontal run.
The roof pitch depends on the
material, such as asphalt, you put
on the roof. One material may
require a roof pitch of 3/12 while
other materials may a roof pitch
that is more or less.

28. Application
Architecture, An architect uses
software to design the ceiling of a
room. The architect needs to enter an
equation that represents a new beam.
The new beam will be perpendicular
to the existing beam, which is
represented by the red line. The new
beam will pass through the corner
represented by the blue point. What is
the equation that represents the new
beam?

29. Existing Beam
Sol:
Step1:
Use the slope formula to find the slope of the red line
that represents the existing beam.
m =4-6/6-3
= – 2/3
The slope of the line that represents the existing beam is
= – 2/3.

30. Step2:
Find the opposite reciprocal of the slope
from step 1.
The opposite reciprocal of -2/3 is 3/2
Step3:
Use the point-slope form to write an
equation. The slope of the line that
represents the new beam is 3/2.
It will pass through (12, 10)
An equation that represents the new beam
is
y-10 = 3/2x-12

31. Application
Parallel and perpendicular lines have various
applications in real-life scenarios. Here are some
examples:
1. *Construction*:
Parallel lines are used in constructing structures
like buildings, bridges, and roads. Ensuring that
lines are parallel is crucial for structural integrity
and aesthetics.
2. *Cartography*:
On maps, parallel lines represent latitude, while
meridians represent longitude. These lines help in
locating places on the Earth's surface accurately.

32. Application
3. *Art and Design*:
Artists and designers use parallel and
perpendicular lines to create shapes, patterns, and
structures in their work. These lines help in
achieving balance and symmetry.
4. *Architecture*:
In architecture, parallel lines are used in the design
of facades and other structural elements.
Perpendicular lines are often seen in the framing of
doors, windows, and other architectural features.

33. Application
5. *Engineering*:
Parallel and perpendicular lines are used in the
design and construction of machinery, equipment,
and structures. They help in ensuring accuracy and
precision in measurements and alignments.
6. *Graphic Design*:
In graphic design, parallel and perpendicular lines
are used to create visual interest, guide the viewer's
eye, and establish a sense of order and structure.

34. Application
7. *Road Design*:
Roads and highways often have parallel lanes and
perpendicular intersections, which help in traffic
management and safety.
8. *Textiles and Fabric Design*: Patterns in textiles
often use parallel and perpendicular lines to
create visual effects and designs.

35. Application
9. *Geometric Drawing*:
In geometric drawing, parallel and perpendicular
lines are used to represent three-dimensional
objects on a two-dimensional plane.
10. *Computer Graphics*:
In computer graphics, parallel and perpendicular
lines are used to create models, animations, and
visual effects.

36. Parallel and Perpendicular Lines
in Real Life

37. Parallel and Perpendicular Lines
in Real Life

38. Understanding the properties of
slope, parallel and perpendicular
lines is essential in these and many
other fields where precision and
accuracy are important.

39. Thank you for
listening and
have a blessed
day to all

40. The Equation of a Line

41. Objectives
• Write the equation of a line, given its
slope and a point on the line.
• Write the equation of a line, given two
points on the line.
• Write the equation of a line given its
slope and y-intercept.

42. Objectives
• Find the slope and the y-intercept of a
line, given its equation.
• Write the equation of a line parallel or
perpendicular to a given line through a
given point.

43. Slope-intercept Form
Objective
Write the equation of a line, given its slope
and a point on the line.
y = mx + b
m is the slope and b is the y-intercept

44. Write the equation of the line
with slope m = 5 and y-int -3
Take the slope intercept form y = mx + b
Replace in the m and the b y = mx + b
y = 5x + -3
y = 5x – 3
Simplify
That’s all there is to it… for this easy question

45. Find the equation of the line
through (-2, 7) with slope m = 3
Take the slope intercept form y = mx + b
Replace in the y, m and x y = mx + b
7 = mx + b
x y m
7 = 3x + b
7 = 3(-2) + b
7 = -6 + b
Solve for b
7 + 6 = b
13 = b
Replace m and b back into
slope intercept form y = 3x + 13

46. Write an equation of the line
through (-1, 2) and (5, 7).
First calculate the slope.
b

 )
1
-
(
2 6
5
1
2
1
2
x
x
y
y
m



)
1
-
(
5
2
7



6
5

Now plug into y, m and x into
slope-intercept form.
(use either x, y point)
Solve for b
Replace back into slope-intercept form
b
mx
y 

b

 6
5
-
2
b

 6
5
2
b

6
17
6
17
6
5 
 x
y
Only replace
the m and b

47. Horizontal and
Vertical Lines
• If a is a constant,
the vertical line
though (a, b) has
equation x = a.
• If b is a constant,
the horizontal line
though ( a, b,) has
equation y = b.
(a, b)

48. Write the equation of the line
through (8, -2); m = 0
2
-

y
Slope = 0 means the line is horizontal
That’s all there is!

49. Find the slope and
y-intercept of
2x – 5y = 1
Solve for y and
then we will be
able to read it from
the answer.
1
5
2 
 y
x
y
x 5
1
2 

y
x 

5
1
5
2
5
1
x
5
2
y 

5
2

m
5
1
-
5 5 5
Slope: y-int:

50. Write an equation for the line
through (5, 7) parallel to 2x – 5y = 15.
5
2

m
15
5
2 
 y
x
y
x 5
15
2 

5
5
5
15
5
2 y
x


y
x 
 3
5
2

51. We know the slope and
we know a point.
)
7
,
5
(
5
2

m
b

 )
5
(
7 5
2 b
mx
y 

7 = 2 + b
7 – 2 = b
5 = b
5
5
2 
 x
y
Write an equation for the line
through (5, 7) parallel to 2x – 5y = 15.

52. 3
5
2

 x
y
5
5
2

 x
y
Write an equation for the line
through (5, 7) parallel to 2x – 5y = 15.
15
5
2 
 y
x

53. The slope of the perpendicular.
• The slope of the perpendicular line is the
negative reciprocal of m
• Flip it over and change the sign.
3
2
Examples of slopes of perpendicular lines:
-2
5
1
2
7
-
2.4
Note: The product of perpendicular slopes is -1
2
3
1
5
= -5 -2
1 2
1
 12
5
-7
2 7
2


54. What about the special cases?
• What is the slope of
the line perpendicular
to a horizontal line?
1
0

Well, the slope of a
horizontal line is 0…
So what’s the negative
reciprocal of 0?
0
0
1
Anything over
zero is undefined
The slope of a line
 to a horizontal
line is undefined.

55. Write an equation in for the line through (-8, 3)
perpendicular to 2x – 3y = 10.
We know the perpendicular
slope and we know a point.
3
2

slope
)
3
,
8
-
(
2
3
-
2 
m
Isolate y to find the slope: 2x – 3y = 10
2x = 10 + 3y
2x – 10 = 3y
3 3 3
b

 )
8
-
(
3 2
3
- b
mx
y 

3 = 12 + b
3 – 12 = b
-9 = b
9
2
-3
: 
 x
y
answer

56. Write an equation in standard form for the
line through (-8, 3) perpendicular to
2x - 3y = 10.
3
10
3
2

 x
y
9
2
3
-

 x
y

57. Summary
b
mx
y 

• Slope-intercept form
• y is isolated
• Slope is m.
• y-intercept is (0, b)

58. Summary
• Vertical line
–Slope is undefined
–x-intercept is (a, 0)
–no y-intercept
• Horizontal line
–Slope is 0.
–y-intercept is (0, b)
–no x-intercept
a
x 
b
y 