1) Plastic analysis was performed using the lower-bound theorem and equilibrium method to determine the collapse load of a W30x99 beam with continuous lateral support. 2) The working load was first determined by calculating the yield moment My. Once yielding occurred, the plastic moment capacity Mp was used. 3) Equilibrium of internal and external moments was satisfied at the collapse mechanism to determine the ultimate load. The uniqueness theorem confirmed this was the collapse load.

1. T.Chhay
Appendix A. karKNna nigkarviPaKedaylkçN³)aøsÞic
Plastic Analysis and Design
A >1> esckþIepþIm Introduction
eyIg)anENnaMBIKMniténkar)ak;eday)aøsÞic (plastic collapse) enAkñúgEpñk 5>2/ “ kugRtaMg
Bt; nigm:Um:g)aøsÞic” . kar)ak;rbs;eRKOgbgÁúMnwgekIteLIgenAeBlbnÞúkbegáItsnøak;)aøsÞicRKb;RKan;edIm,I
;
begáItCa mechanism EdlnwgeFVIeGaymanPaBdabedayminmankarekIneLIgbnÞúk. enAkñúgFñwmEdl
kMNt;edaysþaTic eKRtUvkarEtsnøak;)aøsÞicmYyEtb:ueNÑaH. dUcbgðajenAkñúgrUbTI A>1 snøak;nwgekIt
manenAkEnøgNaEdlmanm:Um:g;Gtibrma ¬krNIenHKWenAkNþalElVg¦. enAeBlEdlm:Um:g;Bt;mantMél
FMRKb;RKan;edIm,IeFVIeGaymuxkat;TaMgmUl yield/ enaHvaminGacTb;nwgkarekIneLIgrbs;m:Um:g;EfmeTot/
ehIysnøak;)aøsÞick¾RtUv)anbegáIteLIg. snøak;)aøsÞicenHRsedogKñanwgsnøak;FmμtaEdr EtxusRtg;fa
snøak;)aøsÞicmanlT§PaBTb;nwgm:m:g;xøH EdldUcKñay:agxøaMgnwg rusty hinge.
U
460 Appendix A

2. NPIC
lT§PaBm:Um:g;)aøsÞic (plastic moment capacity) EdlsMKal;eday M p Cam:Um:g;Bt;EdlekIt
manenARtg;snøak;)aøsÞic. vamantMélesμInwgm:Um:g;Tb;xagkñúgEdlekItBIkarEbgEckkugRtaMgEdlbgðaj
enAkñúgrUbTI A>1 c EtmanTisedApÞúyKña. eKGackMNt;m:Um:g;)aøsÞicenAeBlEdleKsÁal; yield stress
nigrUbragmuxkat; dUcbgðajenAkñúgrUbTI A>2. RbsinebIkarEbgEckkugRtaMgenAkñúglkçxNÐ)aøsÞiceBj
RtUv)anCMnYsedaykMlaMgsmmUlsþaTicBIrEdlmantMéldUcKña nigTisedApÞúyKña enaHvanwgbegáIt couple.
GaMgtg;sIueténkMlaMgnImYy²esμInwgplKuNrvag yield stress nigBak;kNþalRkLaépÞmuxkat;srub.
m:Um:g;EdlbegáIteday couple xagkñúgenHKW
A
M p = Fy a = Fy Z x
2
Edl A CaRkLaépÞmuxkat;srub/ a CacMgayrvagTIRbCMuTMgn;énRkLaépÞBak;kNþalBIr nig Z x Cam:U
Dulmuxkat;)aøsÞic. emKuNsuvtßiPaBcenøaHsßanPaB yielding dMbUg nigsßanPaB)aøsÞiceBjRtUv)ansM
EdgenAkñúgm:UDulmuxkat;. BIrUbTI A>1 b eKGacsresrm:Um:g;EdlbegáIt yield dMbUg
M p Fy Z x Z x
M y = Fy S x nig = =
M y F S
y x xS
pleFobenHCatMélefrsMrab;rUbragmuxkat;EdlsÁal; nigRtUv)aneKehAfa emKuNrUbrag. sMrab;Fñwm
EdlKNnaeday allowable stress theory vaCargVas;én reserve capacity ehIymantMélmFüm 1.12
sMrab; W-shapes.
enAkñúgFñwm b¤eRKagsþaTicminkMNt; eKRtUvkarsnøak;)aøsÞiceRcInCagmYyedIm,IbegáIt collapse
mechanism. snøak;TaMgenHnwgRtUv)anbegáIttamlMdab;lMeday eTaHbICaeKmincaM)ac;dwgBIlMdab;k¾eday.
eKnwgBicarNakarviPaKrcnasm<n§½sþaTicminkMNt;eRkayBIkarBiPakSatMrUvkarrbs; Specification.
461 Appendix A

3. T.Chhay
A>2> AISC Requirements
AISC Specification GnuBaØatieGayeRbI plastic analysis and design enAeBl eRKOg
bgÁúMenArkSaPaBlMnwgTaMg local nigTaMgmUl Rtg;cMnuc plastic collapse. edaysareKtMrUveGayFñwm
b¤eRKagrgnUvPaBdabFMenAeBlEdlsnøak;)aøsÞicRtUv)anbegáIt eKRtUvkar lateral bracing CaBiess.
edIm,IkarBar local buckling, AISC B5.2 TamTarfaGgát;man compact cross-sectional
shape Edl λ ≤ λ p sMrab;TaMgRTnug nigsøab. sMrab;Ggát; I-shaped shape dUcCa W nig S-shapes
pleFobTTwgelIkMras;EdlkMNt;BI Table B5.2 KW
bf 65 bf 170
≤ (US) ≤ (IS)
2t f Fy 2t f Fy
nig h
tw
≤
640
Fy
(US)
h 1680
tw
≤
Fy
(IS)
edIm,IkarBar lateral buckling, AISC F1.2d kMNt; unbraced length Gtibrma Lb Rtg;
TItaMgsnøak;)aøsÞicCa L pd EdlsMrab; I-shaped member
3600 + 2200(M 1 / M 2 )
L pd = ry (US) (AISC Equation F1-17)
Fy
24820 + 15170(M 1 / M 2 )
L pd = ry (IS)
Fy
enAkñúgsmIkarenH M 1 Cam:Um:g;EdltUcCagenARtg;cugén unbraced length nig M 2 CamU:m:g;EdlFMCag.
pleFob M 1 / M 2 KwviC¢manenAeBlEdl M 1 nig M 2 Bt;Ggát;eGaymankMeNagDub nigmantMél
GviC¢manenAeBlEdlvabegáItkMeNageTal.
sMrab; compact shape Edlman lateral bracing RKb;RKan; eKGacyk M n esμInwg M p sMrab;
eRbIenAkñúg plastic analysis. b:uEnþ AISC F1.2d kMNt;faenAkñúgtMbn;EdlekItmansnøak;)aøsÞiccug
eRkay nigenAkñúgtMbn;EdlminEk,rsnøak;)aøsÞic eKRtUveRbIviFIFmμtaedIm,IkMNt; M n .
AISC Specification provision epSgeTotEdlTak;Tgnwg plastic analysis and design
mandUcxageRkam.
A5.1 Plastic analysis RtUv)anGnuBaØatsMrab;Et Fy ≤ 65ksi .
C2.2 kMlaMgtamG½kSEdlbegáItedaybnÞúkTMnajemKuN nigbnÞúktamTisedkemKuNminRtUvFM
Cag 0.75φc Ag Fy .
462 Appendix A

4. NPIC
E1.2 sMrab;ssr slenderness parameter λc minRtUvFMCag 1.5K Edl K CaemKuNRbEvg
RbsiT§PaB.
A >3> karviPaK Analysis
RbsinebIvaGacman collapse mechanism eRcInCamYy dUcCaFñwmCab;EdlbgðajenAkñúgrUbTI A>3
eKGacrk)annUv collapse mechanism EdlRtwmRtUv ehIyviPaKCamYynwgCMnYyénRTwsþIeKalcMnYnbIrbs;
plaxtic analysis EdleGayenATIenHedayKμankarRsaybBa¢ak;.
!> Lower-bound theorem (static theorem): RbsinebIeKGacrk)annUvkarEbgEck
m:Um:g;d¾mansuvtßiPaB ¬Edlm:Um:g;mYytUcCag b¤esμInwg M p RKb;kEnøg¦ ehIyvaGacTTYl
bnÞúkedaysþaTic ¬lMnwgRtUv)anbMeBj¦ bnÞab;mkbnÞúkEdlRtUvKñaRtUvtUcCag b¤esμI
collapse load.
@> Upper-bound theorem (kinetic theorem): bnÞúkEdlRtUvnwg mechanism snμt;RtUvEtFM
Cag b¤esμInwg collapse load. Cavi)ak RbsinebIeKGegát mechanism EdlGacmanTaMg
Gs; mechanism mYyNaEdlRtUvkarbnÞúktUcCageKCa mechanism EdlRtwmRtUv.
#> Uniqueness theorem: RbsineKmankarEbgEckm:Um:g;EdlGacTTYlyk)anedaysþaTic
nigmansuvtßiPaB EdlenAkñúgenaH snøak;)aøsÞicRKb;RKan;begáIt collapse mechanism enaH
463 Appendix A

5. T.Chhay
bnÞúkEdlRtUvKñaCa collapse load EdlRbsinebI mechanism bMeBjTaMg upper-boud
theorem nig lower-bound theorem vaCa mechanism EdlRtwmRtUv.
karviPaKEdlQrelI lower-bound theorem RtUv)aneKehAfa equilibrium method ehIyRtUv)an
bgðajenAkñúg]TahrN_ A>1.
]TahrN_ A>1³ rkbnÞúkcugeRkay (ultimate load) sMrab;FñwmEdlbgðajenAkñúgrUbTI A>4a eday
equilibrium method rbs; plastic analysis. snμt;eKeRbI continuous lateral support nig EdlRb
ePT A36 .
dMeNaHRsay³ Edk A36 muxkat; W 30 × 99 Ca comapact shape ehIyCamYynwg continuous lateral
support, tMrUvkar lateral bracing KWRKb;RKan; dUcenHeKGacTTYlyk plastic analysis.
dMNak;karénkardak;bnÞúkelIFñwm BI working load eTAdl; collapse load
RtUv)anKUsbBa¢ak;enAkñúgrUbTI A>4a-d. enAeBl working load muneBl yielding ekIteLIgRKb;TIkEnøg
karEbgEckm:Um:g;Bt;RtUv)anbgðajenAkñúgrUbTI A>4a CamYynwgm:Um:g;GtibrmaEdlekItmanRtg;TMrbgáb;.
enAeBlEdlbnÞúkekIneLIgbnþicmþg² yielding cab;epþImekItmanRtg;TMr enAeBlEdlm:Um:g;Bt;eTAdl;
M y = Fy S x . enAeBlEdlbnÞúkekIneLIgkan;EtFM vanwgekItmansnøak;)aøsÞickñúgeBldMNalKñaenA
Rtg;cugnImYy² enAeBlEdl M p = Fy Z x . enARtg;kMrwténkardak;bnÞúkenH eRKOgbgÁúMenAmanesßrPaB
464 Appendix A

6. NPIC
enAeLIy FñwmRtUv)anERbkøayeTACasþaTickMNt;edaykarekItmansnøak;)aøsÞicBIr. Mechanism nwgekIt
anEtenAeBlEdlekItmansnøak;)aøsÞicTIbI. vaGacekItmanenAeBlEdlm:Um:g;viC¢manGtibrmamantMél
M p . edayGaRs½ynwg uniqueness theorem/ bnÞúkEdlRtUvKñaCa collapse load BIeRBaHkarEbgEck
m:Um:g;KWsuvtßiPaB ehIyGacTTYlyk)anedaysþaTic.
enARKb;tMNak;kalénkardak;bnÞúk plbUkénéldac;xaténm:Um:g;viC¢man nigm:Um:g;GviC¢manGti-
brmaKW wL2 / 8 . enAeBl collapse, plbUkenHkøayeTACa
16M p
M p + M p = wu L2 b¤
1
wu =
8 L2
eKRtUvEteRbobeFobbnÞúkemKuNCamYynwgersIusþg;emKuN dUcenHeKeRcIneRbI φb M p Cag M p enAkñúg
smIkarBIxagedIm. b:uEnþedIm,IrkSanimitþsBaØaeGaymanlkçN³samBaØ eyIgeRbI M p enARKb;]TahrN_
TaMgGs;rhUtdl;CMhancugeRkayeTIbeyIgCMnYs φb M p eTAkñúgsmIkar. lT§plEdlRtwmRtUv
sMrab;]TahrN_enHKW
16φb M p
wu =
L2
sMrab; W 30 × 99
36(312 )
M p = Fy Z x = = 936 ft − kips
12
ehIy φb M p = 0.9(936) = 842.4 ft − kips
eKk¾GacTTYltMélrbs; φb M p edaypÞal;BI Load Factor Design Selection Table enAkñúg Part 4 of
the Manual.
16(842.4 )
cemøIy³ w u =
(30)2
= 15.0kips / ft
]TahrN_ A>2³RbsinebIFñwmenAkñúg]TahrN_ A>1 minman continuous lateral support cUrkMNt;TItaMg
EdlRtUvBRgwg.
dMeNaHRsay³ snøak;)aøsÞicenAxagcugekIteLIgkñúgeBldMNalKña ehIymuneBlsnøak;enAkNþalElVg
ekIteLIg. dUcenHeKKYrEtRtYtBinitü unbraced length GtibrmaedayeFobeTAnwgcug ¬snøak;cugeRkay
EdlekIteLIgmintMrUvkar bracing sMrab; plastic analysis eT¦.
465 Appendix A

7. T.Chhay
edayeFobnwgsnøak;enAcugxageqVg snμt;facMnucBRgwgKWenAkNþalElVg. kñúgkrNIenH M 1 =
M 2 = M p dUcenHFñwmmankMeNagDub ¬m:Um:g;TaMgBIrmansBaØadUcKña¦ dUcenH M 1 / M 2 = +1 BI AISC
Equation F1-17, unbraced length GtibrmaKW
3600 + 2200(M 1 / M 2 ) 3600 + 2200(1.0)
L pd = ry = (2.10) = 338.3in. = 28.2 ft
Fy 36
cMNaMfa FñwmenHesÞIrEtRKb;RKan;edayminRtUvkar lateral bracing.
CamYynwg lateral mYyTl;enAkNþalElVg
L p = 15 ft < 28.2 ft (OK)
Unbraced length EdlRtUvBicarNarYmKWrYbbBa©ÚlTaMgsnøak;enAkNþalElVg. vaminmantMbn;Edlmin
enACab;nwgsnøak;)aøsÞiceT dUcenHvaminRtUvkarkarKNna design strength eT.
cemøIy³ eRbI lateral brace mYyenAkNþalElVg.
Mechanism method KWQrelI upper-bound theoremnigRtUvakrGegátRKb; collapse
mechanism EdlGacekItman. Collapse mechanism NaEdlRtUvkarbnÞúktUcCageKnwglub eyIy
bnÞúkEdlRtUvKñaCa collapse laod. eKRtUvGnuvtþeKalkarN_rbs; virtual work sMrab;viPaK
mechanism nImYy². Mechanism snμt;RtUvrgnUv virtual displacement RsbeTAtamclnaEdl
GacekItmanrbs; mechanism ehIyeKeGaykmμnþxageRkA nigkmμnþxagkñúgesμIKña. bnÞab;mkeKGacrk
TMnak;TMngrvagbnÞúk niglT§PaBTb;m:Um:g;)aøsÞic M p . bec©keTsenHRtUv)anbgðajenAkñúg]TahrN_
A>3 nig A>4.
]TahrN_ A>3³ FñwmCab;EdlRtUv)anbgðajenAkñúgrUbTI A>5 man compact cross section Edlman
design strength φb M p = 1040 ft − kips . eRbI mechanism method edIm,Irk collapse load Pu .
snμt; continuous lateral support.
dMeNaHRsay³ eKman failure mechanism sMrab;FñwmenHBIry:ag. dUcEdlbgðajenAkñúgrUbTI A>5
vamanlkçN³RsedogKñaEdlkMNat;Ggát;nImYy²rgnUv rigid-body motion. edIm,IGegát mechanism
enAkñúgElVg AB dak; vitual rotation θ Rtg; A. karvilEdlRtUvKñaenARtg;snøak;)aøsÞicRtUv)anbgðaj
enAkñúgrUbTI A>5b ehIybMlas;TItamTisQrébnÞúkKW 10θ . BIeKalkarN_rbs; virtual work
kmμnþxageRkA = kmμnþxagkñúg
466 Appendix A

8. NPIC
P(10θ ) = M p (2θ ) + M pθ
¬vaminmankmμnþxagkñúgenARtg; A eT eRBaHvaminmansnøak;)aøsÞic¦
collapse load KW
3M p
Pu =
10
Mechanism sMrab;ElVg AB manlkçN³xusKñabnþic³ RKb;snøak;TaMgbICasnøak;)aøsÞic.
Virtual work xagkñúg nig virtual work xageRkAkñúgkrNIKW
2 Pu (15θ ) = M pθ + M p (2θ ) + M pθ
enaH Pu = 15 M p
2
lT§PaBTIBIrenHRtUvkarbnÞúktUcCag dUcenHvaCa mechanism EdlRtwmRtUv. Collapse load Edlnwg
TTYl)anedayeRbI φb M p CMnYseGay M p
cemøIy³ Pu =
2
15
φb M p = (1040) = 139kips
2
15
467 Appendix A

9. T.Chhay
]TahrN_ A>4³ kMNt; collapse load P sMrab; rigid frame EdlbgðajenAkñúgrUbTI A>6. Ggát;
u
nImYy²rbs;eRKagKW W 21×147 Edlman Fy = 50ksi . snμt; lateral support Cab;.
dMeNaHRsay³ W 21×147 Ca compact shape sMrab; F y = 50ksi nigman lateral support Cab; dUc
enHvabMeBjlkçxNÐkñúgkareRbIR)as; plastic analysis.
dUcbgðajenAkñúgrUbTI A>6 eKman failure mode cMnYnbIsMrab;eRKagenH³ Fñwm mechanism enA
kñúgGgát; BC / sway mechanism nigmYyeTotCabnSMén mechanism BIrdMbUg. eyIgcab;epþImkarviPaK
mechanism nImYy²edaydak; virtual rotation θ enARtg;snøak;mYy ehIysresrsmIkarCaGnuKmn_
eTAnwgmMuenH.
468 Appendix A

10. NPIC
Virtual displacement rbs;Fñwm mechanism RtUv)anbgðajenAkñúgrUbTI A>6 b. BIsmPaBén
kmμnþxageRkA nigkmμnþxagkñúg
⎛5 ⎞ ⎛2 ⎞
Pu (10θ ) = M pθ + M p ⎜ θ ⎟ + M p ⎜ θ ⎟
⎝3 ⎠ ⎝3 ⎠
EdleKeRbI M p CMnYseGay φb M p . edaHRsayrk Pu
Pu = 0.3333M p
RbsinebIeKminKit axial strain enAkñúgGgát; BC / sway mechanism nwgxUcRTg;RTaydUcbgðaj
enAkñúgrUbTI A>6 c CamYynwgbMlas;TItamTisedkdUcKñaRtg; B nig C . Cavi)ak muMrgVilénRKb;snøak;
TaMgGs;KWlkçN³RsedogKña³
Pu (15θ ) = M p (4θ ) b¤ Pu = 0.2667 M p
BIrUbTI A>6d/ eKalkarN_én virtual work sMrab; combined mechanism eGay
⎛5 ⎞ ⎛2 ⎞
Pu (15θ ) + Pu (10θ ) = M pθ + M p ⎜ θ ⎟ + M p ⎜ θ + θ ⎟ + M pθ
⎝3 ⎠ ⎝3 ⎠
Pu = 0.2133M p ¬lub¦
cemøIy³ Collapse load sMrab;eRKagKW Pu = 0.2133φb M p = 0.2133(1400) = 299kips
cMNaMfa vamancMnucdUcKñaxøHrvagviFIénkarviPaKTaMgBIr. eTaHbICa equilibrium method
minRtUvkarBicarNaRKb; mechanism k¾eday k¾vaRtUvkareGayeyIgdwgBI mechanism enAeBlEdlkar
EbgEcgm:Um:g;snμt;RsbeTAnwg mechanism mYy. viFITaMgBIrRtUvkarkarsnμt; failure mechanism b:uEnþ
enAkñúg equilibrium method eKRtUvRtYtBinitükarsnμt;nImYy²sMrab;suvtßiPaB nigkarEbgEckm:Um:g;Edl
GacTTYlyk)anedaysþaTic ehIyvaminRtUvkarkarGegátRKb; mechanism eT.
A >4> karKNnamuxkat; Design
dMeNIrkarénkarKNnaKWRsedogKñanwgkarviPaKEdr EtvaxusKñaRtg;faGBaØtiEdlRtUvrkCalT§
PaBm:Umg;)aøsÞicEdlRtUvkar M p . eKsÁal; collapse load EdlTTYl)anBIkarKuN service load nwgem
KuNbnÞúk.
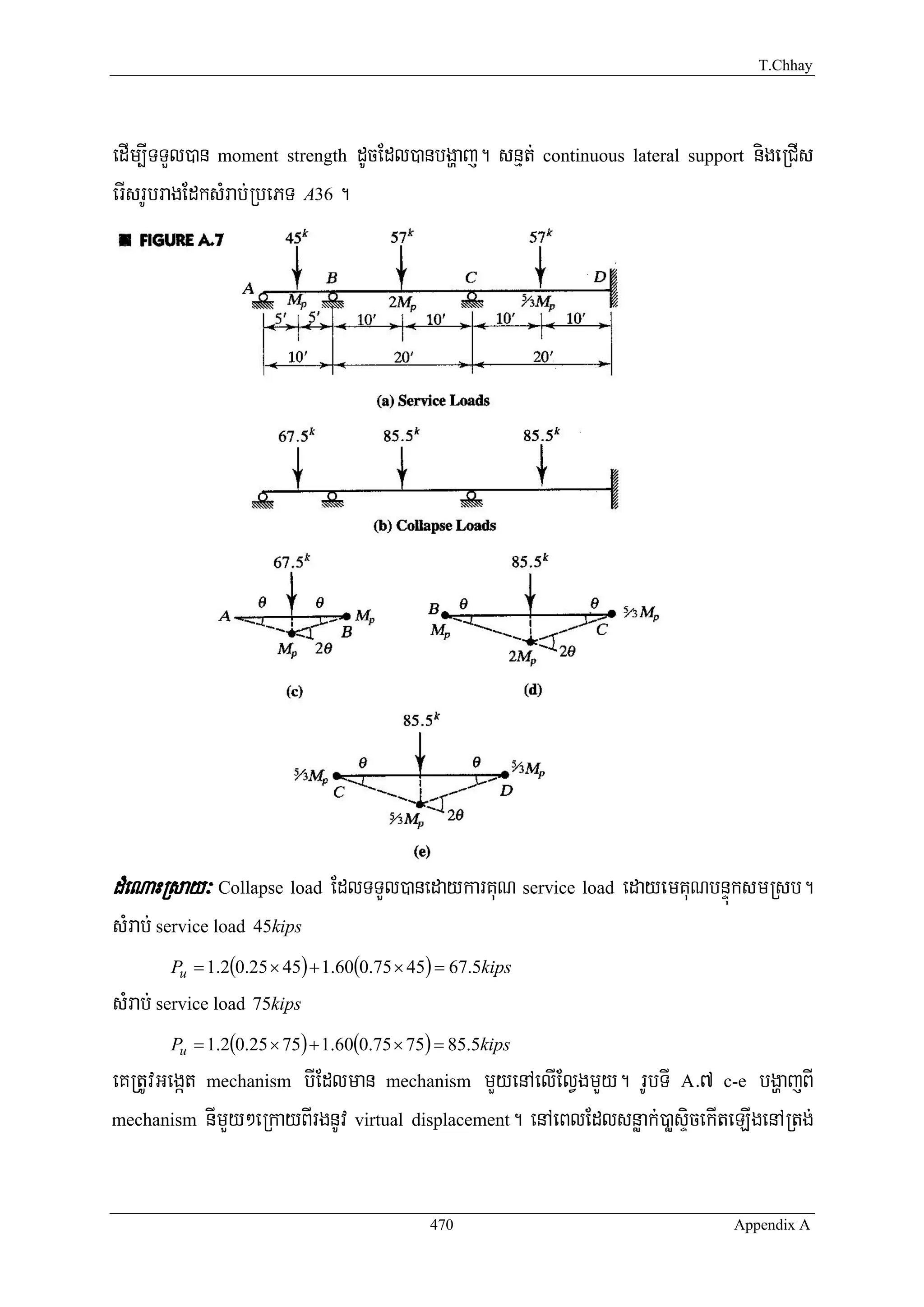
]TahrN_ A>4³ FñwmCab;bIElVgdUcbgðajenAkñúgrUbTI A>7 RtUvRTnUv gravity service load. bnÞúknI-
mYy²pSMeLIgedaybnÞúkefr 25% nigbnÞúkGefr 75% . eKeRbI cover plate enAkñúgElVg BC nig CD
469 Appendix A

11. T.Chhay
edIm,ITTYl)an moment strength dUcEdl)anbgðaj. snμt; continuous lateral support nigeRCIs
erIsrUbragEdksMrab;RbePT A36 .
dMeNaHRsay³ Collapse load EdlTTYl)anedaykarKuN service load edayemKuNbnÞúksmRsb.
sMrab; service load 45kips
Pu = 1.2(0.25 × 45) + 1.60(0.75 × 45) = 67.5kips
sMrab; service load 75kips
Pu = 1.2(0.25 × 75) + 1.60(0.75 × 75) = 85.5kips
eKRtUvGegát bIEdlman mechanism mYyenAelIElVgmYy. rUbTI A>7 c-e bgðajBI
mechanism
mechanism nImYy²eRkayBIrgnUv virtual displacement. enAeBlEdlsnøak;)aøsÞicekIteLIgenARtg;
470 Appendix A

12. NPIC
TMrEdlGgát;nImYy²minmanersIusþg;esμIKña vanwgekIteLIgenAeBlEdlm:Um:g;Bt;esμInwglT§PaBm:Um:g;)aøsÞic
rbs;Ggát;EdlexSayCag.
sMrab;ElVg AB
kmμnþxageRkA = kmμnþxagkñúg
67.5(5θ ) = M p (2θ + θ ) b¤ M p = 112.5 ft − kips
sMrab;ElVg BC
85.5(10θ ) = M pθ + 2M p (2θ ) + M pθ
5
3
b¤ M p = 128.2 ft − kips
sMrab;ElVg CD
85.5(10θ ) = M p (θ + 2θ + θ )
5
3
b¤ M p = 128.2 ft − kips
Upper-bound theorem RtUv)anbkRsaydUcxageRkam³ tMélénm:Um:g;)aøsÞicEdlRtUvKñanwg mechanism
Edlsnμt;KWtUcCag b¤esμInwgm:Um:g;)aøsÞicsMrab; collapse load. dUcenH mechanism EdlTamTarlT§PaB
m:Um:g;FMCageKCa mechanism EdlRtwmRtUv. Mechanism TaMgBIrcugeRkaymantMél M p dUcKña ehIy
GacnwgekIteLIgkñúgeBldMNalKña. CaTUeTAersIusþg;EdlRtUvkarCa design strength EdlRtUvkar dUc
enH
φb M p = 128.2 ft − kips
BI Load Factor Design Selection Table, rUbragEdlRsalCageKKW W 16 × 31 Edlman design
strength θ b M p = 146 ft − kips
sakl,g W 16 × 31 ehIyRtYtBinitükMlaMgkat; ¬eyagtamrUbTI A>8¦
sMrab;ElVg AB
∑ M B = V A (10 ) − 67.5(5) + 128.2 = 0
V A = 20.93kips
VB = 20.93 − 67.5 = −46.57 kips
sMrab;ElVg BC
⎛5⎞
∑ M B = − M p + 85.5(10) + ⎜ ⎟ M p − VC (20) = 0
⎝3⎠
85.5(10) + (2 / 3)M p 855 + (2 / 3)(128.2)
VC = = = 47.02kips
20 20
VB = 85.5 − 47.02 = 38.48kips
471 Appendix A

13. T.Chhay
sMrab;ElVg CD
∑ M C = − M p + M p + 85.5(10) − VD (20) = 0
5 5
3 3
VD = 42.75kips = VC
dUcenH kMlaMgkat;TTwgGtibrma VC KW)anmkBIElVg BC b¤esμIKña 47.02kips .
BItaragbnÞúkBRgayesμIemKuNenAkñúg Part 4 of the Manual, shear design strength rbs;
W 16 × 31 KW
φvVn = 84.9kips > 47.02kips (OK)
cemøIy³ eRbI W 16 × 31 .
A >5> karsnñidæan Conclusion Remark
karviPaKén mechanism EdlrgbnÞúkBRgaybgðajBIPaBsμúKsμajbEnßmeTotEdlmin)anerob
rab;enATIenH. bBaðaCak;EsþgenAkñúg plastic analysis or design rYmbBa©ÚlnUvkardak;bnÞúkEbbenH
y:agCak;Esþg. elIsBIenH eKKYrGegátGnþrGMeBIénT§iBlrbs;kMlaMgtamG½kS nigm:Um:g;Bt;sMrab;Ggát;
EdlrgTaMgkMlaMgtamG½kS nigm:Um:g;Bt; dUcenA rigid frame enAkñúg]TahrN_ A>4 .
cMeBaHviFIviPaKEdlmanlkçN³TUeTAdUcCa equilibrium method manniyayy:aglMGitenAkñúg
the plastic methods of structural analysis (Neal, 1977). ehIyvamanrUbmnþEdlman
lkçN³sμúKsμajsMrab; mechanism method eTotpg. CamYynwgviFIenH EdleKsÁal;faCa method of
inequalities eKGackMNt; mechanism EdlRtwmRtUveday linear programming technique eday
pÞal;. eKGaceRbI plastic design FmμtasMrab;KNnaeRKOgbgÁúMPaKeRcIn b:uEnþCaTUeTA mechanism
method EdlbgðajenAkñúg]bsm<½n§enHKWRKb;RKan;ehIy.
472 Appendix A