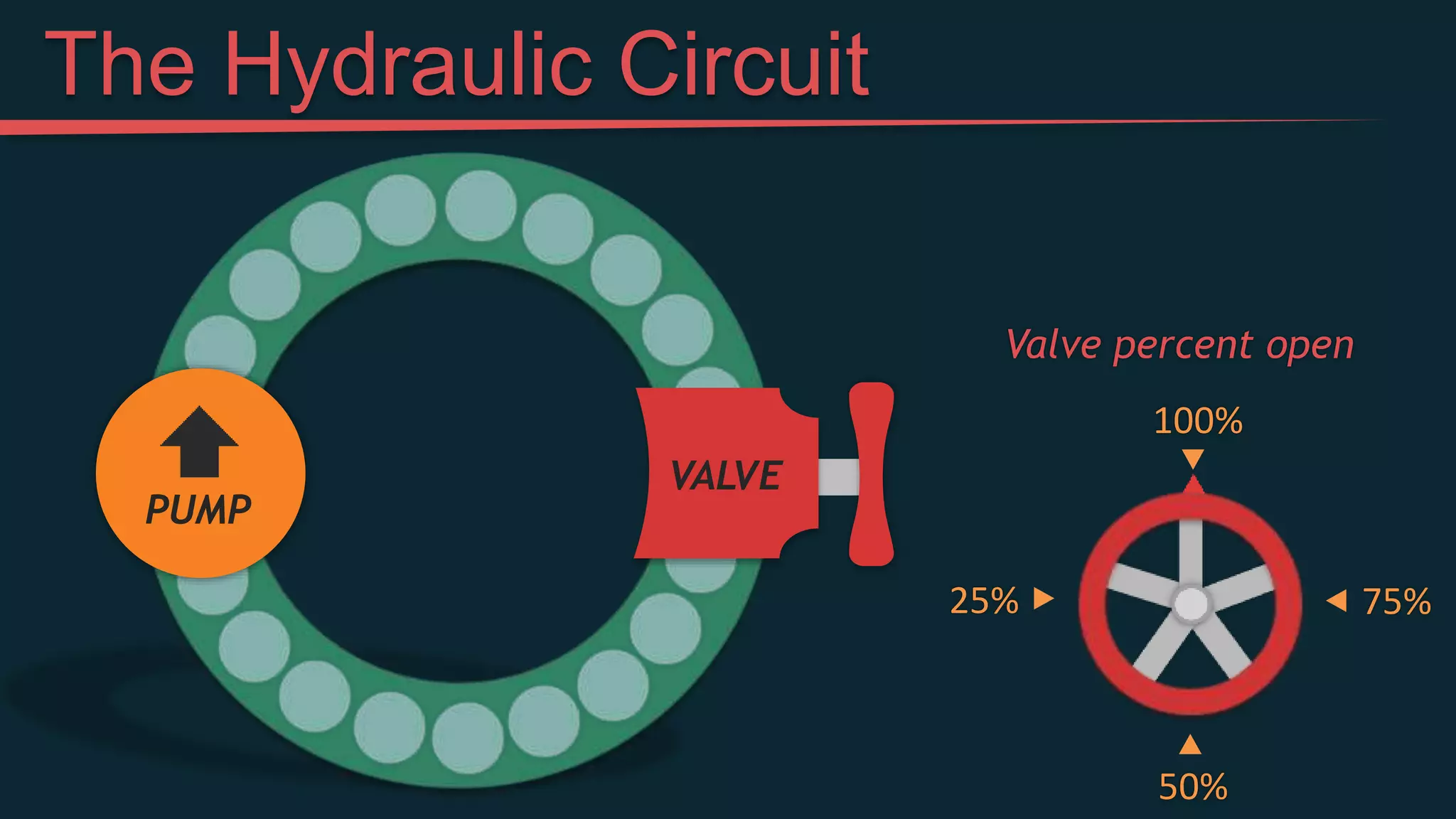
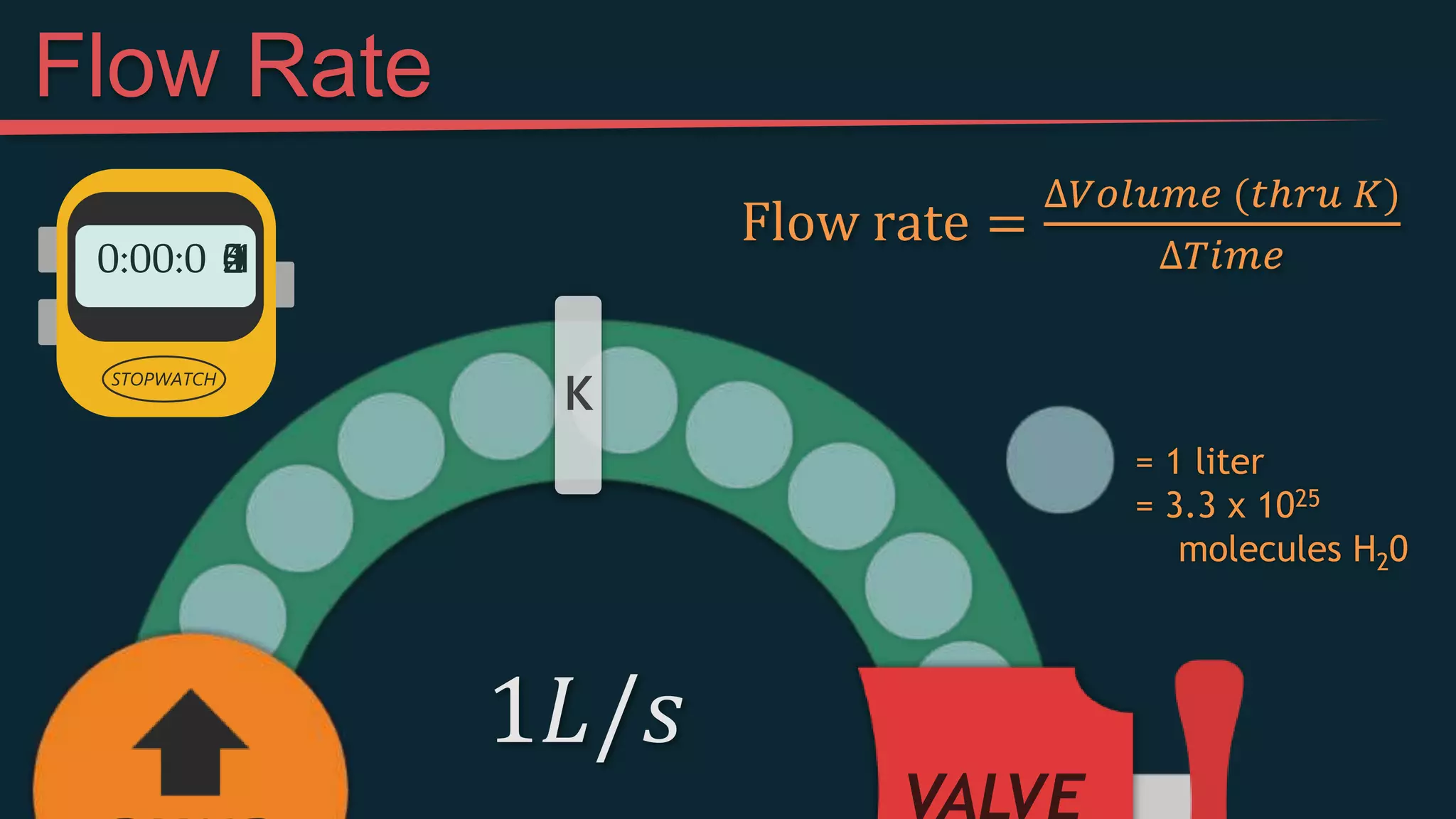
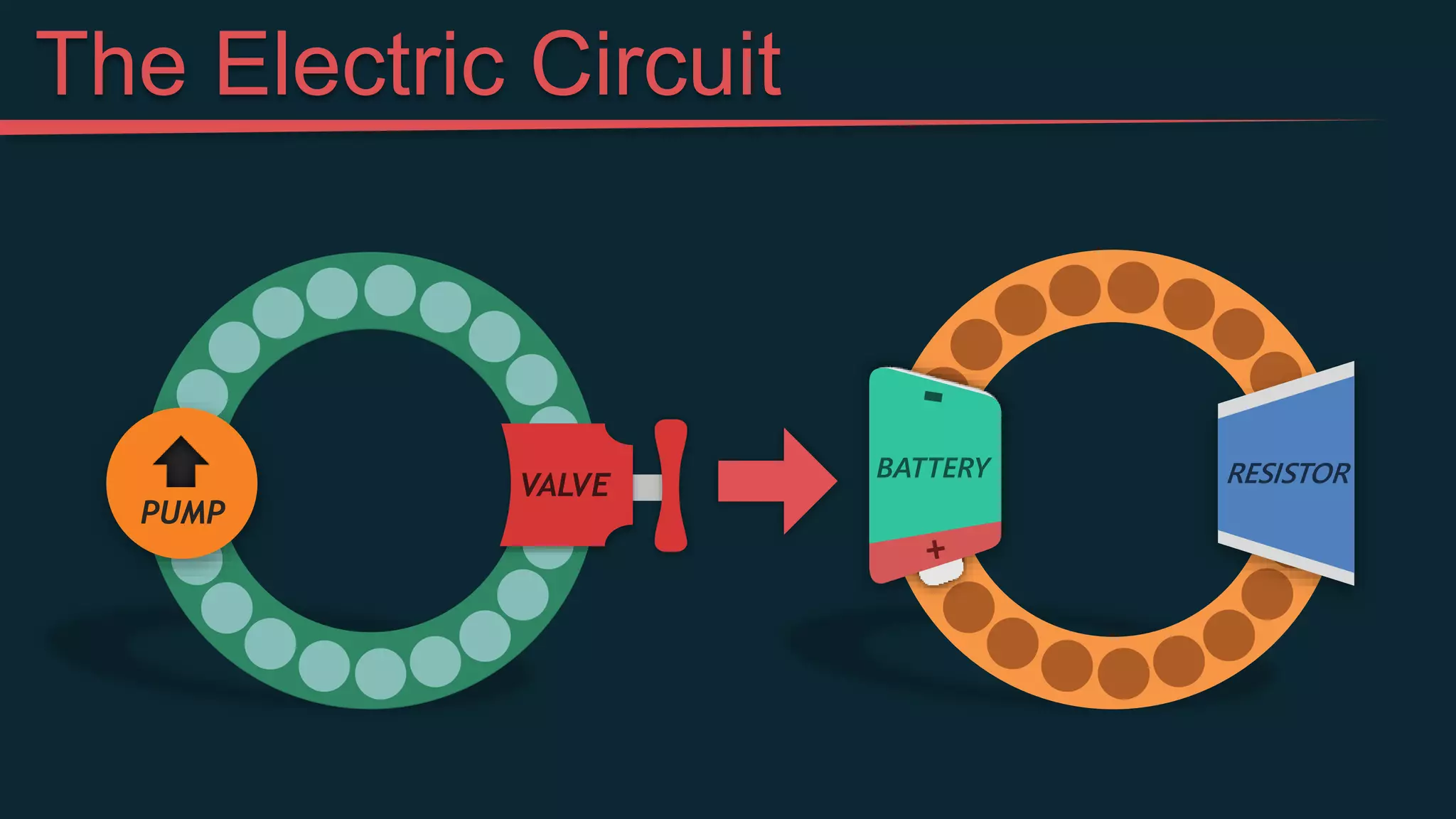
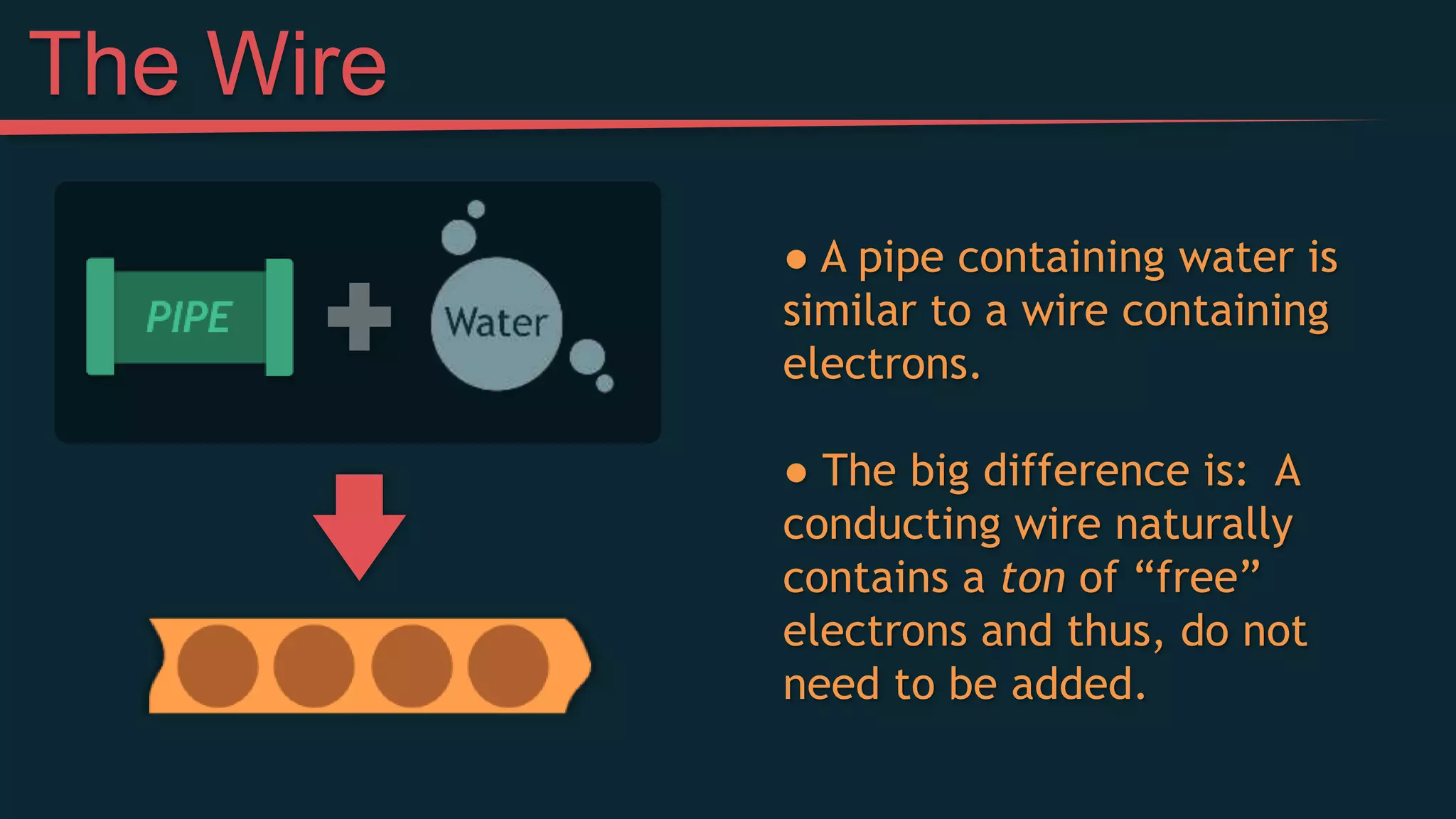
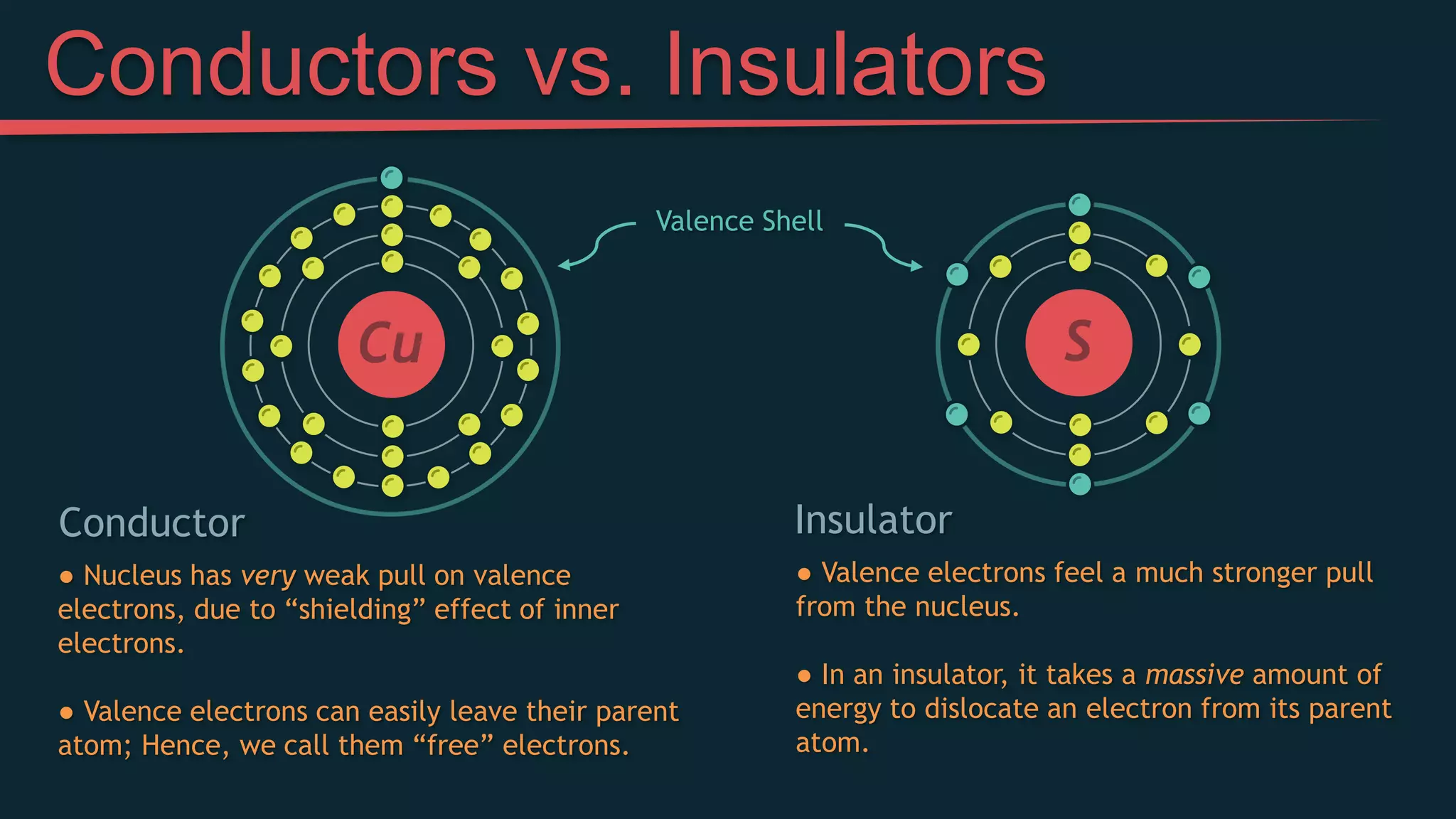
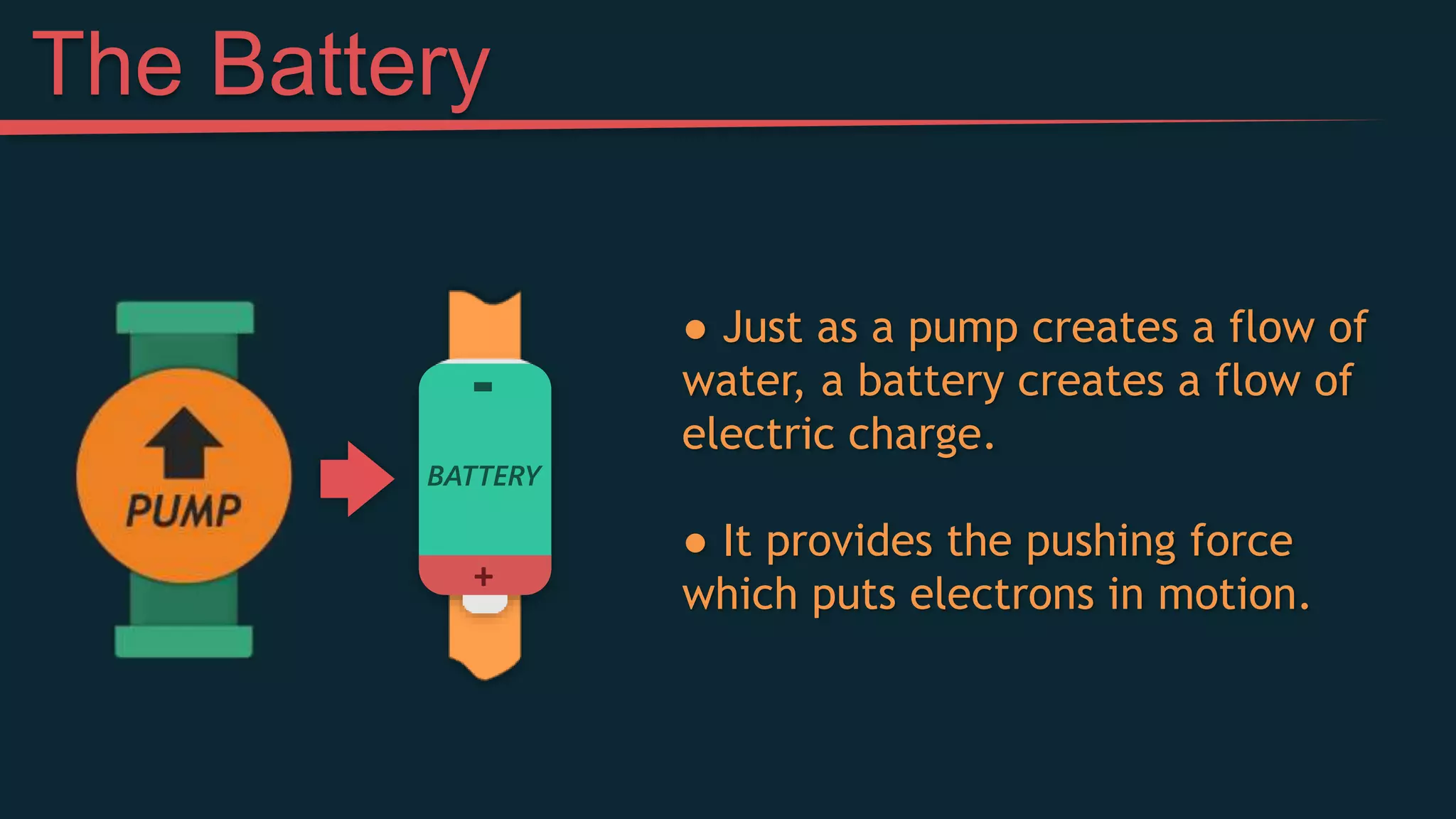
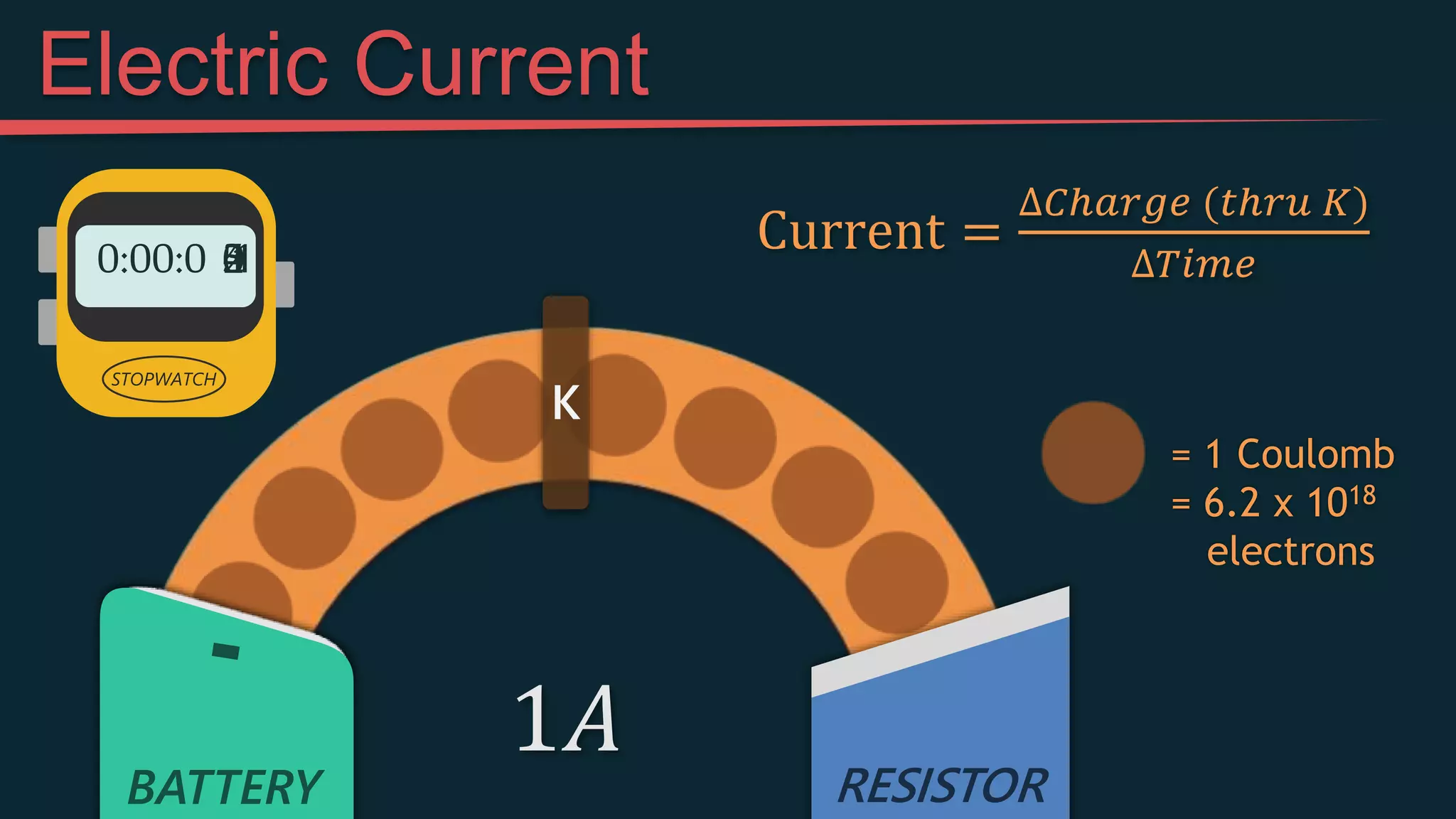
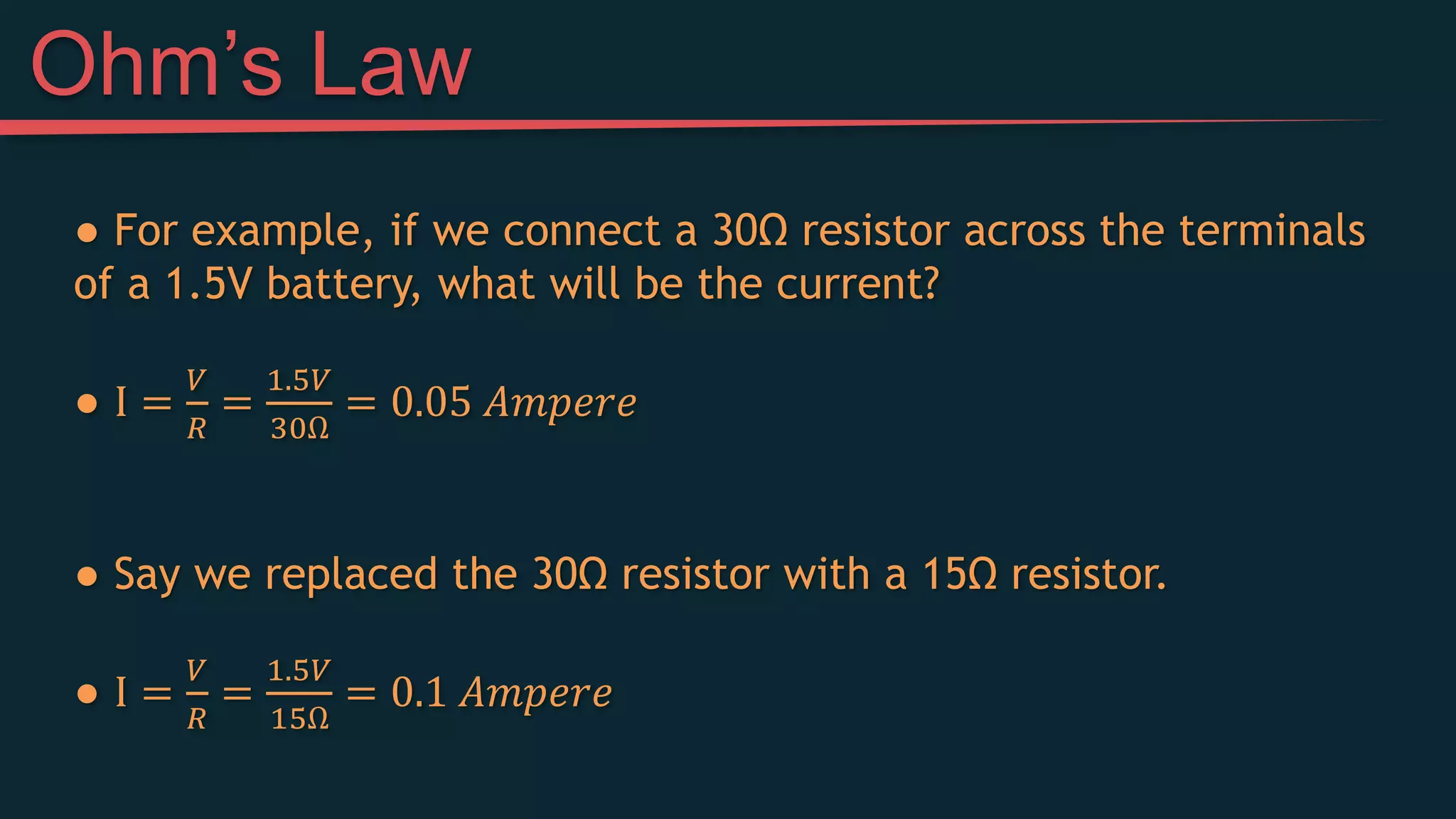
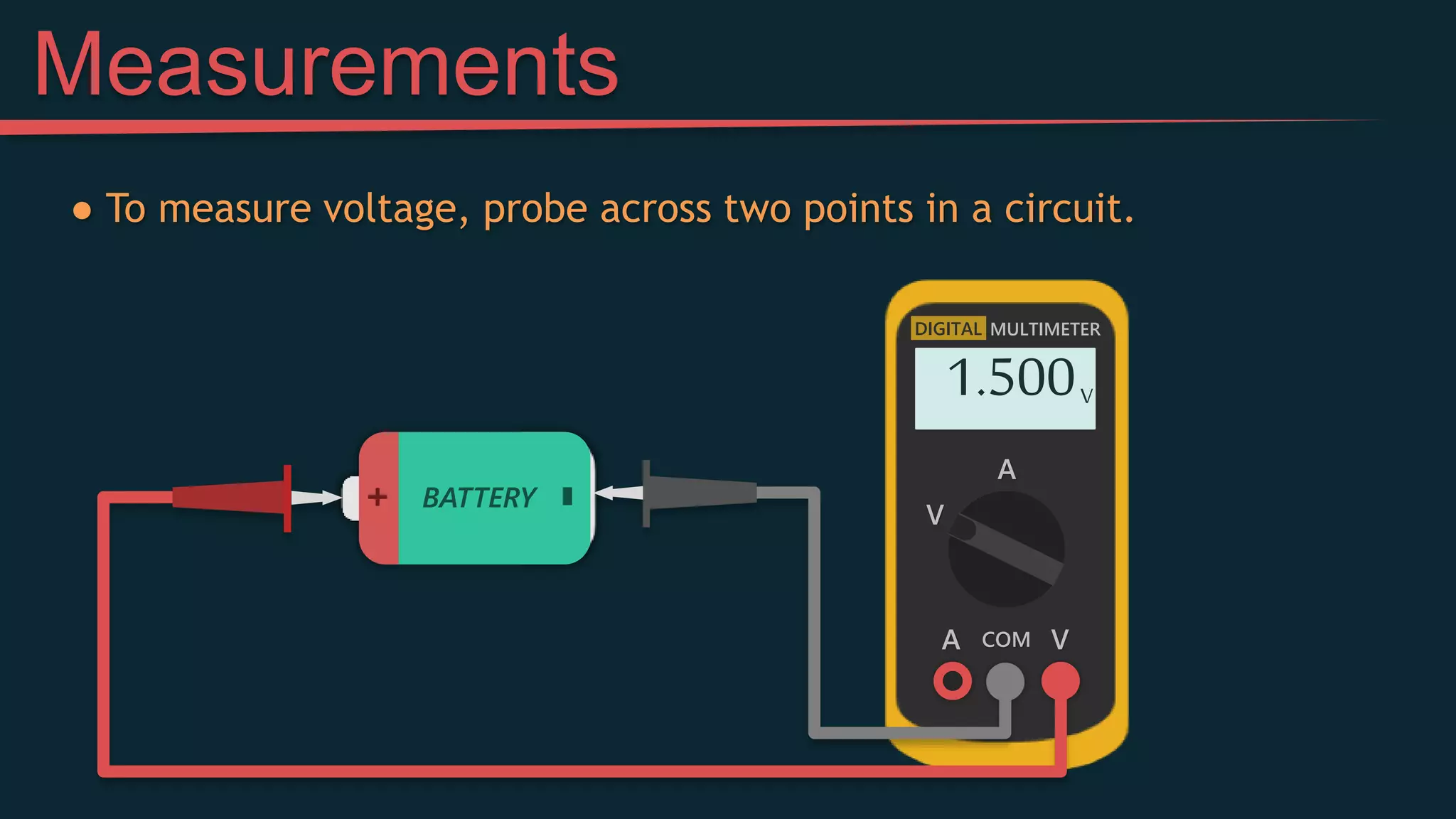
This document provides an introduction to simple electric circuits through an analogy to hydraulic circuits. It compares water flowing through pipes to electrons flowing through wires, with pumps supplying pressure, valves controlling flow, and resistors impeding flow. Key circuit elements like batteries, which provide voltage to push electrons, and resistors, which limit current, are explained. Ohm's Law, which relates voltage, current, and resistance, is derived. The document concludes by discussing measuring voltage and current in a circuit using a multimeter.

1. By Solid State Workshop
An introduction to
Simple Electric Circuits
3rd Edition

2. Objectives
In this video, we will…
1. Walk through an analogy
2. Compare the analogy to an electric circuit
3. Discuss the underlying physics (high-level view)
4. Introduce a fundamental equation (easy!)
5. Relate new circuit knowledge to the real world
6. Learn how to make measurements in the lab

3. VALVE
PUMP
100%
50%
75%
25%
Valve percent open
The Hydraulic Circuit

4. = 1 liter
= 3.3 x 1025
molecules H20
Flow rate =
∆𝑉𝑜𝑙𝑢𝑚𝑒 (𝑡ℎ𝑟𝑢 𝐾)
∆𝑇𝑖𝑚𝑒
K
Flow Rate
STOPWATCH
0:00:0 0
1
2
3
4
5
1𝐿/𝑠

5. PIPE
● The piping contains the water.
Wherever the piping goes, the
water flows.
● For the sake of this analogy, we
assume the pipe does not hinder
the flow of water.
The Piping

6. Water
● Water is the substance that
flows through the circuit.
● The flow of water allows us
to do useful work.
Water

7. ● The pump gives water kinetic
energy and accelerates it through
the circuit.
● Flow rate can be modified by
adjusting the applied power, or by
selecting a different size pump.
PUMP
Power
Regulator
The Pump

8. VALVE
● The valve limits the rate of
flow of water.
● If the pump power is held
constant, the flow rate depends
entirely on the valve.
The Valve

9. ● All matter is composed of tiny, fundamental particles.
● The charge of a particle determines how it will act in the
presence of another charged particle.
● Particles of the same “sign” repel, while opposites attract.
+ -
Electric Charge
- -

10. ● Electric circuits deal with electrons,
the negatively charged particles which
orbit an atom’s nucleus.
● The unit of charge is the Coulomb (C).
● You need 6.2 x 1018 electrons to make
1 Coulomb of charge.
● A Coulomb’s worth of electrons is like
a liter’s worth of water molecules.
Electric Charge

11. VALVE
PUMP
RESISTOR
BATTERY
The Electric Circuit

12. ● A pipe containing water is
similar to a wire containing
electrons.
● The big difference is: A
conducting wire naturally
contains a ton of “free”
electrons and thus, do not
need to be added.
The Wire

13. Conductors vs. Insulators
● Nucleus has very weak pull on valence
electrons, due to “shielding” effect of inner
electrons.
● Valence electrons can easily leave their parent
atom; Hence, we call them “free” electrons.
S
● Valence electrons feel a much stronger pull
from the nucleus.
● In an insulator, it takes a massive amount of
energy to dislocate an electron from its parent
atom.
Conductor Insulator
Cu
Valence Shell

14. ● Just as a pump creates a flow of
water, a battery creates a flow of
electric charge.
● It provides the pushing force
which puts electrons in motion.
-
The Battery
BATTERY
+
-

15. The Battery
Battery - Battery +
External Circuit
● Imagine a tube completely filled with marbles.
● Adding one marble to the tube causes the entire line of
marbles to shift by one unit, resulting in the loss of one marble
at the opposite end.

16. ● The pushing force “felt”
by electrons in a wire is due
to a difference in electric
potential between the two
terminals of a battery.
Potential Difference
Tendency to Gain Electrons
+
Positive terminal
wants to gain
electrons
- Negative terminal
wants to give away
electrons
Potential
Difference

17. ● The unit of potential difference is the volt (V).
● More potential difference means more pushing
force applied to free electrons.
● Potential difference is an across-variable,
meaning it is measured across a device, or
between two points.
1.5V BATTERY
-
+
Potential Difference
Alkaline
battery

18. ● Just as a valve limits the rate
of flow of water, a resistor limits
the rate of flow of electrons.
● Without a resistor, the flow of
charge is essentially unbounded.
(i.e. smoke and flames)
RESISTOR
The Resistor

19. Resistance
RES
● A resistor is really just a poor conductor.
● It allows the flow of electrons, just not
particularly well.
● Resistance describes how much a resistor
“pushes back” against the flow of charge.
● The unit of resistance is the ohm (Ω).

20. ● Electric current has the unit Ampere (A)
and quantifies the rate of flow of charge.
● 1𝐴𝑚𝑝𝑒𝑟𝑒 = 1 𝐶𝑜𝑢𝑙𝑜𝑚𝑏
1 𝑠𝑒𝑐𝑜𝑛𝑑
● Current is a through-variable which
describes the quantity of charge which flows
through a surface in some amount of time.
Electric Current
Electrons flowing
through a cross-section
of copper wire
ELECTRON
COUNTER
0 0 2 7
● A flow of charge is called an electric current.

21. K
Current =
∆𝐶ℎ𝑎𝑟𝑔𝑒 (𝑡ℎ𝑟𝑢 𝐾)
∆𝑇𝑖𝑚𝑒
= 1 Coulomb
= 6.2 x 1018
electrons
BATTERY RESISTOR
Electric Current
STOPWATCH
0:00:0 0
1
2
3
4
5
1𝐴

22. ● There is a simple relationship we can use to relate voltage,
resistance, and current. It is called Ohm’s Law.
● 𝐶𝑢𝑟𝑟𝑒𝑛𝑡 (𝐼) =
𝑃𝑜𝑡𝑒𝑛𝑡𝑖𝑎𝑙 𝐷𝑖𝑓𝑓𝑒𝑟𝑒𝑛𝑐𝑒 (𝑉)
𝑅𝑒𝑠𝑖𝑠𝑡𝑎𝑛𝑐𝑒 (𝑅)
● 𝐼 =
𝑉
𝑅
or 𝑅 =
𝑉
𝐼
or 𝑉 = 𝐼 ∙ 𝑅
● This equation can be rearranged to solve for any unknown element.
Ohm’s Law
Note that the letter “I ” is
used to denote current.

23. ● For example, if we connect a 30Ω resistor across the terminals
of a 1.5V battery, what will be the current?
● I =
𝑉
𝑅
=
1.5𝑉
30Ω
= 0.05 𝐴𝑚𝑝𝑒𝑟𝑒
● Say we replaced the 30Ω resistor with a 15Ω resistor.
● I =
𝑉
𝑅
=
1.5𝑉
15Ω
= 0.1 𝐴𝑚𝑝𝑒𝑟𝑒
Ohm’s Law

24. ● In a similar manner, if we know the current and the voltage,
we can determine the value of an unknown resistor.
● Suppose we have a 12V battery and measure a current of
0.04A through the resistor. What must be the value of the
resistor?
● 𝑅 =
𝑉
𝐼
=
12𝑉
0.04𝐴
= 300Ω
Ohm’s Law

25. Resistors…What’s the Point?
● Resistors are all about control!
● In electronics, resistors are used to precisely
control currents and voltages at many points
in a circuit.
● For example, a transistor can be configured
as an amplifier by careful selection and
arrangement of surrounding resistors. Examples of resistors commonly
found in electronics

26. Electrical Loads
● We generally think of resistors as the
little devices shown in the previous slide.
● However, anything which draws a
certain amount of current, given some
input voltage, can be modeled as a
resistor.
● We call these things electrical loads.
Some useful
electrical loads

27. V
A COM
MULTIMETER
1.500
DIGITAL
V
A
● To measure voltage, probe across two points in a circuit.
BATTERY
-
+
Measurements
V

28. V
A COM
MULTIMETER
0.050
DIGITAL
V
A
● To measure current, you must redirect all of the current you want to measure
through the meter. Therefore, break the circuit and insert the meter “in series”
with the circuit.
Measurements
30Ω
A
1.5V
BATTERY
-
+
Remember to
switch to “A”
input jack!

29. Thanks for watching!
I’d love to hear your feedback!
Subscribe