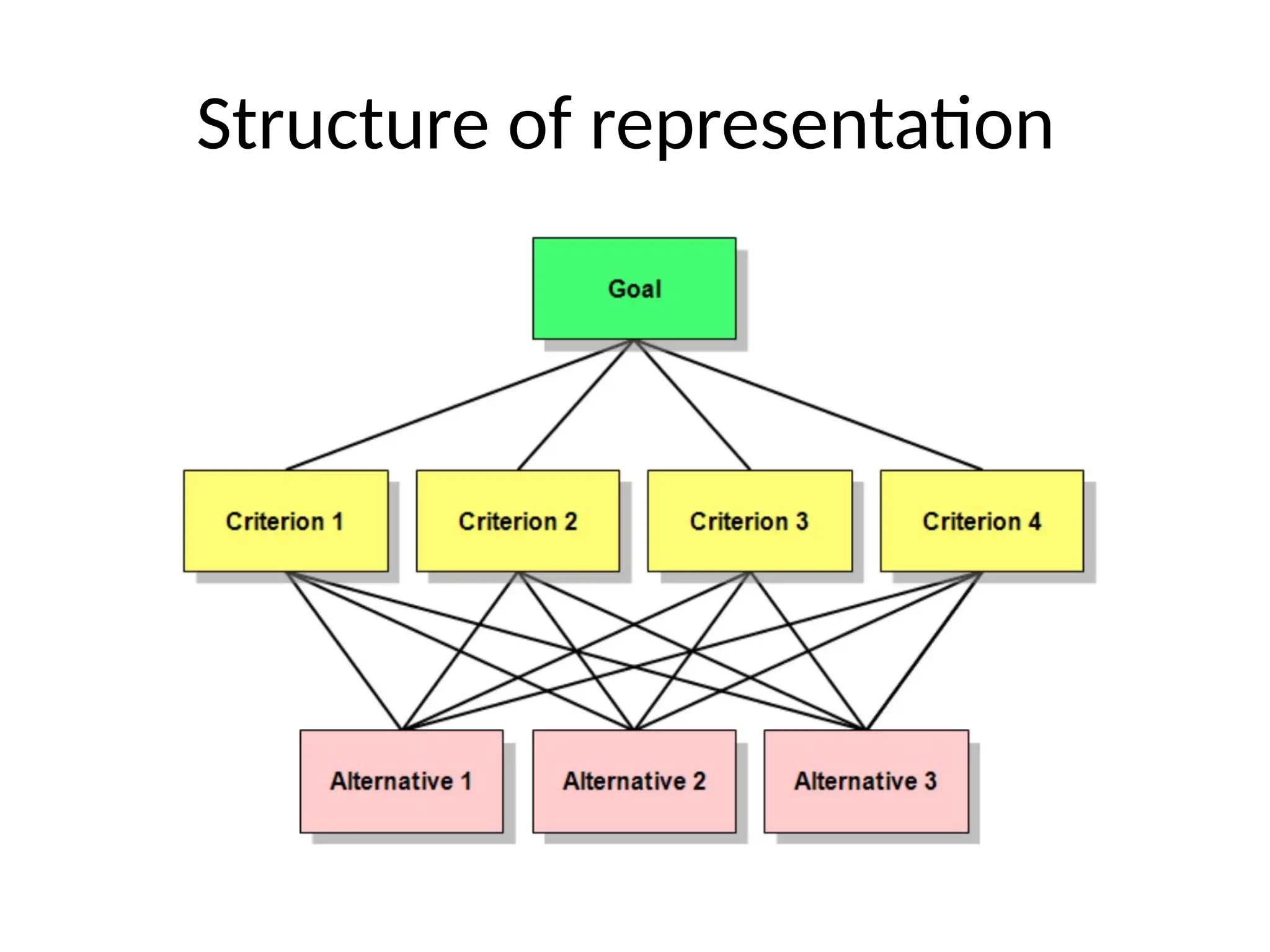
The Analytic Hierarchy Process (AHP) is a multi-criteria decision-making method that structures complex decisions hierarchically and quantifies managerial judgments of conflicting criteria. It involves steps such as creating a pairwise comparison matrix and calculating consistency ratios to derive a priority vector for decision alternatives. AHP has strengths like flexibility and support for group decision-making, but it also has weaknesses including potential ranking irregularities and the need for numerous pairwise comparisons.

1. Analytic Hierarchy Process

2. Introduction
• The Analytic Hierarchy Process is a powerful and flexible multi criteria
decision making method that can be applicable in variety of decision making
situation from simple to complex situation.
• It is specially used to quantify managerial judgment of the relative importance
of each of several conflicting criteria used in decision making process.
• In this method a problem is put into a hierarchical structure.
• The structure are
a) The overall objective of the decision.
b) Factors or criteria for the decision.
c) Sub factors under those factors.
d) Decision option.

3. Structure of representation

4. The steps involved in AHP model
• Step-1: List the overall goal, criteria and decision alternatives.
• Step-2: Develop a pair wise comparison matrix. Rate the
relative importance between each pair of decision
alternatives and this rate is based on Saaty‘s nine point scale.
The matrix lists the alternatives horizontally and vertically and
has the numerical rating comparing the horizontal (first)
alternative with the vertical (second) alternative.

5. • Step-3: Develop a normalized matrix by dividing each number in
a column in the pair wise comparison matrix by its column sum.
• Step-4: Develop a priority vector. Average each row of the
normalized matrix. The row average forms the priority vector of
alternative preferences with respect to the particular criterion.
• Step-5: Calculate the Consistency Ratio [CR]. Calculate the
eigenvector or the relative weights and for each matrix of order
n. Compute consistency index using CI=(λmax−n)/(n−1), RI=
Random Inconsistency = 1.987(n-2)/n and CR= CI/RI.
• Step-6: Develop the overall priority vector by multiplying
normalized matrix of criteria with the priority matrix of decision
alternatives which is formed with priority vectors of different
criteria. With this priority values judgment is been taken care.

6. Strengths and weaknesses
• Strengths:
1. The advantages of AHP over other multi criteria methods are its
flexibility, intuitive appeal to the decision makers and its ability to
check inconsistencies. Generally, users find the pairwise
comparison form of data input straightforward and convenient..
2. Additionally, the AHP method has the distinct advantage that it
decomposes a decision problem into its constituent parts and
builds hierarchies of criteria.
3. AHP helps to capture both subjective and objective evaluation
measures.
4. The AHP method supports group decision.
5. AHP is uniquely positioned to help model situations of
uncertainty and risk since it is capable of deriving scales where
measures ordinarily do not exist

7. • Weaknesses:
1. Many researchers have long observed some cases in which ranking
irregularities can occur when the AHP or some of its variants are
used. This rank reversal is likely to occur e.g. when a copy or a near
copy of an existing option is added to the set of alternatives that
are being evaluated.
2. The AHP−method can be considered as a complete aggregation
method of the additive type. The problem with such aggregation is
that compensation between good scores on some criteria and bad
scores on other criteria can occur.
3. With AHP the decision problem is decomposed into a number of
subsystems, within which and between which a substantial number
of pairwise comparisons need to be completed. This approach has
the disadvantage that the number of pairwise comparisons to be
made