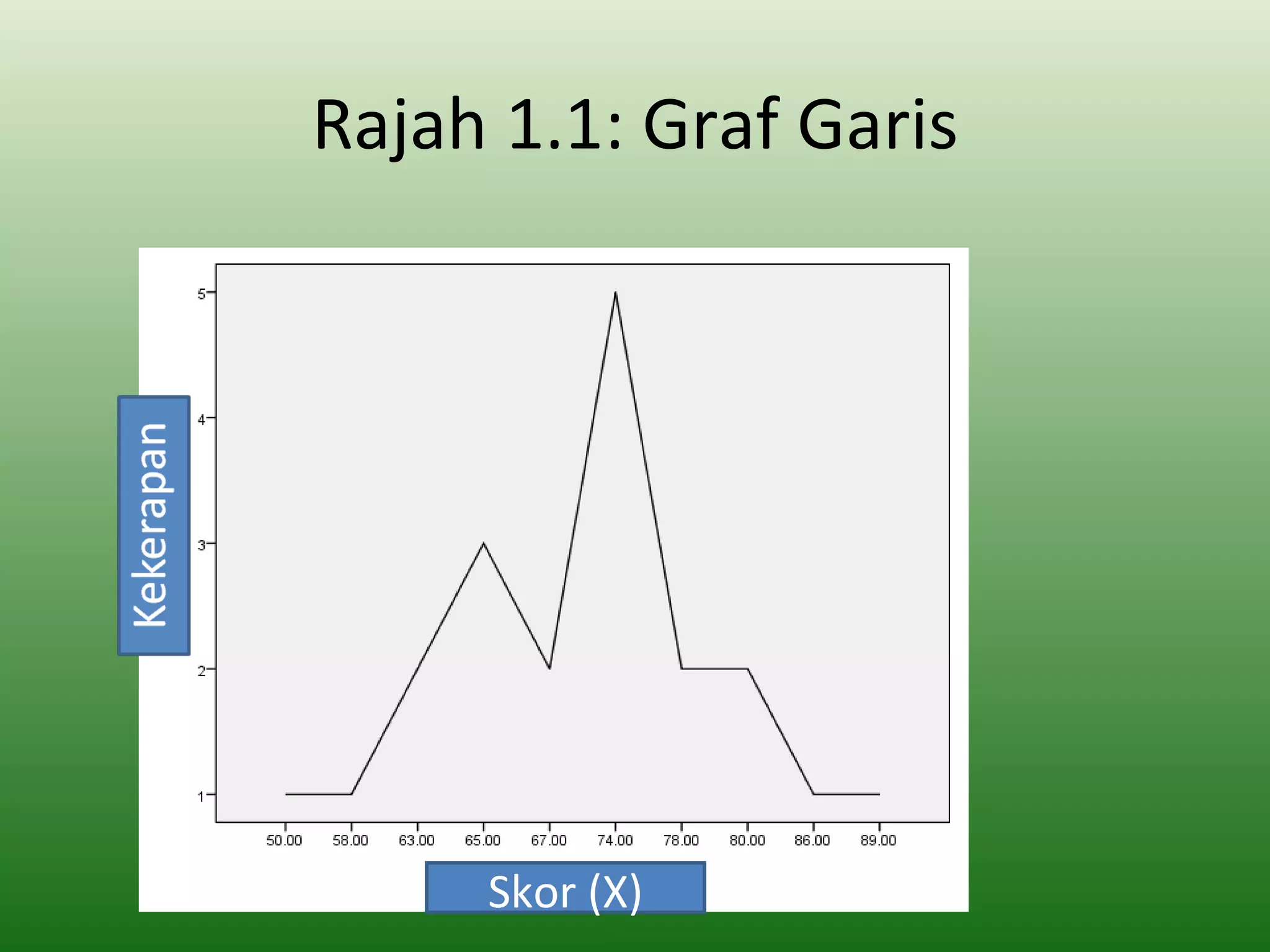
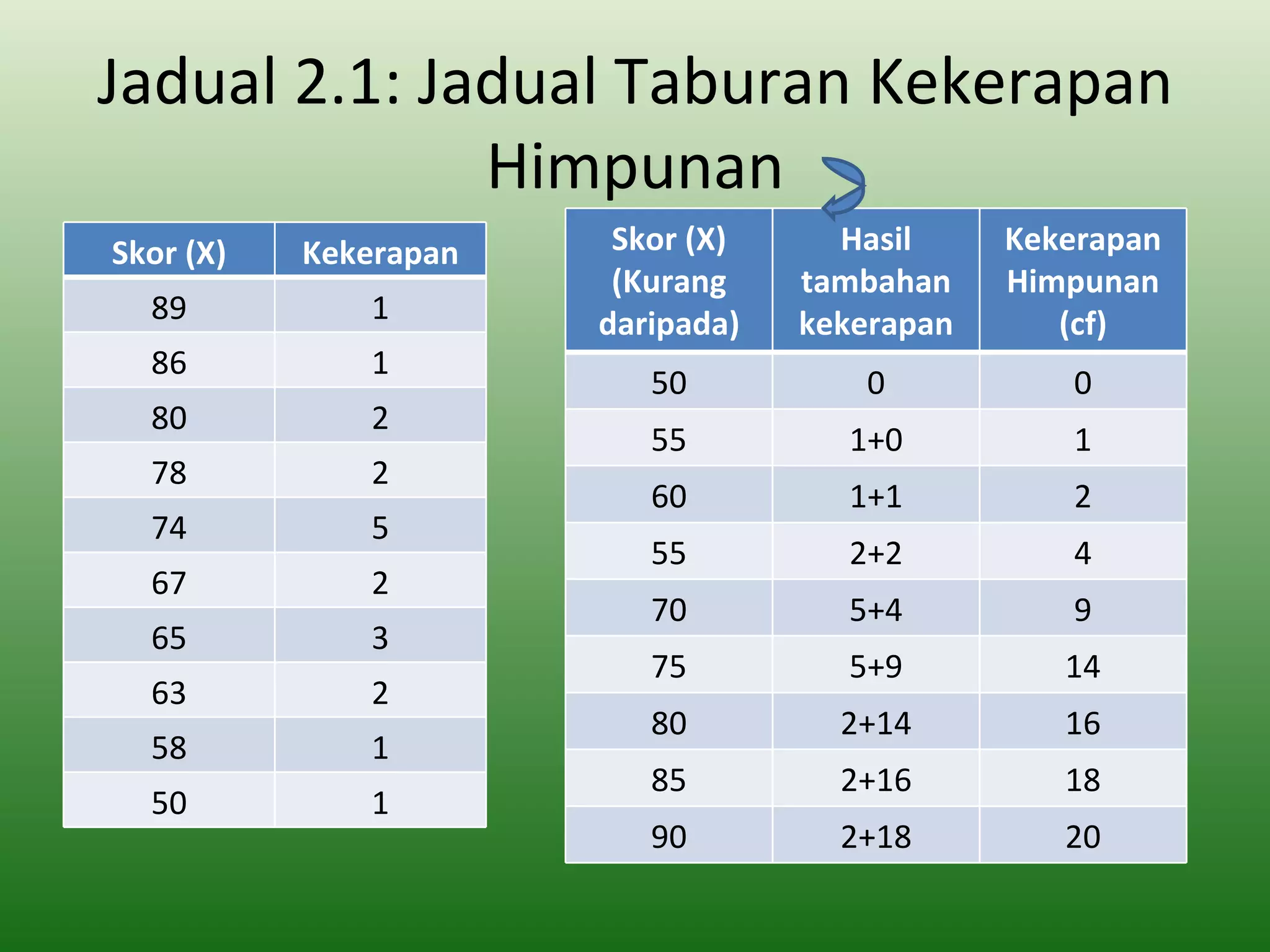
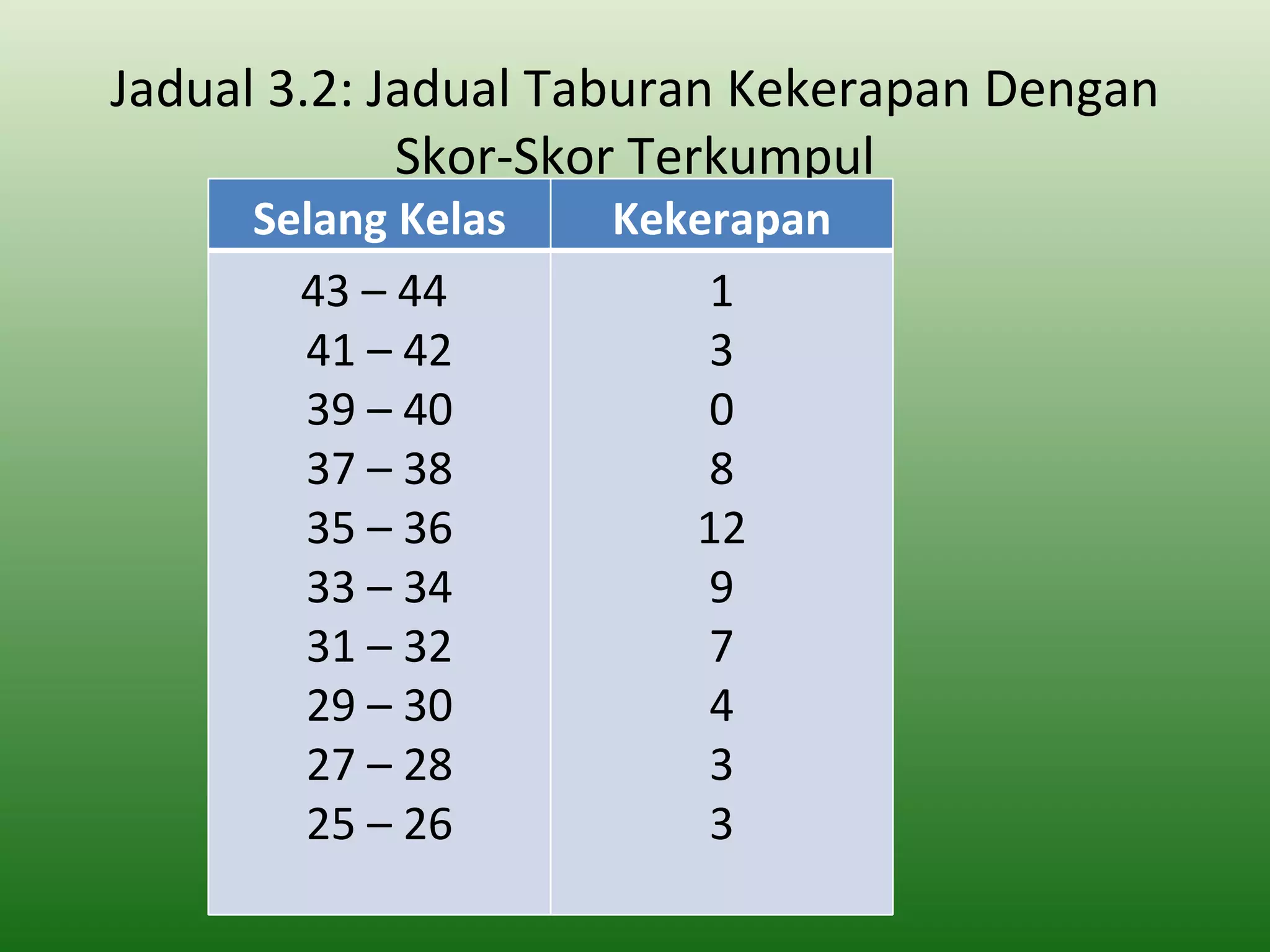
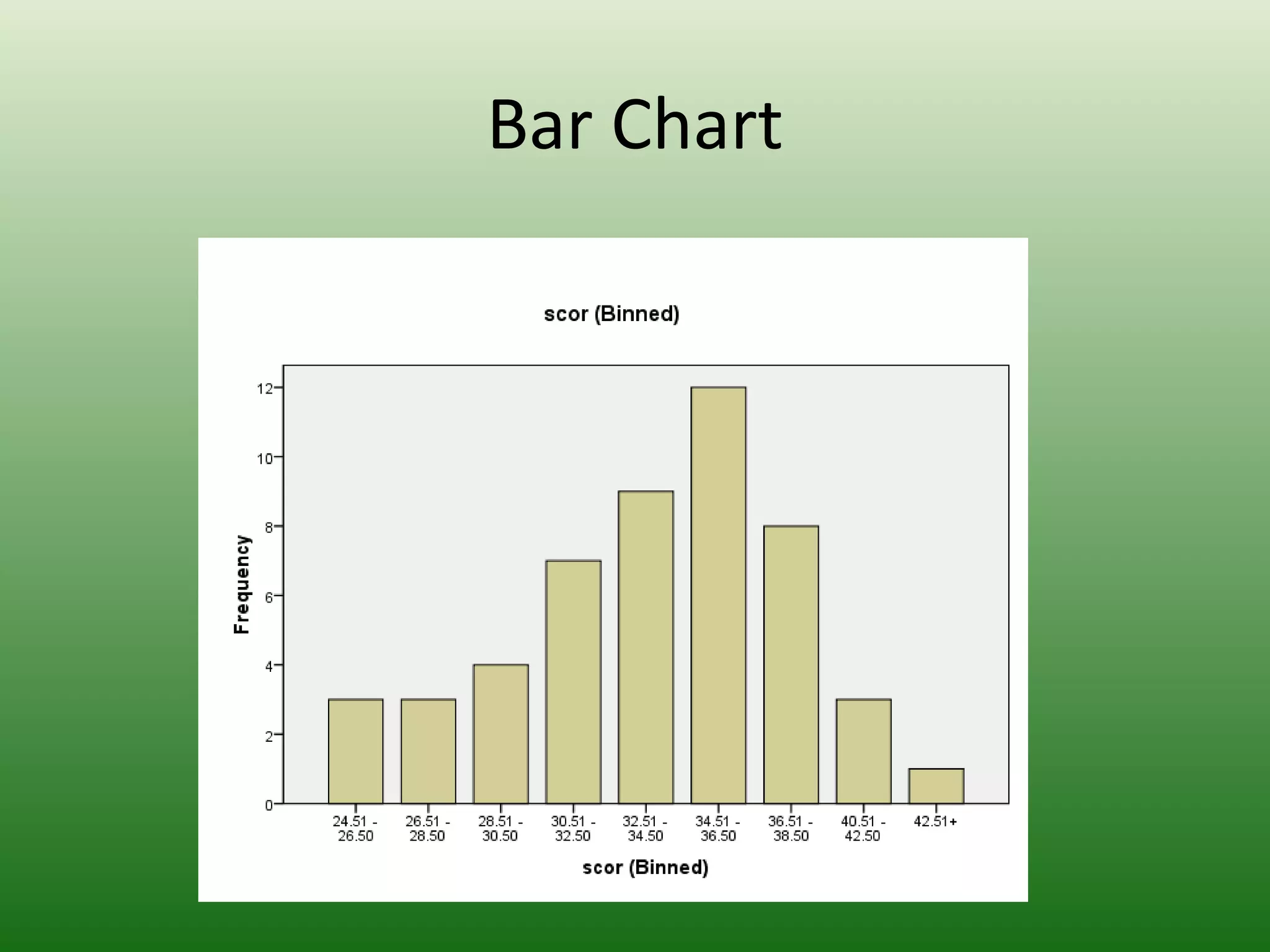
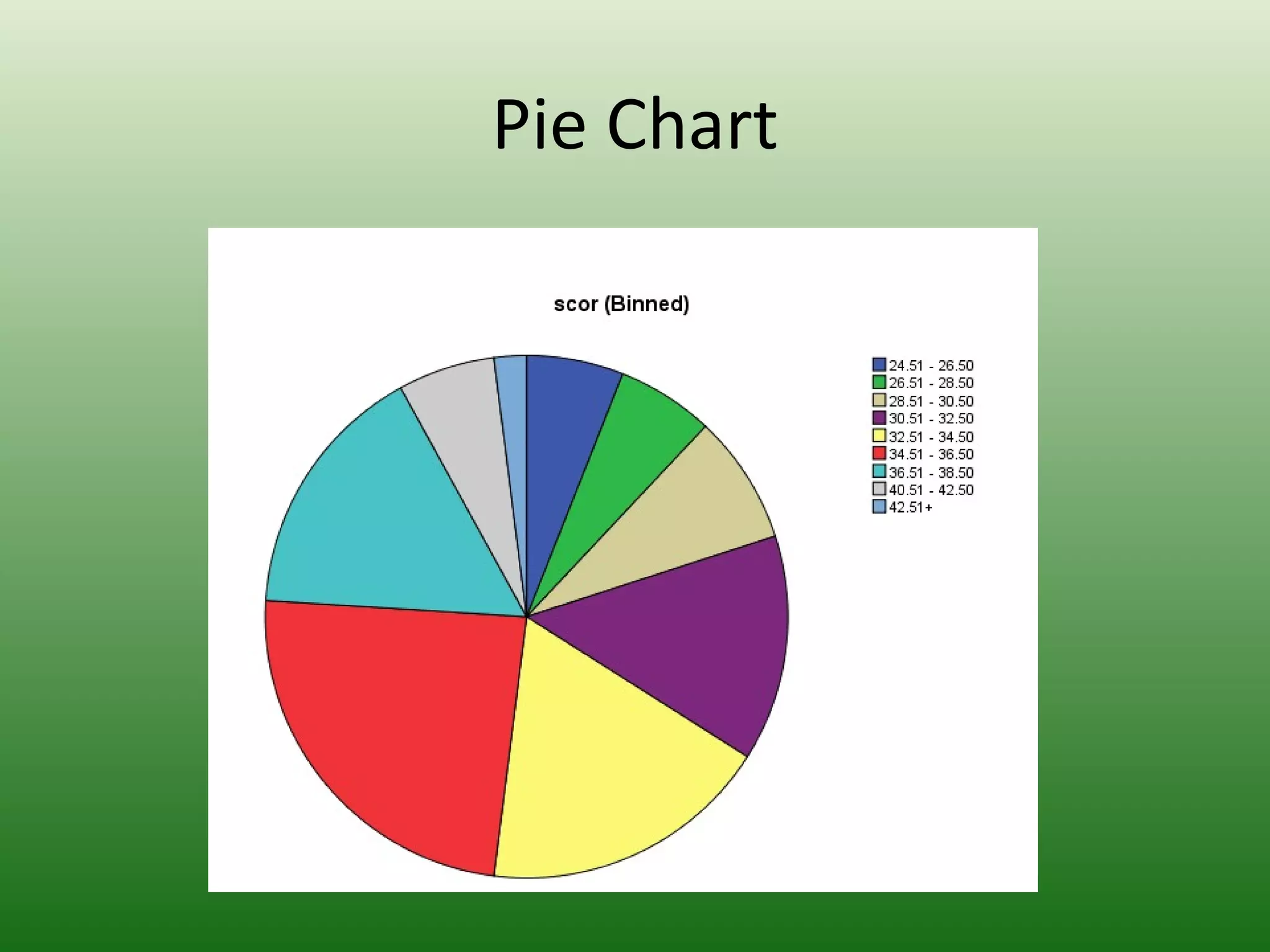
Dokumen ini membincangkan analisis dan pentafsiran data ujian yang melibatkan penggunaan perangkaan untuk mengumpul dan menyusun skor ujian. Ia menerangkan cara memindahkan skor mentah ke dalam jadual taburan kekerapan dan mengira ukuran kecenderungan memusat seperti min, median, dan mod. Ini bertujuan untuk memudahkan penganalisaan dan tafsiran dalam proses penilaian di peringkat sekolah.