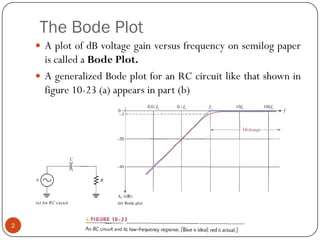
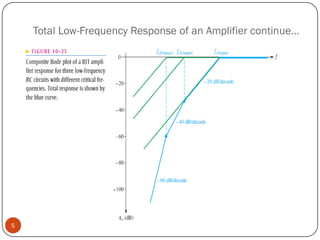
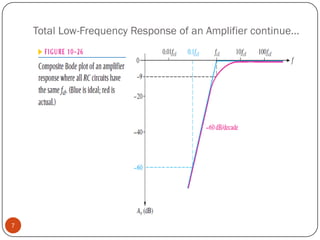
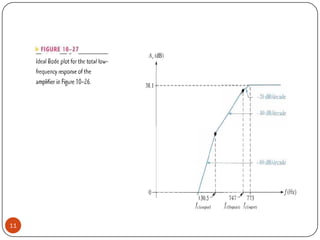
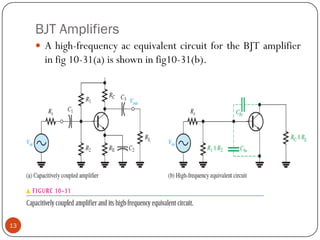
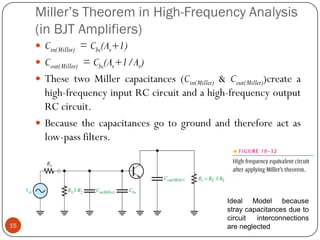
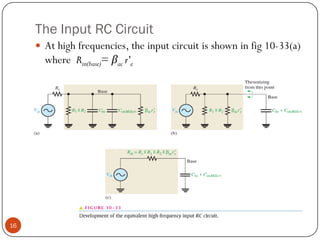
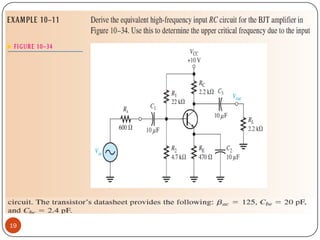
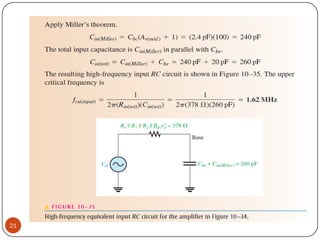
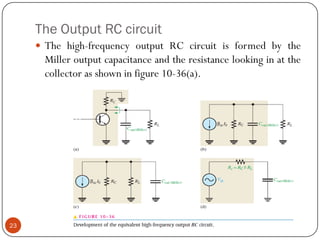
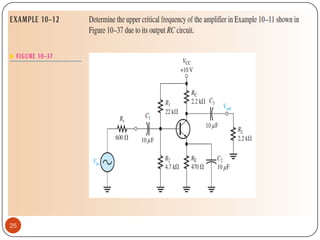
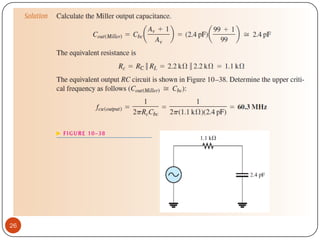
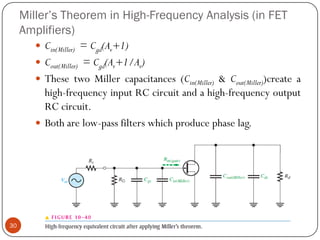
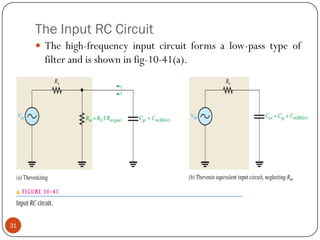
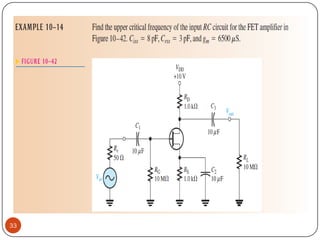
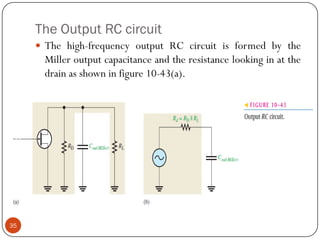
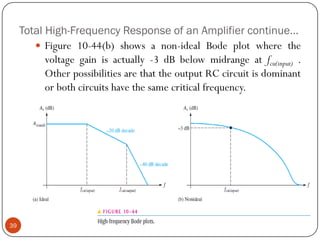
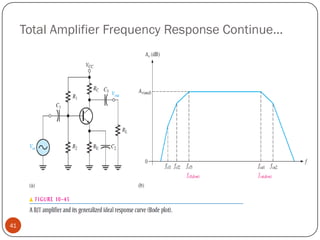
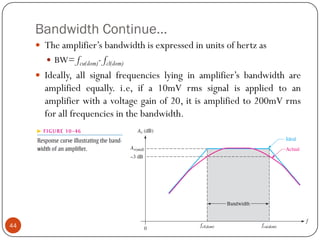
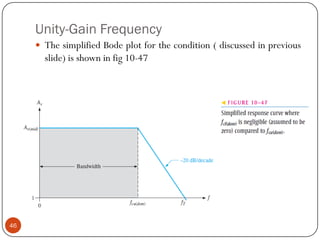
This document discusses the frequency response of amplifiers. It explains that an amplifier's frequency response can be analyzed using a Bode plot. An amplifier's bandwidth is defined as the range of frequencies between its lower and upper critical frequencies (fcl(dom) and fcu(dom)), where the voltage gain is 3dB below the midrange value. The unity-bandwidth product states that for an amplifier with a -20dB/decade roll-off, the product of its voltage gain and bandwidth remains constant. The unity-gain frequency, fT, is the frequency at which the amplifier's gain reaches 1, and it is always equal to the midrange voltage gain multiplied by the bandwidth. When analyzing multistage ampl

1. Engr.Tehseen Ahsan
Lecturer, Electrical Engineering Department
EE-307 Electronic Systems Design
HITEC University Taxila Cantt, Pakistan
Amplifier Frequency Response (Part 2)

2. The Bode Plot
AplotofdBvoltagegainversusfrequencyonsemilogpaperiscalledaBodePlot.
AgeneralizedBodeplotforanRCcircuitlikethatshowninfigure10-23(a)appearsinpart(b)
2

3. The Bode Plot continue…
Theidealresponsecurveisshowninblue.Noticethatitisflat(0dB)downtocriticalfrequencyatwhichpointthegaindropsat-20dB/decade.
Abovefcarethemidrangefrequencies.Theactualresponsecurveisshowninred.
Theactualresponsecurvedecreasesgraduallyinmidrangeandisdownto-3dBatthecriticalfrequency.
Often,theidealresponseisusedtosimplifyamplifieranalysis
Thecriticalfrequencyatwhichthecurvebreaksintoa-20dB/decadedropissometimescalledthelowerbreakfrequency.
3

4. Total Low-Frequency Response of an Amplifier
Let’slookatthecombinedeffectofthethreeHigh-passRCcircuitsinaBJTamplifier.
EachcircuithasacriticalfrequencydeterminedbyRandCvalues.
ThecriticalfrequenciesofthethreeRCcircuitsarenotnecessarilyallequal.
IfoneoftheRCcircuitshasacritical(break)frequencyhigherthantheothertwothenitisthedominantRCcircuit.
Thedominantcircuitdeterminesthefrequencyatwhichtheoverallgainofamplifierbeginstodropat-20dB/decade.
Theothercircuitseachcauseanadditional-20dB/decaderoll-offbelowtheirrespectivecritical(break)frequencies. 4

5. Total Low-Frequency Response of an Amplifier continue… 5

6. Total Low-Frequency Response of an Amplifier continue…
RefertoBodeplotinfigure10-25whichshowsthesuperimposedidealresponsesforthreeRCcircuits(greenLines)ofaBJTamplifier.
EachRCcircuithasadifferentcriticalfrequency.
TheinputRCcircuitisdominant(highestfc)inthiscase,andthebypassRCcircuithasthelowestfc.Theoverallresponseisshownastheblueline. 6

7. Total Low-Frequency Response of an Amplifier continue… 7

8. Total Low-Frequency Response of an Amplifier continue…
RefertotheBodeplotinfigure10-26allRCcircuitshavethesamecriticalfrequency,theresponsecurvehasonebreakpointatthatvalueoffc,andthevoltagegainrollsoffat-60dB/decadebelowthatvalue.
Inthiscasethegainisat-9dBbelowthemidrangevoltagegain(-3dBforeachRCcircuit). 8

9. 9

10. 10

11. 11

12. 10-4 High-Frequency Amplifier Response
Wehaveseenthecouplingandbypasscapacitorsaffectthevoltagegainofanamplifieratlowerfrequencieswherethereactancesofthecouplingandbypasscapacitorsaresignificant.
Inmidrangeofanamplifier,theeffectsofthecapacitorsareminimalandcanbeneglected.
Ifthefrequencyisincreasedsufficiently,apointisreachedwherethetransistor’sinternalcapacitancesbegantohaveasignificanteffectonthegain.
12

13. BJT Amplifiers
Ahigh-frequencyacequivalentcircuitfortheBJTamplifierinfig10-31(a)isshowninfig10-31(b).
13

14. BJT Amplifiers continue…
Noticethatthecouplingandbypasscapacitorsaretreatedaseffectiveshortsanddon’tappearinequivalentcircuit.
TheinternalcapacitancesCbeandCbc,whicharesignificantonlyathighfrequencies,doappearinthediagram.
CbeissometimescalledinputcapacitanceCib,andCbcissometimescalledoutputcapacitanceCob.
CbeisspecifiedondatasheetsatacertainvalueofVBE.
OftenthedatasheetwilllistCibasCiboandCobasCobo.
Theoastheletterinthesubscriptindicatesthecapacitanceismeasuredwiththebaseopen. 14

15. Miller’s Theorem in High-Frequency Analysis (in BJT Amplifiers)
Cin(Miller)=Cbc(Av+1)
Cout(Miller)=Cbc(Av+1/Av)
ThesetwoMillercapacitances(Cin(Miller)&Cout(Miller))createahigh-frequencyinputRCcircuitandahigh-frequencyoutputRCcircuit.
Becausethecapacitancesgotogroundandthereforeactaslow-passfilters. 15IdealModelbecausestraycapacitancesduetocircuitinterconnectionsareneglected

16. The Input RC Circuit
Athighfrequencies,theinputcircuitisshowninfig10-33(a) whereRin(base)=βacr'e16

17. The Input RC Circuit continue…
Asthefrequencyincreases,thecapacitivereactancebecomessmaller.Thiscausesthesignalvoltageatbasetodecrease,sotheamplifier’svoltagegaindecreases.
Thereasonforthisisthatthecapacitanceandresistanceactasavoltagedividerand,asthefrequencyincreases,morevoltageisdroppedacrosstheresistanceandlessacrosscapacitance.
Atthecriticalfrequency,thegainis3dBlessthanitsmidrangevalue.
Thecriticalhighfrequency,fc,isthefrequencyatwhichthecapacitivereactanceisequaltothetotalresistance.
XCtot=Rth=Rout=Rs∥R1∥R2∥βacr'e
17

18. The Input RC Circuit continue…
 18Upper critical Frequency

19. 19

20. 20

21. 21

22. Phase Shift of the Input RC Circuit
Becausetheoutputvoltageofahigh-frequencyinputRCcircuitisacrossthecapacitor,theoutputvoltagelagstheinput.Thephaseangleisexpressedas
Atthecriticalfrequencyfc,thephaseangleis45˚withthebase(output)voltagelaggingtheinputsignal.
Asthefrequencyincreasesabove,thephaseangleincreasesabove45˚andapproaches90˚whenthefrequencyissufficientlyhigh. 22

23. The Output RC circuit
Thehigh-frequencyoutputRCcircuitisformedbytheMilleroutputcapacitanceandtheresistancelookinginatthecollectorasshowninfigure10-36(a).
23

24. The Output RC circuit continue…
Cout(Miller)=Cbc(Av+1/Av)
Ifthevoltagegainisatleast10,thenCout(Miller)≈Cbc.
Thecriticalfrequencyisdeterminedas
JustlikeinputRCcircuit,theoutputRCcircuitreducesthegainby3dBatthecriticalfrequency.Whenthefrequencygoesabovethecriticalvalue,thegaindropsat-20dB/decaderate.ThephaseangleintroducedbyoutputRCcircuitis
24Where Rc = RC ∥RL

25. 25

26. 26

27. FET Amplifiers
Theapproachtothehigh-frequencyanalysisofaFETamplifierissimilartothatofaBJT.
ThebasicdifferencesarethespecificationsoftheinternalFETcapacitancesandthedeterminationoftheinputresistance.Figure10-39(a)showsaJFETcommon-sourceamplifierusedtoillustratehigh-frequencyanalysis. 27

28. FET Amplifiers Continue…
Ahigh-frequencyequivalentcircuitfortheamplifierisshowninfigure10-39(b).
Thecouplingandbypasscapacitorsareassumedtohavenegligiblereactancesandareconsideredtobeshorts.
TheinternalcapacitancesCgsandCgdappearintheequivalentcircuitbecausetheirreactancesaresignificantathighfrequencies. 28

29. Values of Cgs, Cgd, and Cds
FETdatasheetsdonotnormallyprovidevaluesforCgs,Cgd, orCds.
InsteadthreeothervaluesareusuallyspecifiedwiththehelpofthemyoucaneasilycalculateCgs,Cgd,andCds.
Cgd=Crss
Cgs=Ciss-Crss
Cds=Coss-Crss
Cossisnotspecifiedasoftenastheothervaluesondatasheets. IncaseswhereCossisnotavailable,youmusteitherassumeavalueorneglectCds. 29Ciss = the input capacitanceCrss = the reverse transfer capacitanceCoss= the output capacitance

30. Miller’s Theorem in High-Frequency Analysis (in FET Amplifiers)
Cin(Miller)=Cgd(Av+1)
Cout(Miller)=Cgd(Av+1/Av)
ThesetwoMillercapacitances(Cin(Miller)&Cout(Miller))createahigh-frequencyinputRCcircuitandahigh-frequencyoutputRCcircuit.
Botharelow-passfilterswhichproducephaselag. 30

31. The Input RC Circuit
Thehigh-frequencyinputcircuitformsalow-passtypeoffilterandisshowninfig-10-41(a).
31

32. The Input RC Circuit Continue…
SincebothRGandRin(gate)ofFETsareextremelyhigh, thereforecontrollingresistancefortheinputcircuitistheresistanceoftheinputsourceRsaslongasRs<<Rin.
ThisisbecauseRsappearsinparallelwithRinwhenThevenin’stheoremisapplied.
ThesimplifiedinputRCcircuitappearsinfigure10-41(b).
Thecriticalfrequencyis: 32

33. 33

34. 34

35. The Output RC circuit
Thehigh-frequencyoutputRCcircuitisformedbytheMilleroutputcapacitanceandtheresistancelookinginatthedrainasshowninfigure10-43(a). 35

36. The Output RC circuit continue…
Cout(Miller)=Cgd(Av+1/Av)
Ifthevoltagegainisatleast10,thenCout(Miller)≈Cgd.
Thecriticalfrequencyisdeterminedas
Theoutputcircuitproducesaphaseshiftof36Where Rd = RD ∥RL

37. 37

38. Total High-Frequency Response of an Amplifier
Wehavealreadyseenthat,twoRCcircuits(Cin(Miller)& Cout(Miller))createdbytheinternaltransistorcapacitancesinfluencethehigh-frequencyresponseofbothBJTandFET.
Asthefrequencyincreasesandreachesthehighendofitsmidrangevalues,oneoftheRCcircuitwillcausetheamplifier’sgaintobegindroppingoff.
Thefrequencyatwhichthisoccursisthedominantcriticalfrequency;itisthelowerofthetwocriticalfrequencies.
Anidealhigh-frequencyBodeplotisshowninfigure10- 44(a)nextslide.Itshowsthefirstbreakpointatfcu(input) wherethevoltagegainbeginstorolloffat-20dB/decade.Atfcu(output),thegainbeginsdroppingat-40dB/decadebecauseeachRCcircuitisaddinga-20dB/decaderoll-off38

39. Total High-Frequency Response of an Amplifier continue…
Figure10-44(b)showsanon-idealBodeplotwherethevoltagegainisactually-3dBbelowmidrangeatfcu(input). OtherpossibilitiesarethattheoutputRCcircuitisdominantorbothcircuitshavethesamecriticalfrequency. 39

40. 10-5 Total Amplifier Frequency Response
Figure10-45(b)nextslideshowsageneralizedidealBodeplotfortheBJTamplifierinfig10-45(a)nextslide.
Thethreebreakpointsatthelowercriticalfrequencies(fcl1,fcl2, andfcl3)areproducedbythreelow-frequencyRCcircuitsformedbythecouplingandbypasscapacitors.
Thetwobreakpointsatthehighercriticalfrequencies(fcu1andfcu2)areproducedbytwohigh-frequencyRCcircuitsformedbythetransistor'sinternalcapacitances.
Thetwodominantcriticalfrequenciesfcl3(fcl(dom))andfcu1(fcu(dom)) areofourinterestinfig10-45(b).
Thesetwofrequenciesarewherethevoltagegainoftheamplifieris3dBbelowitsmidrangevalue.
Thesedominantfrequenciesarereferredtoasthelowercriticalfrequencyfcl(dom),andtheuppercriticalfrequency,fcu(dom).40

41. Total Amplifier Frequency Response Continue… 41

42. Total Amplifier Frequency Response Continue…
Theupperandlowercriticalfrequenciesaresometimescalledthehalf-powerfrequencies.Thisisduetothefactthattheoutputpowerofanamplifieratitscriticalfrequenciesisone-halfofitsmidrangepower(asdiscussedpreviously).
Alsostartingwiththefactthattheoutputvoltageis70.7%ofitsmidrangevalueatthecriticalfrequencies. 42

43. Bandwidth
Anamplifiernormallyoperateswithsignalfrequenciesbetweenfcl(dom)andfcu(dom).
Whentheinputsignalfrequencyisatfcl(dom)orfcu(dom),theoutputsignallevelis70.7%ofitsmidrangevalue.
Ifthesignalfrequencydropsbelowfcl(dom),thegainandthustheoutputsignalleveldrops20dB/decadeuntilthenextcriticalfrequencyisreached.
Thesameoccurswhenthesignalfrequencygoesabovefcu(dom).
Therange(band)offrequencieslyingbetweenfcl(dom)andfcu(dom)isdefinedasthebandwidthoftheamplifierasshowninfigure10- 46nextslide.
Onlythedominantcriticalfrequenciesappearintheresponsecurvebecausetheydeterminethebandwidth. 43

44. Bandwidth Continue…
Theamplifier’sbandwidthisexpressedinunitsofhertzas
BW=fcu(dom)-fcl(dom)
Ideally,allsignalfrequencieslyinginamplifier’sbandwidthareamplifiedequally.i.e,ifa10mVrmssignalisappliedtoanamplifierwithavoltagegainof20,itisamplifiedto200mVrmsforallfrequenciesinthebandwidth. 44

45. Unity-Bandwidth Product
Onecharacteristicofamplifiersisthattheproductofvoltagegainandbandwidthisalwaysconstantwhentherollis-20dB/decade. Thischaracteristiciscalledgain-bandwidthproduct.
Let’sassumethatthelowercriticalfrequencyofaparticularamplifierismuchlessthantheuppercriticalfrequency.
fcl(dom)<<fcu(dom)
Thebandwidthcanbeapproximatedas
BW=fcu(dom)-fcl(dom)≈fcu45

46. Unity-Gain Frequency
ThesimplifiedBodeplotforthecondition(discussedinpreviousslide)isshowninfig10-4746

47. Unity-Gain Frequency Continue…
Noticethatfcl(dom)isneglectedbecauseitissomuchsmallerthanfcu(dom),andthebandwidthapproximatelyequalsfcu(dom).
Beginningatfcu(dom),thegainrollsoffuntilunitygain(0dB)isreached.
Thefrequencyatwhichtheamplifier’sgainis1iscalledtheunity- gainfrequency,fT.
ThesignificanceoffTisthatitalwaysequalsthemidrangevoltagegaintimesthebandwidthandisconstantforagiventransistor.
fT=AV(mid)BW
Forthecaseshowninfig10-47,fT=AV(mid)fcu47

48. 10-6 Frequency Response of Multistage Amplifiers
Whenamplifierstagesarecascadedtoformamultistageamplifier(morethanonestageamplifier),thedominantfrequencyresponseisdeterminedbytheresponsesoftheindividualstages. Therearetwocasestoconsider:
1.Eachstagehasadifferentlowercriticalfrequencyandadifferentuppercriticalfrequency.
2.EachStagehasthesamelowercriticalfrequencyandthesameuppercriticalfrequency.
DifferentCriticalFrequencies
Whenthelowercriticalfrequency,fcl(dom),ofeachamplifierstageisdifferent,thedominantlowercriticalfrequency,f'cl(dom),equalsthecriticalfrequencyofthestagewiththehighestfcl(dom).
Whentheuppercriticalfrequency,fcu(dom),ofeachamplifierstageisdifferent,thedominantuppercriticalfrequency,f'cu(dom),equalsthecriticalfrequencyofthestagewiththelowestfcu(dom). 48

49. Frequency Response of Multistage Amplifiers Continue…
OverallBandwidth
ThebandwidthofamultistageamplifierisBW=f'cu(dom)-f'cl(dom)
EqualCriticalFrequencies
Wheneachamplifierstageinamultistagearrangementhasequalcriticalfrequencies,youmaythinkthatthedominantcriticalfrequencyisequaltothecriticalfrequencyofeachstage.Thisisnotthecasehowever.
Samelowercriticalfrequencies
SameHighercriticalfrequencies
Where“n”isthenumberofstagesofamultistageamplifier. 49

50. 50