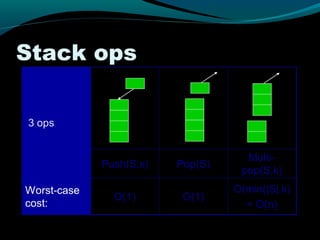
This document discusses amortized analysis, which analyzes the average cost per operation of a sequence of operations, even if some operations are individually expensive. It describes three methods for amortized analysis: aggregate, accounting, and potential. The aggregate method bounds the total cost of n operations to show the average cost per operation is small. The accounting method assigns different costs to operations, using credit from low-cost operations to pay for high-cost ones. The potential method associates potential energy with the data structure to pay for future expensive operations. Examples of applications like vectors and priority queues are also given.

1. Amortized Analysis
By Waqas Shehzad
Fast NU Pakistan

2. Amortized Analysis
An amortized analysis is any
strategy for analyzing a sequence of
operations to show that the average
cost per operation is small, even
though a single operation within the
sequence might be expensive.
Even though we’re taking averages,
however, probability is not involved!

3. Operations on Data
Structures
A data structure has a set of operations
associated with it.
Example: A stack with
push(), pop() and MultiPop(k).
Often some operations may be slow
while others are fast.
push() and pop() are fast.
MultiPop(k) may be slow.
Sometimes the time of a single
operation can vary

4. Amortized Analysis
Aggregate Method: we determine an upper
bound T(n) on the total sequence of n
operations. The cost of each will then be
T(n)/n.
Accounting Method: we overcharge some
operations early and use them to as prepaid
charge later.
Potential Method: we maintain credit as
potential energy associated with the structure
as a whole.

5. Aggregate Method
We show that for n operation, the sequence
takes worst case T(n)
We use as an example, a stack with a new
operation MULTIPOP (S,k)
If we consider PUSH and POP to be elementary
operations, then Multipop takes O(n) in the worst
case.

6. Stack ops

7. Stack - aggregate
analysis
Push and Pop are O(1) (to move 1 data element)
Multipop is O(min(s, k)) where
s is the size of the stack and
k the number of elements to pop.
Assume a sequence of n Push, Pop and Multipop
operations
Multipop(S, k)
while not empty(S) and k>0 do
Pop(S);
k:=k-1
end while
7

8. Aggregate Method
• Sequence of n push, pop, Multipop operations
• Worst-case cost of Multipop is O(n)
• Have n operations
• Therefore, worst-case cost of sequence is
O(n2)
However, since an object can be only popped
once (whether by pop or multipop) for every
time it is pushed, the total number of Pop
operations is at most the total number of Push
operations (which is at most n)

9. Stack - aggregate
analysis
A sequence of n Push and Pop
operations is therefore O(n) and the
amortized cost of each is
O(n)/n=O(1)

10. Accounting Method
We assign different charges to different
operations, with some operations charged
more or less than they actually cost.
The amount we charge an operation is its
amortized cost.
When an operation’s amortized cost exceeds
its actual cost, the difference is assigned to
specific objects in the data structure as credit.

11. Accounting Method
Credit can be used later to pay the cost of
operations whose actual cost is greater than
its amortized cost.
The total credit stored must always be non-
negative at all times.
We must ensure that
n n
∑ ci ≤ ∑ ci
ˆ
i =1 i =1
Amortized cost ĉi

12. Accounting Method: Stack
Thing about this: when we push a plate onto
a stack, we use $1 to pay actual cost of the
push and we leave $1 on the plate.
At any point, every plate on the stack has a
dollar on top of it.
When we execute a pop operation, we
charge it nothing and pay its cost with the
dollar that is on top of it.

13. A Simple Example: Accounting
3 ops:
Push(S,x) Pop(S) Multi-pop(S,k)
•Assigned
2 0 0
cost:
•Actual cost: 1 1 min(|S|,k)

14. Potential Method
Instead of representing prepaid work as credit
stored with specific objects, the potential method
represents the prepaid work as potential energy
than can be released to pay for future
operations.
Potential is associated with the data structure as
a whole rather than with specific objects.

15. Potential Method
We start with an initial data structure D0 on which
n operations are performed.
Let ci be the cost the ith operations and Di be the
data structure that results after applying the ith
operation to data structure Di-1
A potential function Φ maps Di to a real number
Φ(Di) which is the potential associated with Di

16. Applications of
amortized analysis
Vectors/ tables
Disjoint sets
Priority queues
Heaps, Binomial heaps, Fibonacci heaps
Hashing