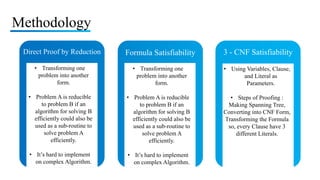
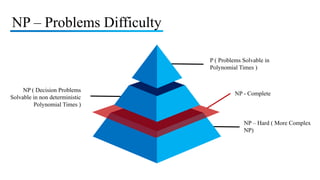
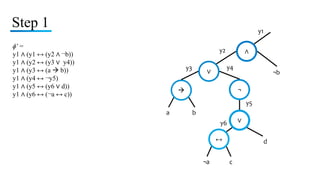
The document discusses NP-completeness and provides examples of NP-complete problems. It begins by introducing NP-completeness and the concepts of P, NP, NP-hard, and NP-complete problems. It then discusses the Boolean satisfiability problem and shows that 3-CNF satisfiability is NP-complete by providing a proof of reduction. Finally, it discusses the vertex cover problem and proves that it is NP-complete by reducing it from the NP-complete clique problem. In summary, the document introduces NP-completeness and provides proofs that 3-CNF satisfiability and the vertex cover problem are NP-complete problems.

1. NP-Completeness
Proof

2. Introduction
Formula Satisfiability
3 – CNF Satisfiability
Problems Set

3. Introduction
*picture taken from https://www.express.co.uk/news/science/1021070/end-of-the-world-universe-Geraint-Lewis-science-new-scientist-live on May, 2019

4. Methodology
Direct Proof by Reduction Formula Satisfiability 3 - CNF Satisfiability
• Transforming one
problem into another
form.
• Problem A is reducible
to problem B if an
algorithm for solving B
efficiently could also be
used as a sub-routine to
solve problem A
efficiently.
• It’s hard to implement
on complex Algorithm.
• Transforming one
problem into another
form.
• Problem A is reducible
to problem B if an
algorithm for solving B
efficiently could also be
used as a sub-routine to
solve problem A
efficiently.
• It’s hard to implement
on complex Algorithm.
• Using Variables, Clause,
and Literal as
Parameters.
• Steps of Proofing :
Making Spanning Tree,
Converting into CNF Form,
Transforming the Formula
so, every Clause have 3
different Literals.

5. NP – Problems Difficulty
P ( Problems Solvable in
Polynomial Times )
NP ( Decision Problems
Solvable in non deterministic
Polynomial Times )
NP – Hard ( More Complex
NP)
NP - Complete

6. Formula
Satisfiability
*picture taken from https://www.coe.int/en/web/bern-convention/documents on May, 2019

7. Description
We formulate the (formula) satisfiability problem in terms of the language SAT as follows. An
instance of SAT is a boolean formula ɸ composed of
• n boolean variables: x1, x2, x3….,xn .
• m boolean connectives: any boolean function with one or two inputs and one output, such as
˄ (AND), ˅ (OR), ¬(NOT), →(implication), ↔ (if and only if).
• parentheses. (Without loss of generality, we assume that there are no redundant parentheses,
i.e.,aformula contains atmostone pair ofparentheses per boolean connective).

8. Equation
Notes :
SAT = {( ɸ ) : ɸ is a satisfiable boolean
formula}

9. 3 – CNF
Satisfiability
*picture taken from https://www.analyticsindiamag.com/6-types-of-artificial-neural-networks-currently-being-used-in-todays-technology/ on May, 2019

10. Description
Boolean Formula can be categorized as CNF if it’s having 3 different Literal and meet the terms
of requirement of 3 – CNF Satisfiability:
• Variable that affected the Formula, usually notated using alphabet.
• Literal is an event that occurs from it’s variable or negation.
• Clause is a disjunction ( OR ) from Literal.
• Conjunctive Normal Form ( CNF ) Formula is a Conjunction ( AND ) from several Clause.

11. Lemma
Satisfiability of 3 – CNF Boolean Formula is a NP – Complete.
Proof :
Algorithm Reduction is mainly divided into 3 main steps, which every step making the formula
of ɸ come up into 3 – CNF. It can be described like this :
• Making tree from formula ɸ inputs, into formula and clause of ɸ’ with each of them having
maximum 3 numbers of Literal.
• Converting every ɸ’into CNF.
• Transforming the formula, so every Clause having 3 Literals.

12. Example
Problem :
Show that ɸ = (a ∨ b ∨ c) ∧ (¬b ∨ c ∨ d) ∧ (a ∨ ¬b ∨ ¬c) is 3 – CNF Satisfiability!
Answer :
(a ∨ b ∨ c) ∧ (¬b ∨ c ∨ d) ∧ (a ∨ ¬b ∨ ¬c) is 3 – CNF because it’s a conjunction from 3 clause
and each clause have different Literal. That can be described like this :
• a, b, c, d is Variables.
• a, b, ¬b, c, ¬c, d is Literals.
• a ∨ b ∨ c is Clause.
• So, (a ∨ b ∨ c) ∧ (¬b ∨ c ∨ d) is CNF.

13. Problem :
Show that ɸ = ((a  b) ∨ ¬((¬a ↔ c) ∨ d)) ∧ ¬b is 3 – CNF Satisfiability!
Answer :
Step 1 ; Making Spanning Tree
Step 2 : Converting into CNF Form.
Step 3 : Transforming the Formula so, every Clause have 3 different Literals.
Example

14. Step 1
ɸ’ =
y1 ∧ (y1 ↔ (y2 ∧ ¬b))
y1 ∧ (y2 ↔ (y3 ∨ y4))
y1 ∧ (y3 ↔ (a  b))
y1 ∧ (y4 ↔ ¬y5)
y1 ∧ (y5 ↔ (y6 ∨ d))
y1 ∧ (y6 ↔ (¬a ↔ c))
¬a c
↔ d
∨y6
¬
y5
a b

∨
y4y3
¬b
∧y2
y1

15. Step 2
y1 y2 b (y1 ↔ (y2 ∧ ¬b))
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 1
Truth Table

16. Step 2
From that truth table, we can get DNF (disjunctive normal form)
¬ɸ1’ = (y1 ∧ y2 ∧ b) ∨ (y1 ∧ ¬ y2 ∧ b) ∨(y1 ∧ ¬ y2 ∧ ¬ b) ∨ (¬ y1 ∧ y2 ∧ ¬ b)
ɸ1’’ = (¬ y1 ∨ ¬ y2 ∨ ¬ b) ∧ (¬ y1 ∨ y2 ∨ ¬ b) ∧ (¬ y1 ∨ y2 ∨ b) ∧ (y1 ∨ ¬ y2 ∨ b)

17. Step 3
Making 3 – CNF Formula of ɸ’’’ from all of clause that already in ɸ’’. ɸ’’’ also using 2 auxiliary
Variable such as p and q. For every clause Ci from ɸ’’, inserted into ɸ’’’ clause with :
• If Ci having 3 different Literals, insert Ci into ɸ’’’.
• If Ci having 2 different Literals, maybe Ci = (l1 ∨ l2), insert (l1 ∨ l2 ∨ p) ∧ (l1 ∨ l2 ∨ ¬p)
into ɸ’’’.
• If Ci only having 1 Literal, then insert (l ∨ p ∨ q) ∧ (l ∨ p ∨ ¬ q) ∧ (l ∨ ¬ p ∨ q) ∧ (l ∨ ¬ p ∨
¬ q) into ɸ’’’.

18. Problems Set
*picture taken from https://www.collegeparentcentral.com/2010/02/is-your-college-student-investing-enough-time-studying/on May, 2019

19. Preface
A Decision Problem is NP-Complete if :
• L is in NP (A problem is NP if it can be solved by a Non-deterministic Turing Machine in
Polynomial time).
• Every problem in NP is reducible to L in polynomial time.

20. Vertex Cover Problem
A Vertex Cover of an undirected graph is a subset of its vertices such that for every edge (u, v)
of the graph, either ‘u’ or ‘v’ is in vertex cover. Although the name is Vertex Cover, the set
covers all edges of the given graph. Given an undirected graph, the vertex cover problem is to
find minimum size vertex cover.

21. Proof of NP
• V’ is a subset of V.
• The Instance of the problem is Graph G(V, E) and a positive integer K.
• The following strategy can be used to identify if V’ is a Vertex Cover of size k.
• The solution given can be solved within polynomial time.
let count be an integer
set count to 0 f
or each vertex v in V’
remove all edges adjacent to v from set E
increment count by 1
if count = k and E is empty
then
the given solution is correct
else
the given solution is wrong

22. Proof of NP - Hard
• By reducing a problem that is known to be an NP-Hard Problem to the Vertex Cover Problem,
we can prove its NP-Hardness.
• We use the Clique Problem for this, which is an NP-Complete Problem and therefore NP-Hard.

23. Clique Problem
• The Clique Problem is the computational
problem of finding cliques ( subsets of
vertices, all adjacent to each other, also
called complete subgraphs ) in a graph.
• An example of how a brute-force
algorithm finding a 4-clique in a 7-vertex
graph is shown.

24. Proof of NP Hard using Clique Problem
• An instance of the Clique Problem is Graph G(V,E) and a non-negative integer k.
• Consider G’ as a compliment of G
• The problem of finding whether a clique of size k exists in the graph G is the same as the
problem of finding whether there is a vertex cover of size |V| – k in G’
• Let V’ be the set of Cliques with a size of k, this means |V’| = k.
• The set of cliques of G’ is V’’ = V – V’, because of its compliments
• Consider V’’ of size |V| - k is the vertex cover of G’

25. Bibliography and
References
*picture taken from http://fortune.com/2015/09/24/ebook-sales/ on April, 2019

26. Thomas H. Cormen, “Introduction to Algorithms”,
3rd Edition, MIT Press, 2009. ( Page 1078 – 1086 )
"Proof that vertex cover is NP complete -
GeeksforGeeks", GeeksforGeeks, 2019. [Online].
Available: https://www.geeksforgeeks.org/proof-that-
vertex-cover-is-np-complete/. [Accessed: 06- May-
2019]
"Vertex Cover Problem | Set 1 (Introduction and
Approximate Algorithm) -
GeeksforGeeks", GeeksforGeeks, 2019. [Online].
Available: https://www.geeksforgeeks.org/vertex-
cover-problem-set-1-introduction-approximate-
algorithm-2/. [Accessed: 06- May- 2019]
"Two Clique Problem (Check if Graph can be divided
in two Cliques) - GeeksforGeeks", GeeksforGeeks,
2019. [Online]. Available:
https://www.geeksforgeeks.org/two-clique-problem-
check-graph-can-divided-two-cliques/. [Accessed: 06-
May- 2019]
[1]
[2]
[3]
[4]