Download to read offline
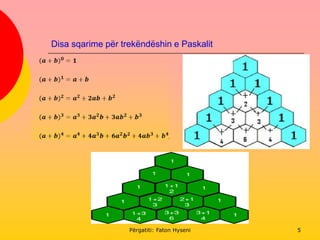
Formula e binomit
- 1.
- 2. Rikujtojmë formulat përfuqitë përkatëse të binomit: 𝒂 + 𝒃 𝟎 = 𝟏 𝒂 + 𝒃 𝟏 = 𝒂 + 𝒃 𝒂 + 𝒃 𝟐 = 𝒂 𝟐 + 𝟐𝒂𝒃 + 𝒃 𝟐 𝒂 + 𝒃 𝟑 = 𝒂 𝟑 + 𝟑𝒂 𝟐 𝒃 + 𝟑𝒂𝒃 𝟐 + 𝒃 𝟑 𝒂 + 𝒃 𝟒 = 𝒂 𝟒 + 𝟒𝒂 𝟑 𝒃 + 𝟔𝒂 𝟐 𝒃 𝟐 + 𝟒𝒂𝒃 𝟑 + 𝒃 𝟒 , etj Gjithashtu rikujtojmë se: 𝐂 𝐧 𝐤 = 𝐧! 𝐤! 𝐧−𝐤 ! = 𝐧 𝐤 , ku 𝒏 𝟎 = 𝟏 dhe 𝒏 𝒏 = 𝟏 . Përgatiti: Faton Hyseni 2
- 3. Nëse në formulate mësipërme, koeficientët i shkruajmë në trajtë të koeficientëve të binomit 𝑛 𝑘 , kemi: 𝒂 + 𝒃 𝟎 = 𝟎 𝟎 = 𝟏 𝒂 + 𝒃 𝟏 = 𝟏 𝟎 𝒂 + 𝟏 𝟏 𝒃 = 𝒂 + 𝒃 𝒂 + 𝒃 𝟐 = 𝟐 𝟎 𝒂 𝟐 + 𝟐 𝟏 𝒂𝒃 + 𝟐 𝟐 𝒃 𝟐 =𝒂 𝟐 + 𝟐𝒂𝒃 + 𝒃 𝟐 𝒂 + 𝒃 𝟑 = 𝟑 𝟎 𝒂 𝟑 + 𝟑 𝟏 𝒂 𝟐 𝒃 + 𝟑 𝟐 𝒂𝒃 𝟐 + 𝟑 𝟑 𝒃 𝟑 = 𝒂 𝟑 + 𝟑𝒂 𝟐 𝒃 + 𝟑𝒂𝒃 𝟐 + 𝒃 𝟑 𝒂 + 𝒃 𝟒 = 𝟒 𝟎 𝒂 𝟒 + 𝟒 𝟏 𝒂 𝟑 𝒃 + 𝟒 𝟐 𝒂 𝟐 𝒃 𝟐 + 𝟒 𝟑 𝒂𝒃 𝟑 + 𝟒 𝟒 𝒃 𝟒 = 𝒂 𝟒 + 𝟒𝒂 𝟑 𝒃 + 𝟔𝒂 𝟐 𝒃 𝟐 + 𝟒𝒂𝒃 𝟑 + 𝒃 𝟒 , etj . Përgatiti: Faton Hyseni 3
- 4. Në përgjithësi nëse𝑛 është numër natyror, atëherë: 𝒂 + 𝒃 𝒏 = 𝒏 𝟎 𝒂 𝒏 + 𝒏 𝟏 𝒂 𝒏−𝟏 𝒃 + 𝒏 𝟐 𝒂 𝒏−𝟐 𝒃 𝟐 + ⋯ + 𝒏 𝒌 𝒂 𝒏−𝒌 𝒃 𝒌 + ⋯ + 𝒏 𝒏 𝒃 𝒏 e cila quhet formula e binomit ose e Njutonit. Formula e mësipërme mund të shkruhet shkurtimisht në këtë mënyrë: 𝒂 + 𝒃 𝒏 = 𝒌=𝟎 𝒏 𝒏 𝒌 𝒂 𝒏−𝒌 𝒃 𝒌 ku 𝒏 𝒌 = 𝒏! 𝒌! 𝒏−𝒌 ! ( simboli ∑ lexohet sigma dhe paraqet shumën ) Koeficientët e binomit, të cilët paraqiten në formulën e binomit, janë numra natyror dhe mund të fitohen edhe me ndihmën e trekëndëshit të Paskalit: Përgatiti: Faton Hyseni 4
- 5. Disa sqarime përtrekëndëshin e Paskalit Përgatiti: Faton Hyseni 5
- 6. Raste tjera përtrekëndëshin e Paskalit Përgatiti: Faton Hyseni 6 Shembull
- 7. Raste tjera përtrekëndëshin e Paskalit Përgatiti: Faton Hyseni 7
- 8. Raste tjera përtrekëndëshin e Paskalit Përgatiti: Faton Hyseni 8
- 9. Shembulli 1 Përgatiti: FatonHyseni 9
- 10. Shembulli 2 Përgatiti: FatonHyseni 10
- 11. Shembulli 3 Përgatiti: FatonHyseni 11
- 12. Shembulli 4 Përgatiti: FatonHyseni 12
- 13. Shembulli 5 Përgatiti: FatonHyseni 13
- 14. Shembulli 6 Përgatiti: FatonHyseni 14
- 15. Shembulli 7 Gjeni termine tretë të zbërthimit të 𝑥 − 3 𝑦 10 . Zgjidhje 𝒙 + 𝒚 𝒏 = 𝒌=𝟎 𝒏 𝒏 𝒌 𝒙 𝒏−𝒌 𝒚 𝒌 𝒙 − 𝟑 𝒚 𝟏𝟎 = 𝒌=𝟎 𝟏𝟎 𝟏𝟎 𝒌 𝒙 𝟏𝟎−𝒌 −𝟑 𝒚 𝒌 Termi i tretë i zbërthimit të 𝑥 − 3 𝑦 10 do të jetë për 𝑘 = 2, prandaj 10 2 𝑥10−2 −3 𝑦 2 = 10! 2!8! 𝑥8 ∙ 9 ∙ 𝑦 = 10∙9 2 𝑥8 ∙ 9 ∙ 𝑦 = 405𝑥8 𝑦 . D.m.th. 405𝑥8 𝑦 është termi i tretë. Përgatiti: Faton Hyseni 15