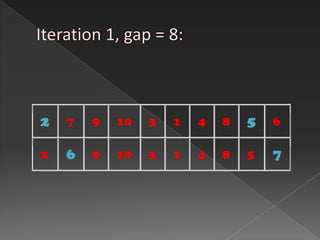
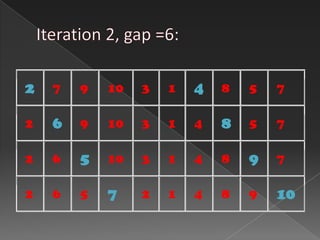
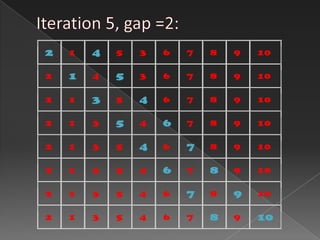
Comb sort is a sorting algorithm that improves on bubble sort by allowing larger gaps between elements to be compared. It starts with a large gap that shrinks on each iteration. This eliminates more swaps than bubble sort and moves high and low values towards their final positions more quickly. Rabbits refer to large values at the beginning, and turtles to small values at the end, which comb sort handles more efficiently than bubble sort.

1. COMB SORTING

2.  The basic idea is to eliminate turtles, or small
values near the end of the list, Since in a
bubble sort these slow the sorting down
tremendously. Rabbits, large values around the
beginning of the list, do not pose a problem in
bubble sort.

3.  Instead of comparing adjacent elements, comb
sort allows for a larger gap between elements.
 This eliminates the number of required swaps.
 We get small numbers at the end to reach
beginning of the list.
 In bubble sort, when any two elements are
compared, they always have a gap (distance
from each other) of 1.
 The basic idea of comb sort is that the gap can
be much more than 1

4.  Rabbits & turtles: RABBITS are the elements
with the large values located near the
beginning while TURTLES are the elements
with the small values located near the end of
the list.
 Gap size the distance b/w two elements
 Shrink Factor usually taken 1.3

5.  Begin with a gap size equal to n
 Recalculate the gap size by dividing the
previous gap size by a shrink factor
 Iterate through the list, swapping elements
 If the gap is currently 1 and no swap is
occurred during this iteration, then the list is
sorted.
 Otherwise repeat.

6. Unsorted list
:
5 7 9 10 3 1 4 8 2 6

7. 2 7 9 10 3 1 4 8 5 6
2 6 9 10 3 1 4 8 5 7

8. 2 7 9 10 3 1 4 8 5 7
2 6 9 10 3 1 4 8 5 7
2 6 5 10 3 1 4 8 9 7
2 6 5 7 2 1 4 8 9 10

9. 2 7 9 10 3 1 4 8 5 10
2 1 9 10 3 6 4 8 5 10
2 1 4 10 3 6 5 8 9 10
2 1 4 7 3 6 5 8 9 10
2 1 4 7 3 6 5 8 9 10
2 1 4 7 3 6 5 8 9 10

10. 2 1 4 7 3 6 5 8 9 10
2 1 4 7 3 6 5 8 9 10
2 1 4 7 3 6 5 8 9 10
2 1 4 5 3 6 7 8 9 10
2 1 4 5 3 6 5 8 9 10
2 1 4 5 3 6 5 8 9 10
2 1 4 5 3 6 7 8 9 10

11. 2 1 4 5 3 6 7 8 9 10
2 1 4 5 3 6 7 8 9 10
2 1 3 5 4 6 7 8 9 10
2 1 3 5 4 6 7 8 9 10
2 1 3 5 4 6 7 8 9 10
2 1 3 5 4 6 7 8 9 10
2 1 3 5 4 6 7 8 9 10
2 1 3 5 4 6 7 8 9 10

12. 1 2 3 5 4 6 7 8 9 10
1 2 3 5 4 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
2 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10

13. 1 2 3 4 5 6 7 8 9 10

14. void combSort(int a[], int len)
{
int gap = len;
bool swapped;
do{
swapped = false;
gap = newGap(gap);
for(int i=0; i < len-gap; ++i){
if(a[i] > a[i+gap]){
swapped = true;
swap(a[i], a[i+gap]);
}
}
}while(gap > 1 || swapped);
for(int i=0;i<len;i++)
cout<<" "<<a[i];
}

15.  http://xlinux.nist.gov/dads/HTML/combSort.
html
 http://en.wikipedia.org/wiki/Comb_sort