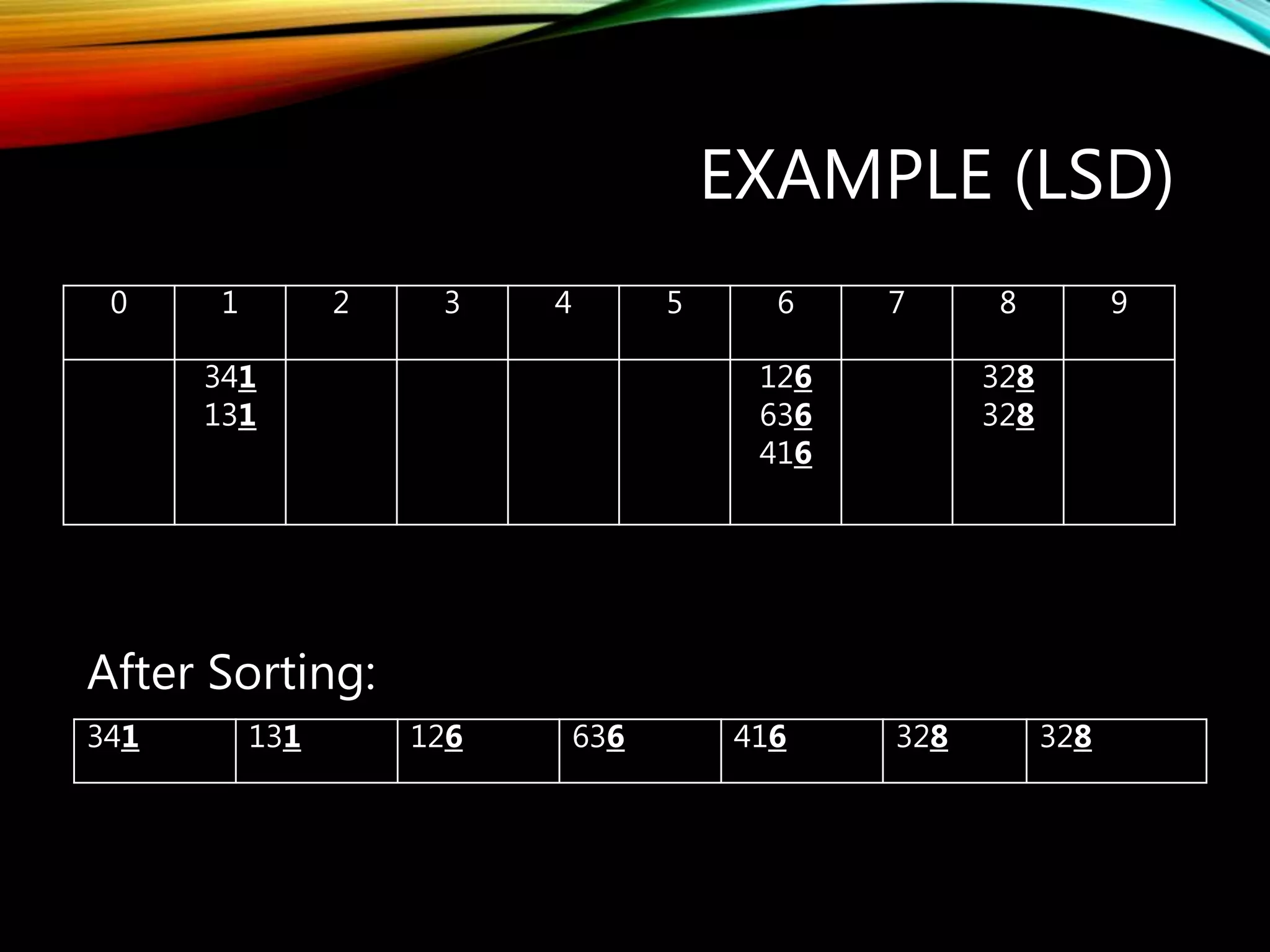
Radix sort is a non-comparative sorting algorithm that sorts data by grouping keys based on individual digit values. It uses bucket sort repeatedly on each digit place value, from least to most significant. This requires a number of passes equal to the maximum digit length. Each pass takes O(n+k) time, so the total time complexity is O(d(n+k)) where d is the digit length. Radix sort is very efficient and requires minimal space and data movement compared to other algorithms.

1. RADIX SORT
ADA (2150703)
Presented by,
Arafat Tai
150410107114
S.Y. CE-II Batch : C

2. Radix Means : The base of a system of
numeration
Examples:
• The decimal number system that we use every day has 10
digits {0,1,2,3,4,5,6,7,8,9} and so the radix is 10.

3. RADIX SORT
 Radix sort is generalization of bucket sort.
 It uses several passes of bucket sort.
 Radix sort is stable and fast.

4. • In Computer Science Radix Sort is a non –
comparative integer sorting algorithm that sort
data with integer keys by grouping keys by the
individual digits which share same significant
position and value.

5. RADIX SORT
• Unlike other sorting algorithms Radix sort is not
based on the general algorithm strategy above,
but on a totally different method. It is
interesting because it requires the absolute
minimum amount of space and the minimum
amount of data movement, and, most amazing
of all, it does no comparisons.

6. CLASSIFICATIONS
1. Least Significant Digit (LSD) radix sorts
2. Most Significant Digit (MSD) radix sorts

7. LEAST SIGNIFICANT DIGIT
(LSD) RADIX SORTS
 How many times we will sort the number ?
or
How many passes will required ?

8. LEAST SIGNIFICANT DIGIT
(LSD) RADIX SORTS
Examples :
4310 , 357 , 251 , 78

9. LEAST SIGNIFICANT DIGIT
(LSD) RADIX SORTS
Examples :
4310 , 357 , 251 , 78
So 4 passes will require .
4310

10. EXAMPLE (LSD)
126 328 636 341 416 131 328
Input list :

11. EXAMPLE (LSD)
126 328 636 341 416 131 328
BinSort on lower digit / Pass
1 :

12. EXAMPLE (LSD)
126 328 636 341 416 131 328
BinSort on lower digit / Pass
1 :
0 1 2 3 4 5 6 7 8 9

13. EXAMPLE (LSD)
126 328 636 341 416 131 328
BinSort on lower digit:
0 1 2 3 4 5 6 7 8 9
126

14. EXAMPLE (LSD)
126 328 636 341 416 131 328
BinSort on lower digit:
0 1 2 3 4 5 6 7 8 9
126 328

15. EXAMPLE (LSD)
126 328 636 341 416 131 328
BinSort on lower digit:
0 1 2 3 4 5 6 7 8 9
126
636
328

16. EXAMPLE (LSD)
126 328 636 341 416 131 328
BinSort on lower digit:
0 1 2 3 4 5 6 7 8 9
341 126
636
328

17. EXAMPLE (LSD)
126 328 636 341 416 131 328
BinSort on lower digit:
0 1 2 3 4 5 6 7 8 9
341 126
636
416
328

18. EXAMPLE (LSD)
126 328 636 341 416 131 328
BinSort on lower digit:
0 1 2 3 4 5 6 7 8 9
341
131
126
636
416
328

19. EXAMPLE (LSD)
126 328 636 341 416 131 328
BinSort on lower digit:
0 1 2 3 4 5 6 7 8 9
341
131
126
636
416
328
328

20. EXAMPLE (LSD)
341 131 126 636 416 328 328
After Sorting:
0 1 2 3 4 5 6 7 8 9
341
131
126
636
416
328
328

21. EXAMPLE (LSD)
BinSort on next higher digit / Pass 2 :
341 131 126 636 416 328 328

22. EXAMPLE (LSD)
BinSort on next higher digit:
0 1 2 3 4 5 6 7 8 9
341
341 131 126 636 416 328 328

23. EXAMPLE (LSD)
BinSort on next higher digit:
0 1 2 3 4 5 6 7 8 9
131 341
341 131 126 636 416 328 328

24. EXAMPLE (LSD)
BinSort on next higher digit:
0 1 2 3 4 5 6 7 8 9
126 131 341
341 131 126 636 416 328 328

25. EXAMPLE (LSD)
BinSort on next higher digit:
0 1 2 3 4 5 6 7 8 9
126 131
636
341
341 131 126 636 416 328 328

26. EXAMPLE (LSD)
BinSort on next higher digit:
0 1 2 3 4 5 6 7 8 9
416 126 131
636
341
341 131 126 636 416 328 328

27. EXAMPLE (LSD)
BinSort on next higher digit:
0 1 2 3 4 5 6 7 8 9
416 126
328
131
636
341
341 131 126 636 416 328 328

28. EXAMPLE (LSD)
BinSort on next higher digit:
0 1 2 3 4 5 6 7 8 9
416 126
328
328
131
636
341
341 131 126 636 416 328 328

29. EXAMPLE (LSD)
416 126 328 328 636 131 341
After Sorting:
0 1 2 3 4 5 6 7 8 9
416 126
328
328
636 341

30. EXAMPLE (LSD)
416 126 328 328 131 636 341
BinSort on next higher or highest digit /
Pass 3 :

31. EXAMPLE (LSD)
416 126 328 328 131 636 341
BinSort on next higher/highest
digit:
0 1 2 3 4 5 6 7 8 9
416

32. EXAMPLE (LSD)
416 126 328 328 131 636 341
BinSort on next higher/highest
digit:
0 1 2 3 4 5 6 7 8 9
126 416

33. EXAMPLE (LSD)
416 126 328 328 131 636 341
BinSort on next higher/highest
digit:
0 1 2 3 4 5 6 7 8 9
126 328 416

34. EXAMPLE (LSD)
416 126 328 328 131 636 341
BinSort on next higher/highest
digit:
0 1 2 3 4 5 6 7 8 9
126 328
328
416

35. EXAMPLE (LSD)
416 126 328 328 131 636 341
BinSort on next higher/highest
digit:
0 1 2 3 4 5 6 7 8 9
126
131
328
328
416

36. EXAMPLE (LSD)
416 126 328 328 131 636 341
BinSort on next higher/highest
digit:
0 1 2 3 4 5 6 7 8 9
126
131
328
328
416 636

37. EXAMPLE (LSD)
416 126 328 328 131 636 341
BinSort on next higher/highest
digit:
0 1 2 3 4 5 6 7 8 9
126
131
328
328
341
416 636

38. EXAMPLE (LSD)
126 131 328 328 341 416 636
After Sorting:
0 1 2 3 4 5 6 7 8 9
126
131
328
328
341
416 636

39. EXAMPLE (LSD)
126 131 328 328 341 416 636
Completed

40. EXAMPLE (LSD)
126 131 328 328 341 416 636
The Numbers are now sorted

41. ALGORITHM
1.Create an array a[ 0…..n-1] elements.
2.Call bucket sort repeatedly on least to most
significant digit of each element as the key.
3.Return the sorted array.

42. ANALYSIS
Each pass over n d-digit numbers and k base
keys then takes time O(n+k). (Assuming
counting sort is used for each pass.)
There are d passes, so the total time for radix
sort is O(d (n+k)).
When d is a constant and total run time = O(n)

43. COMPLEXITY ANALYSIS:
The complexity is O((n+b)∗logb(maxx))
where b is the base for representing numbers
and maxx is the maximum element of the input
array. This is clearly visible as we make (n+b)
iterations logb(maxx) times (number of digits in
the maximum element) . If maxx ≤ n^c , then
the complexity can be written as O(n∗logb(n)).

44. SOURCES
 GeeksForGeeks
 Wikipedia
 Hakerearth

45. Questions ?

46. Thank You