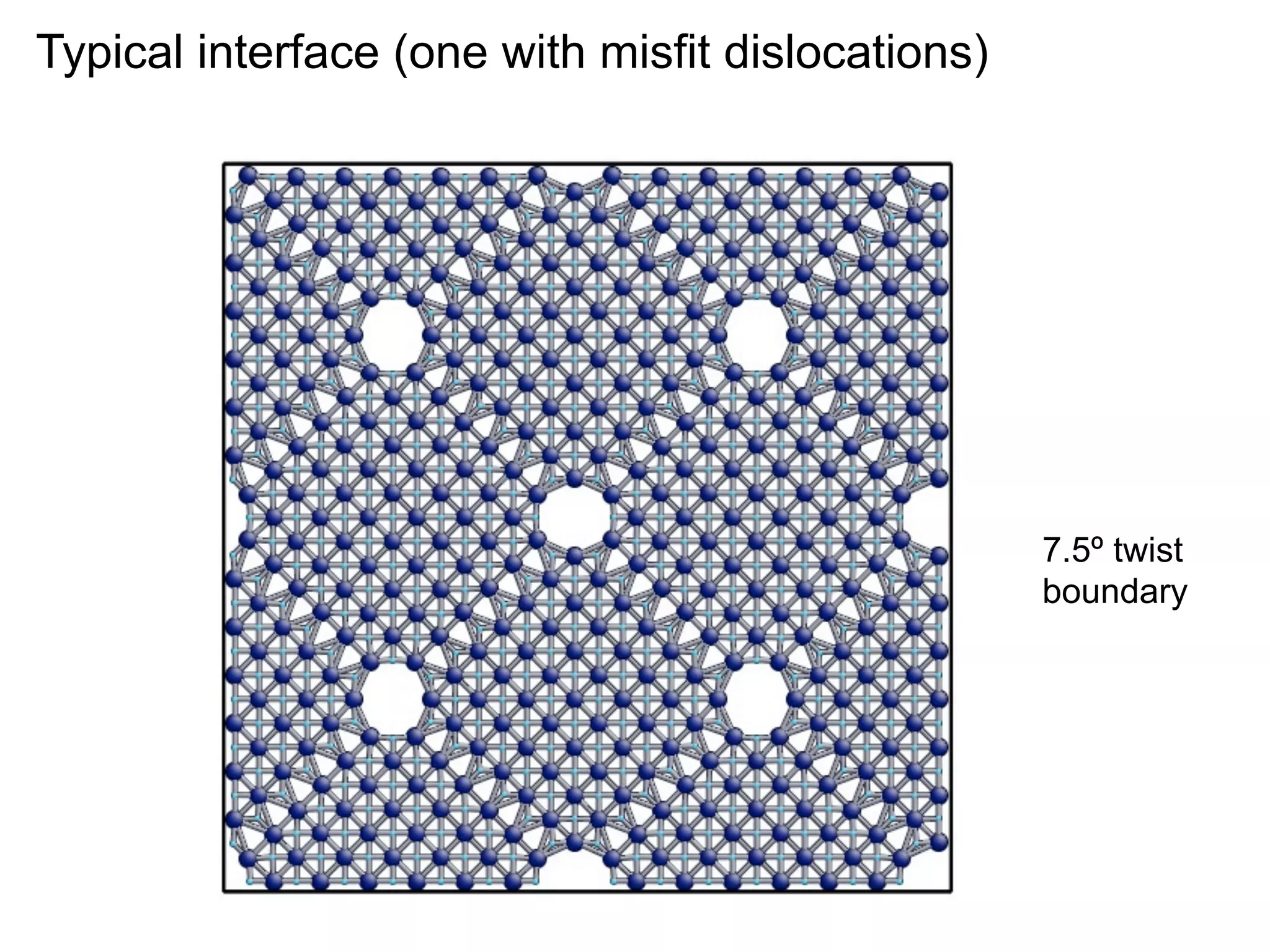
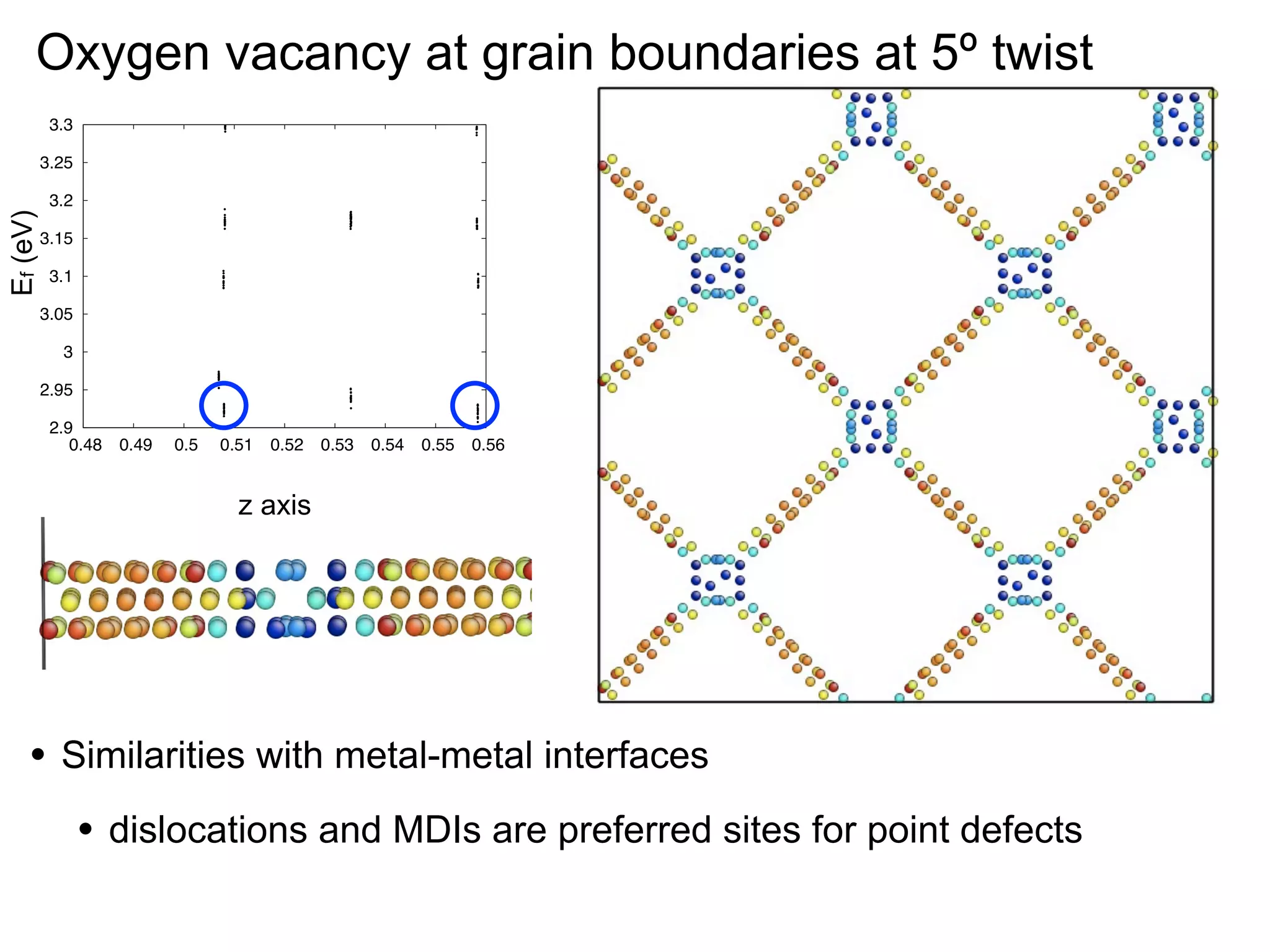
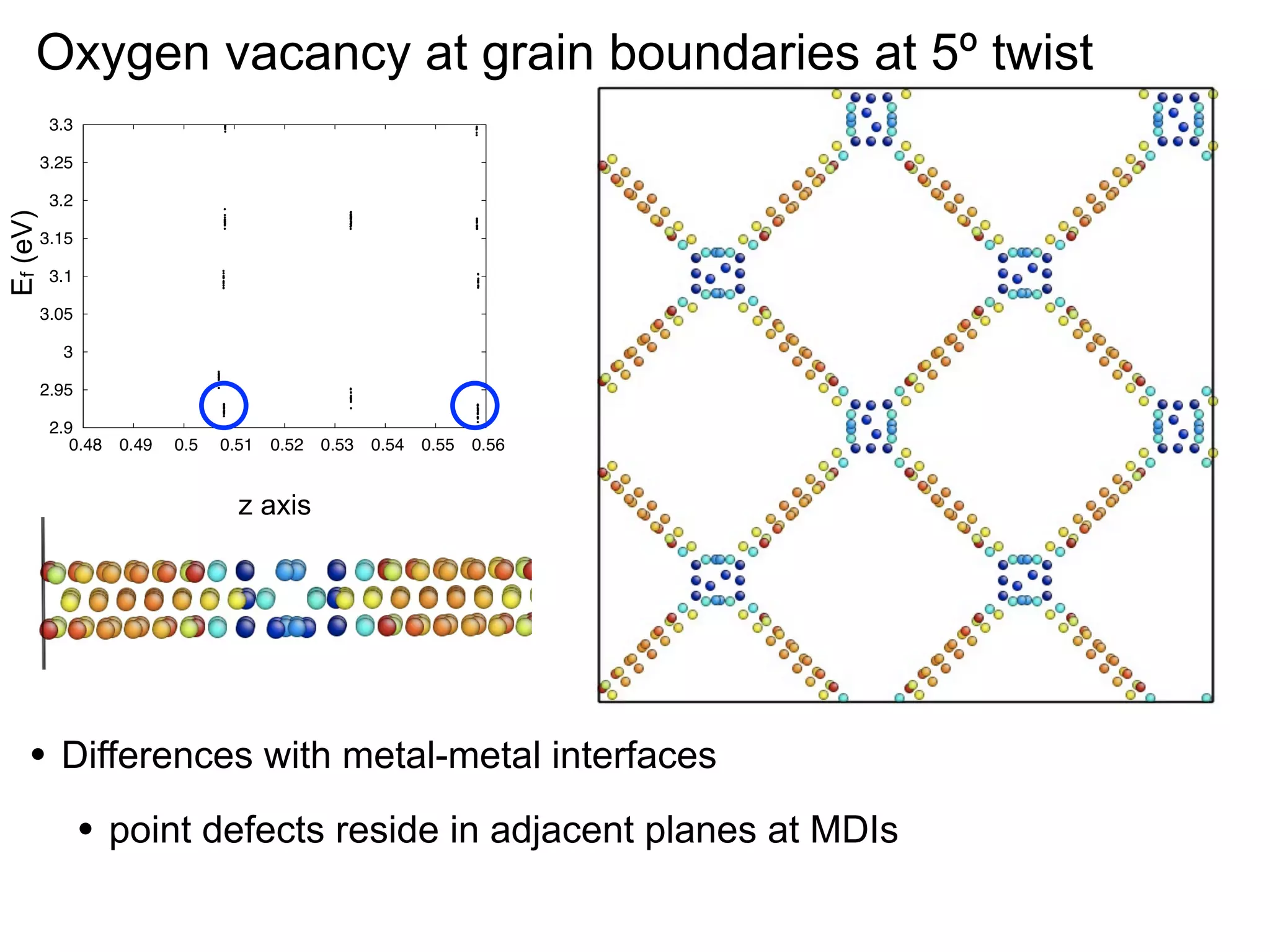
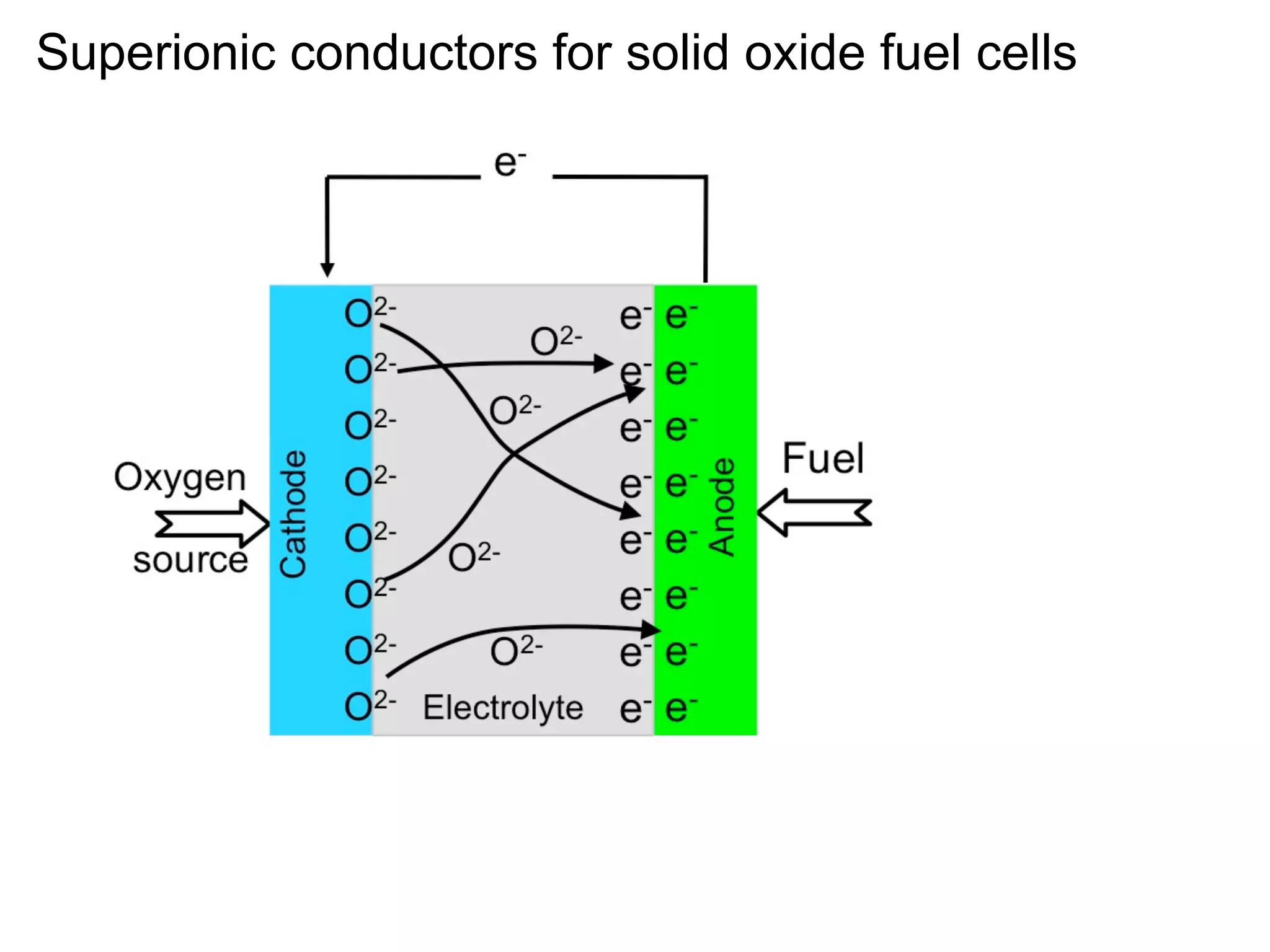
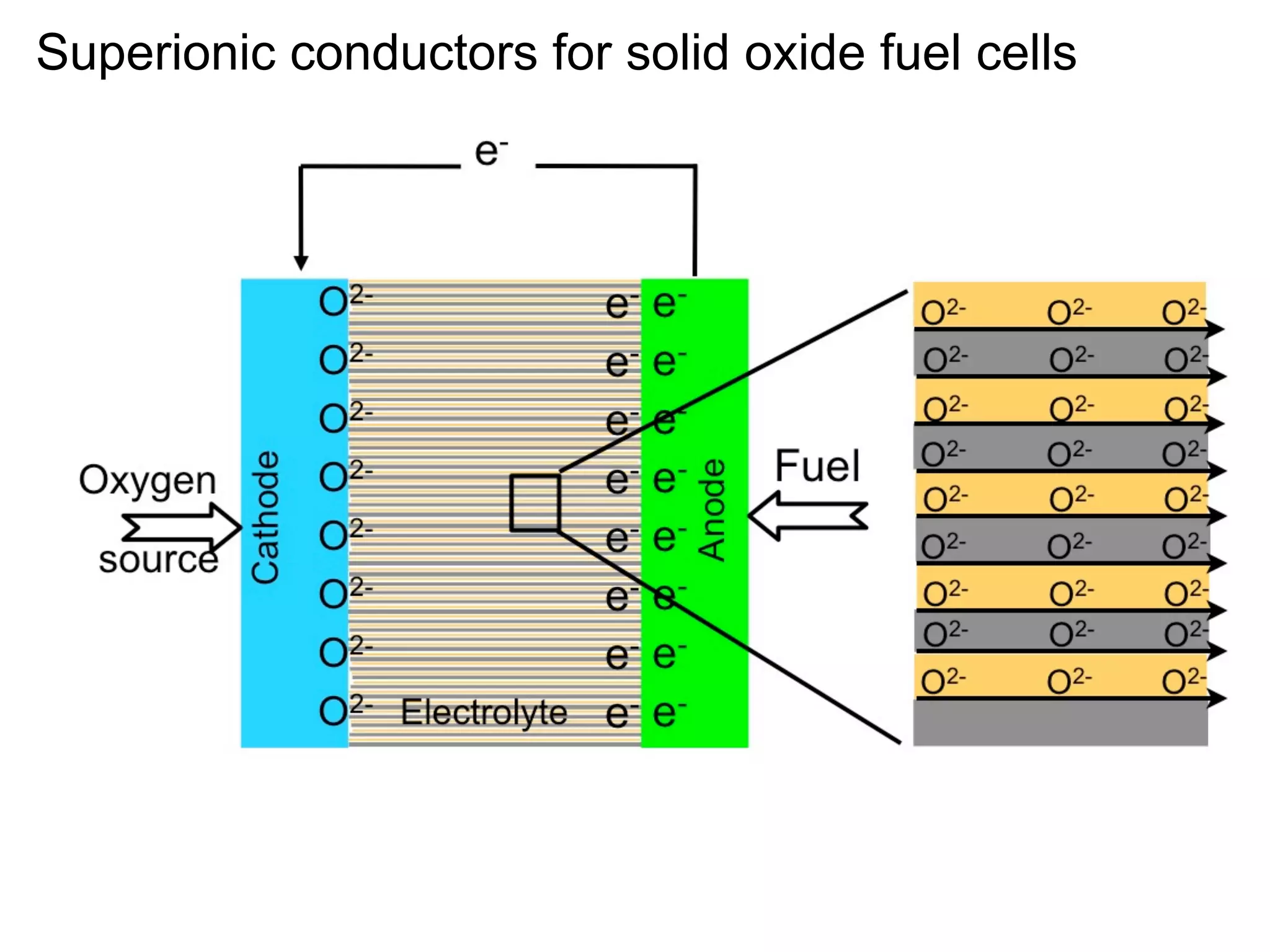
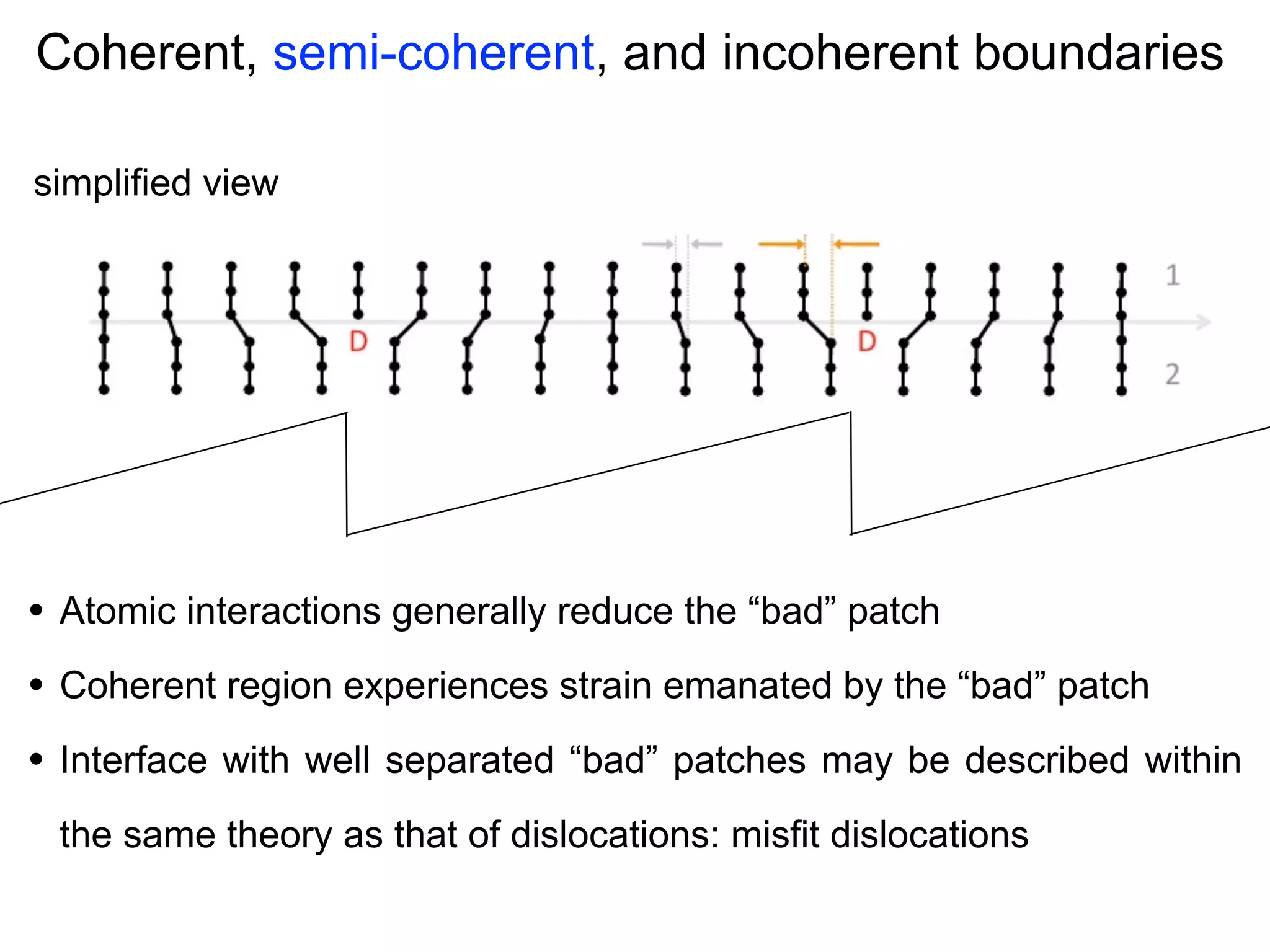
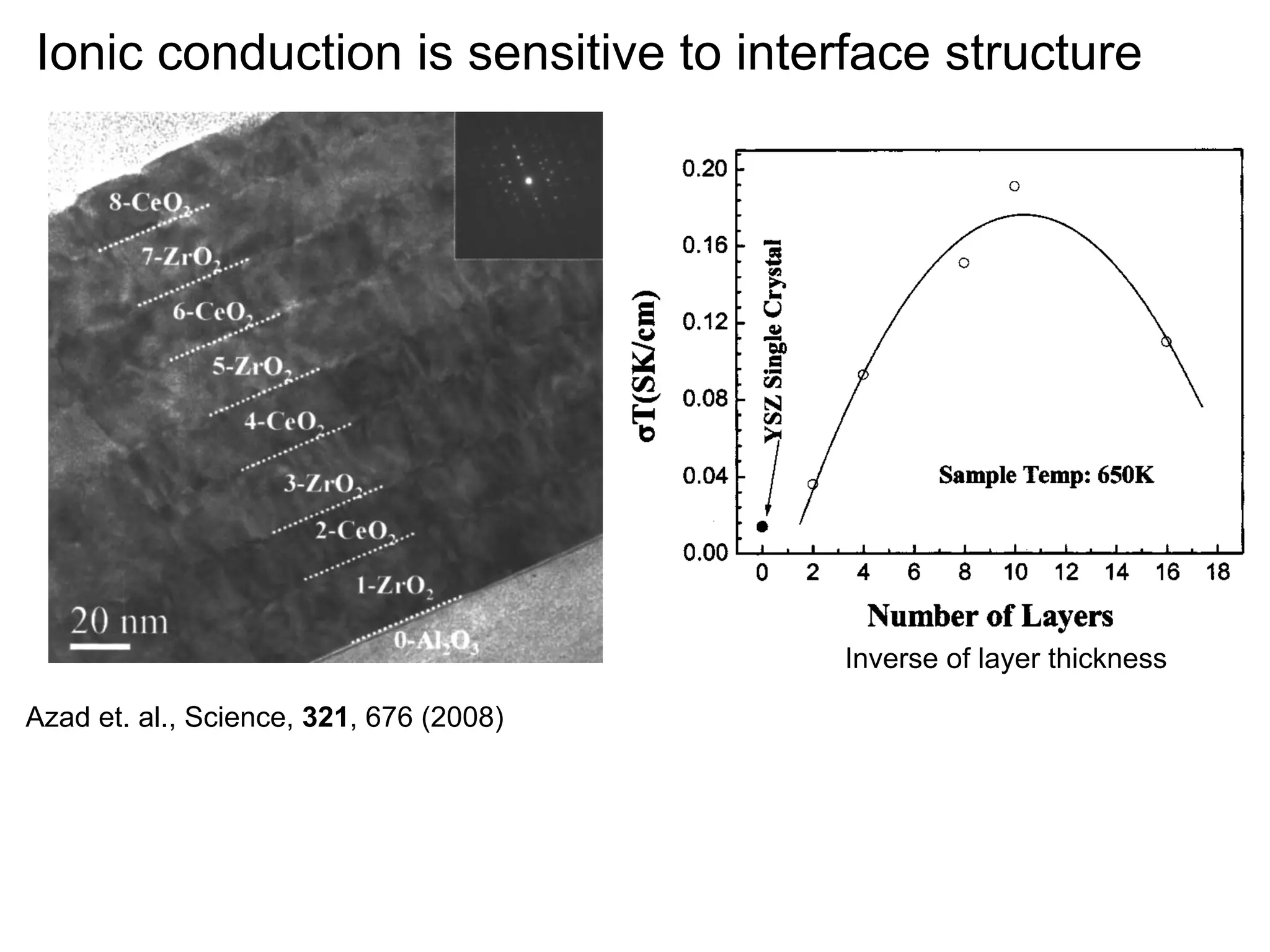
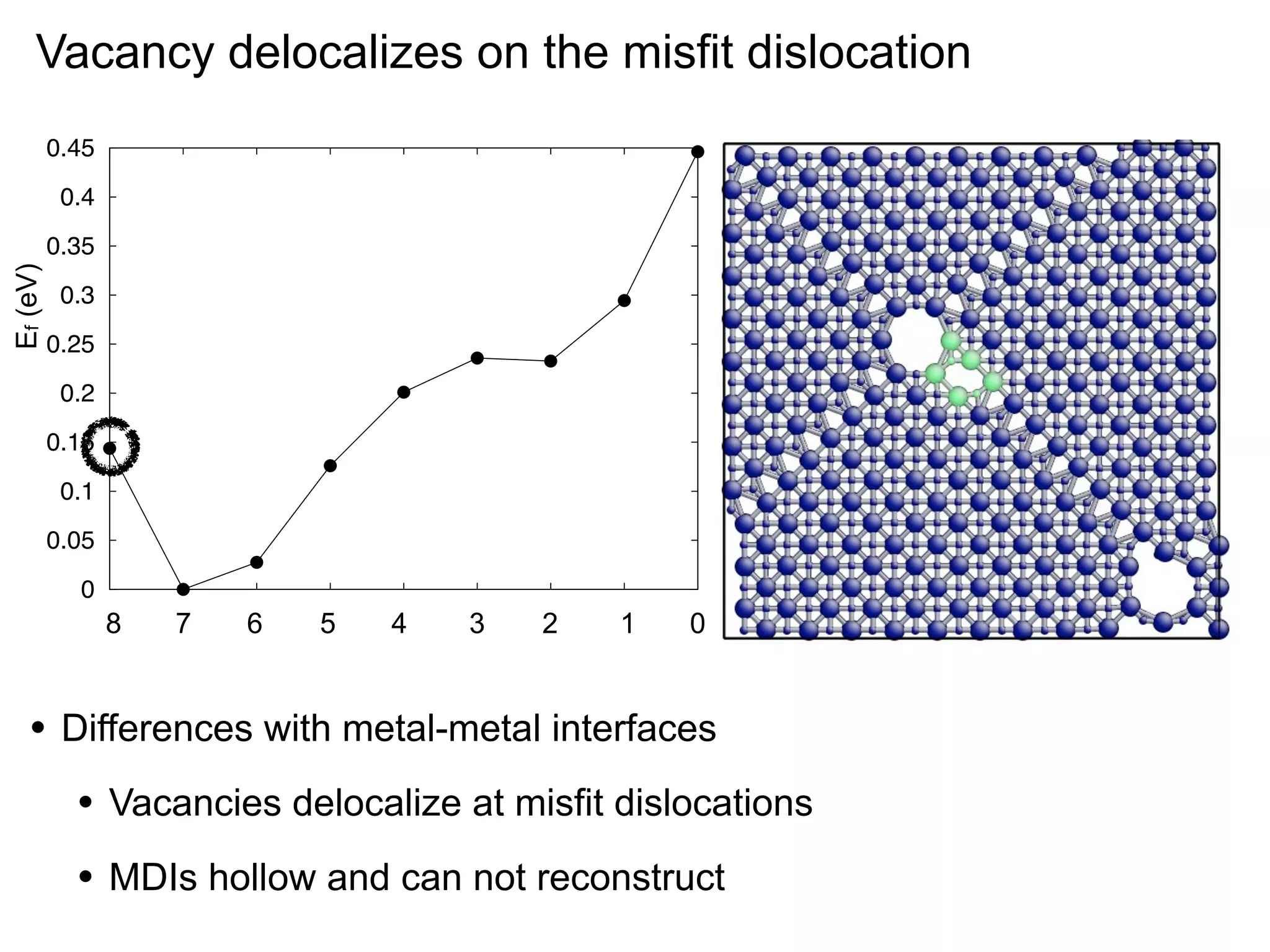
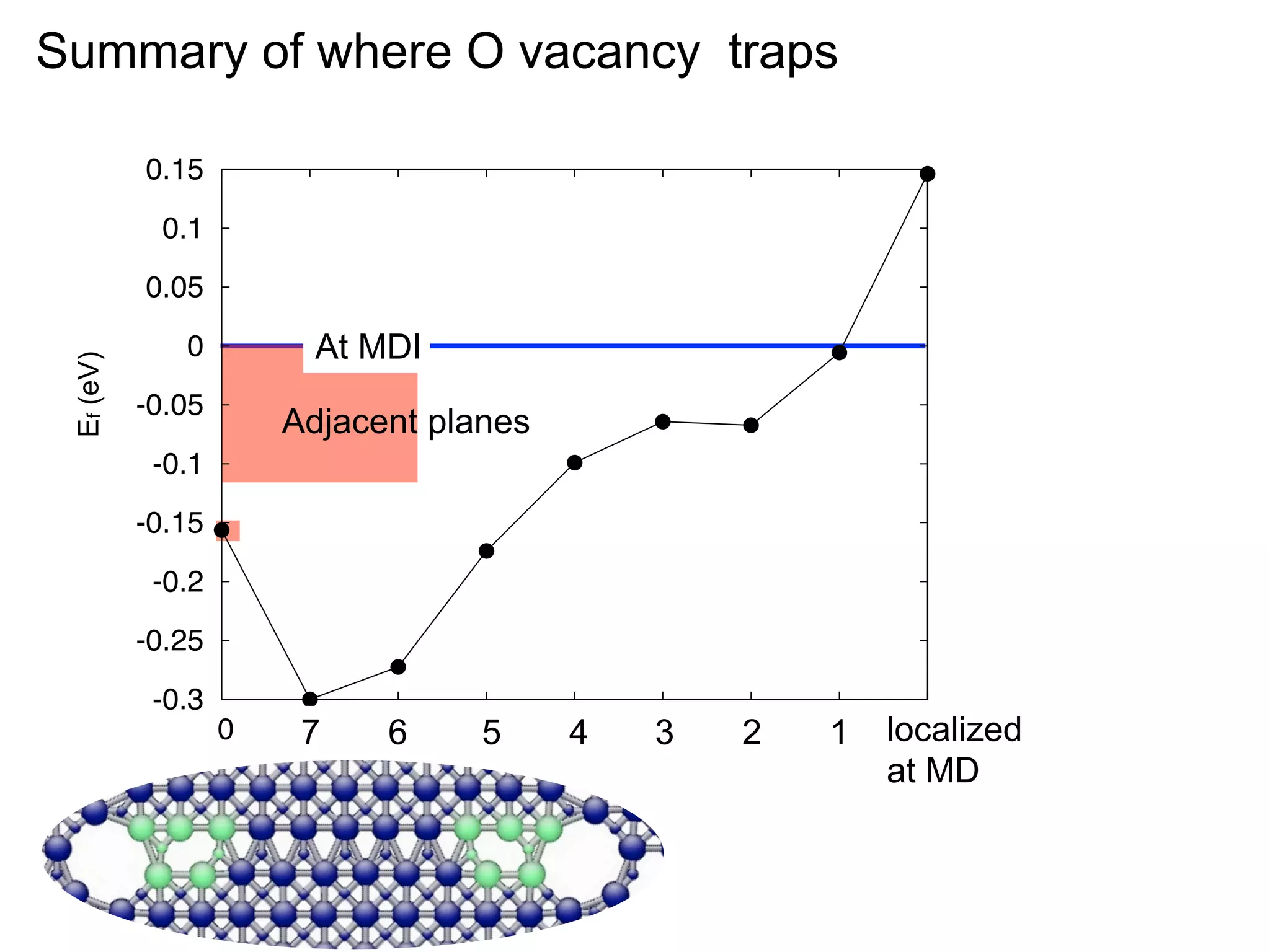
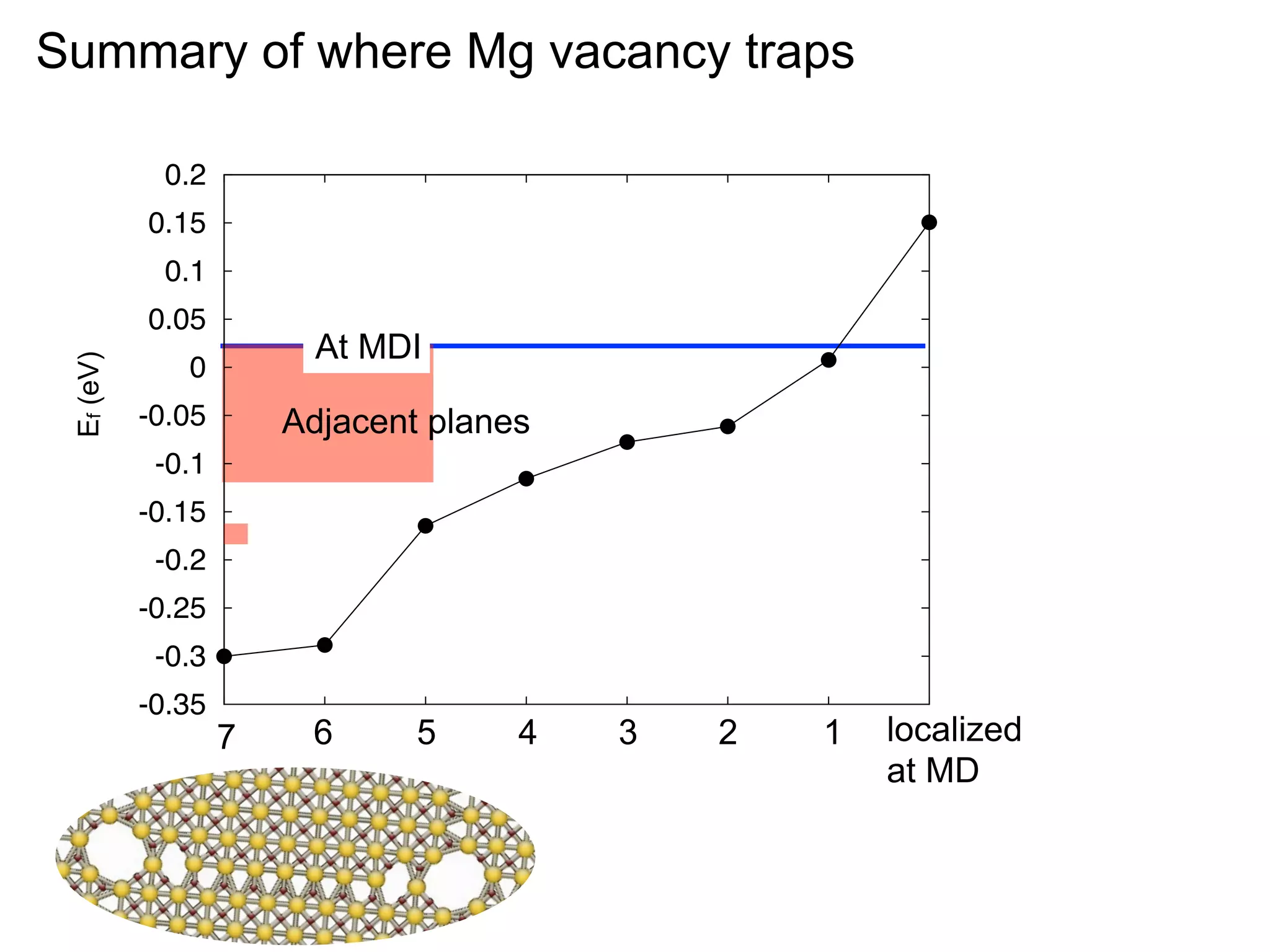
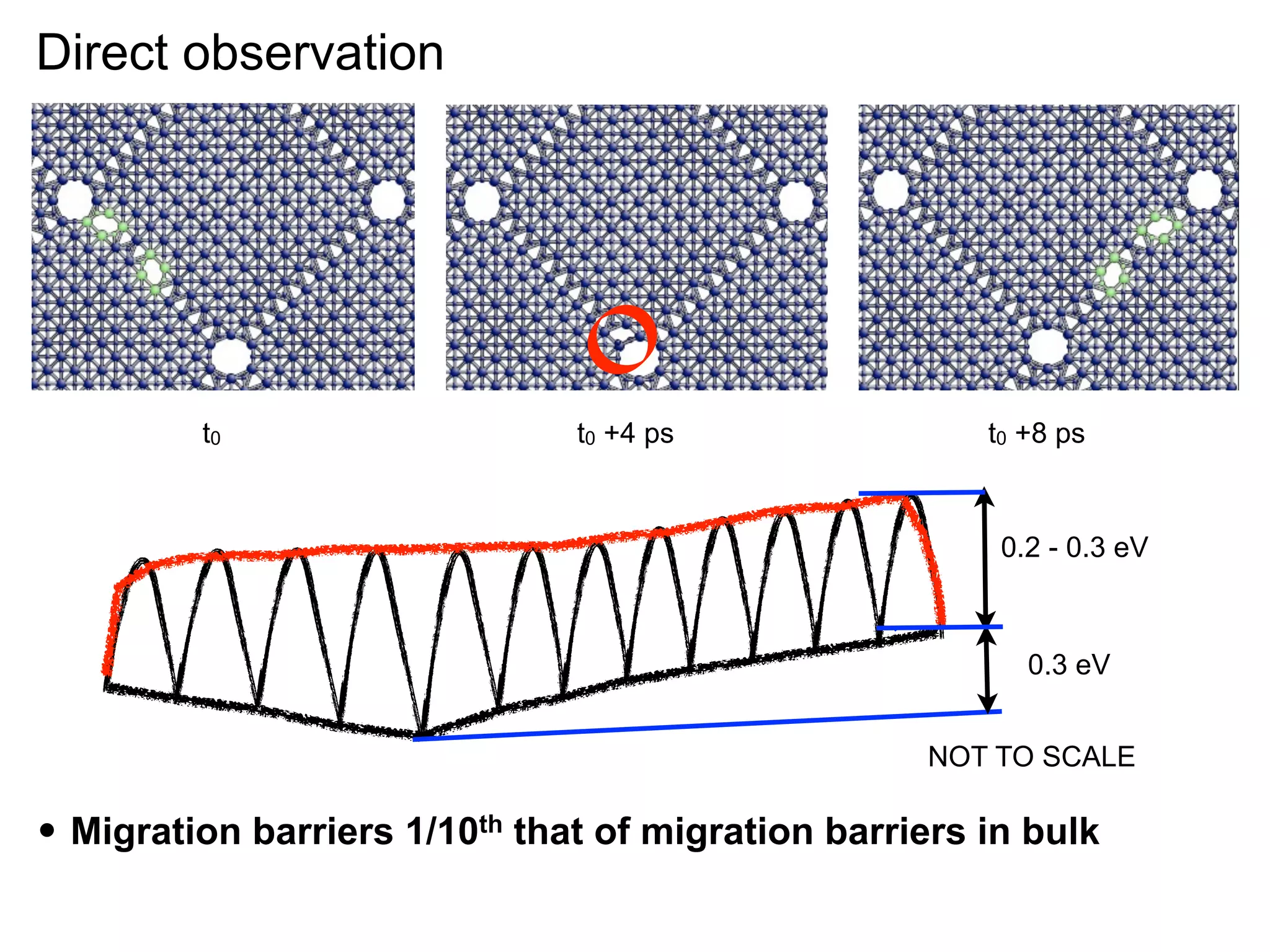
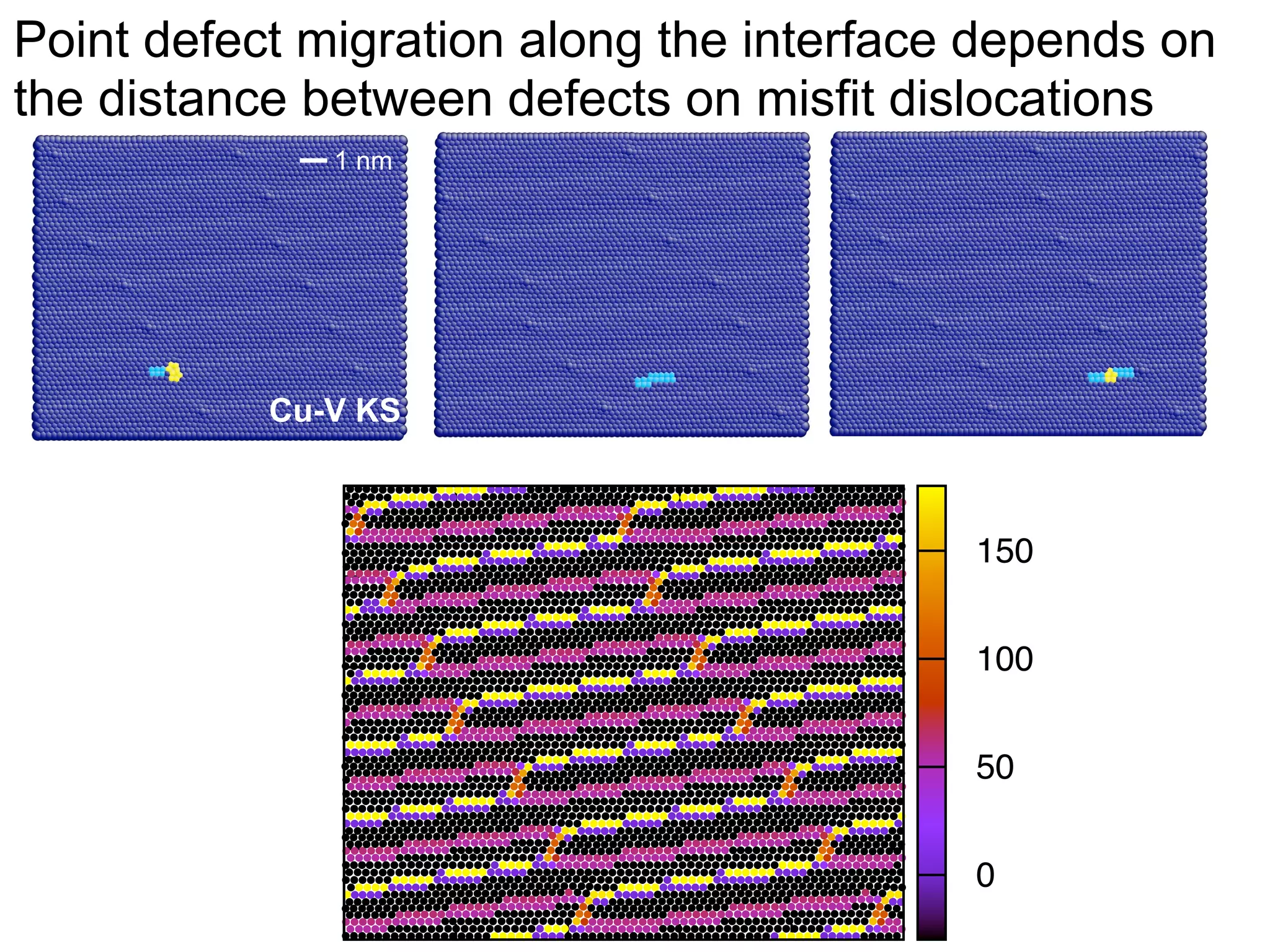
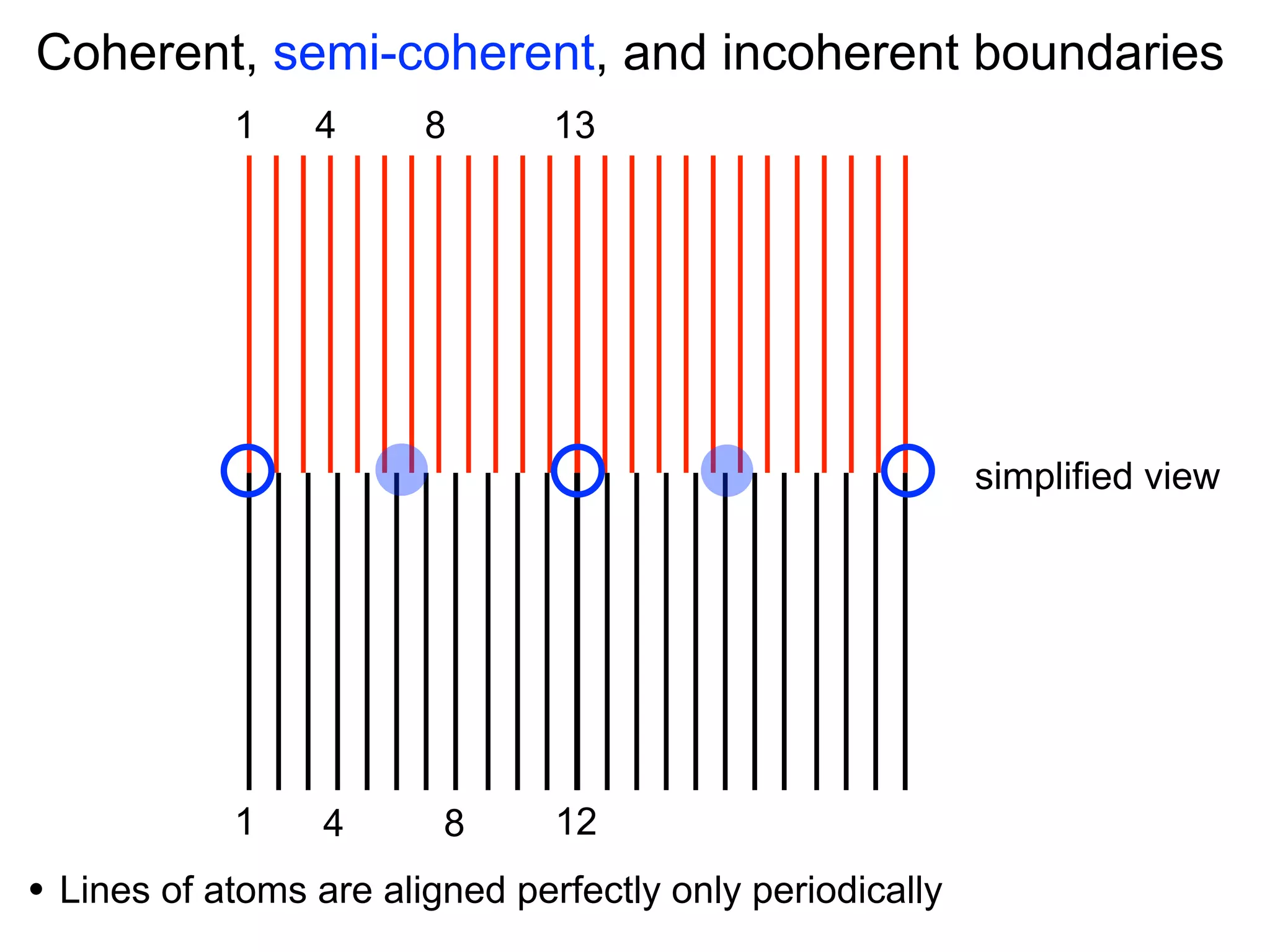
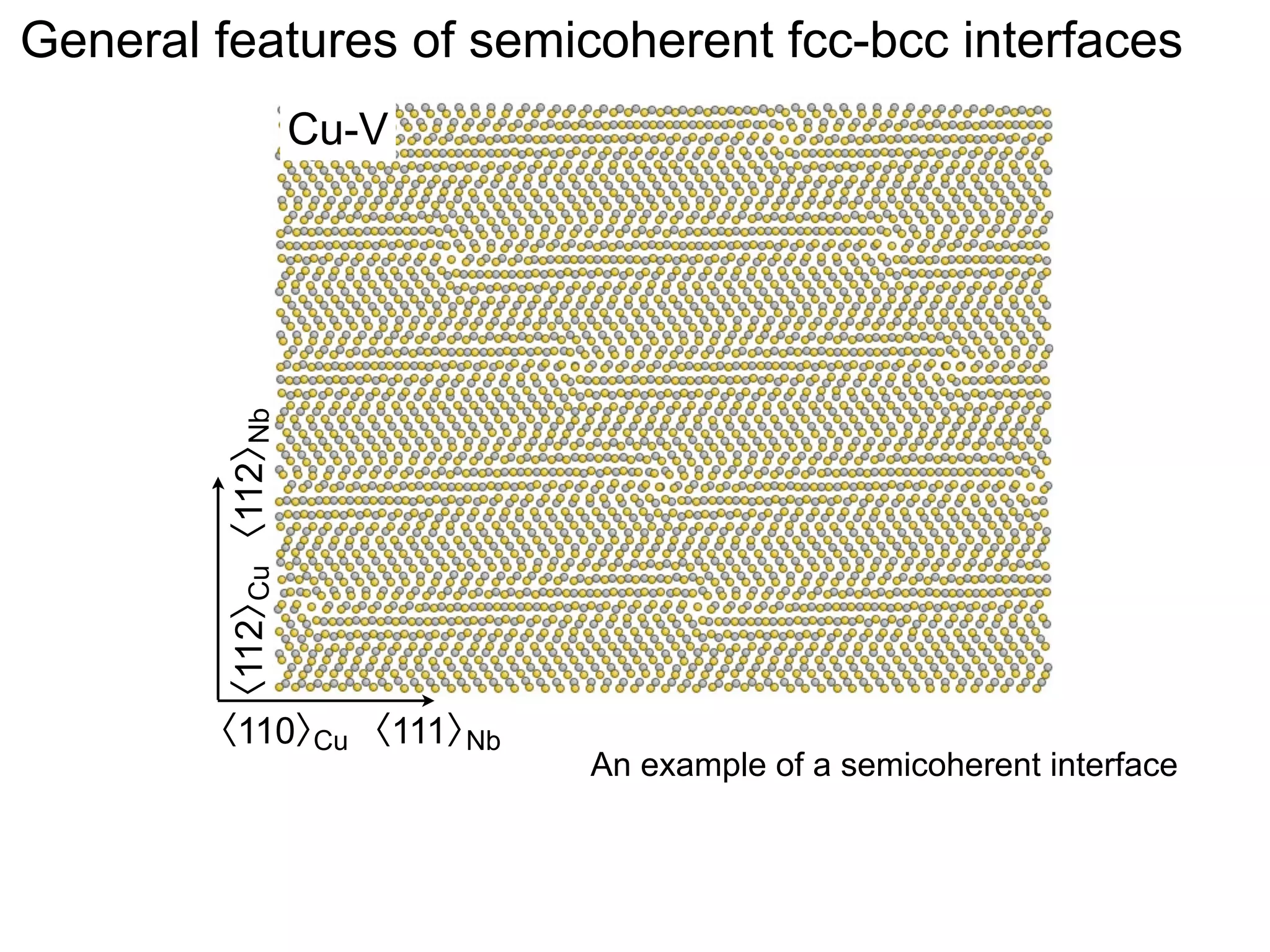
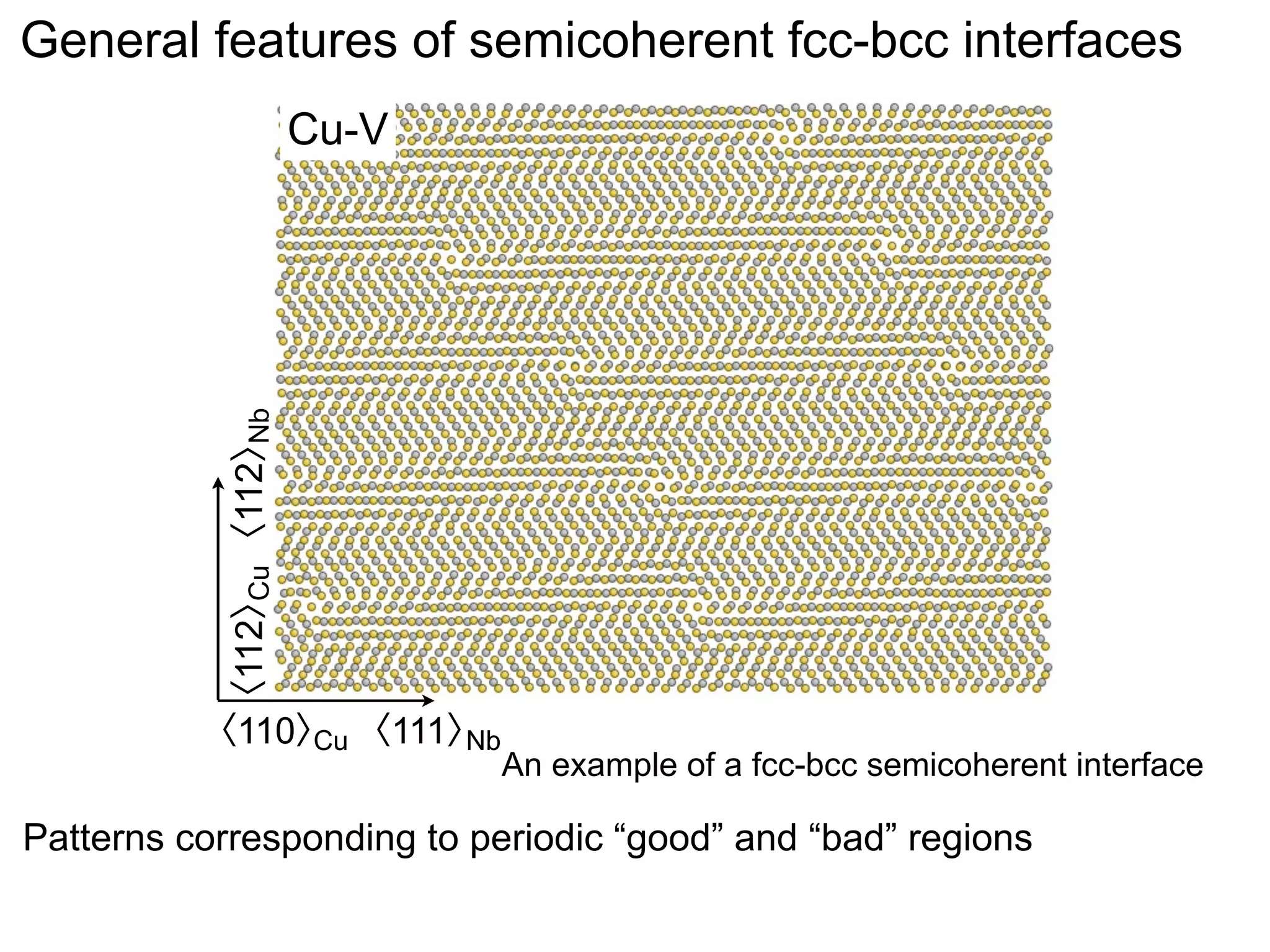
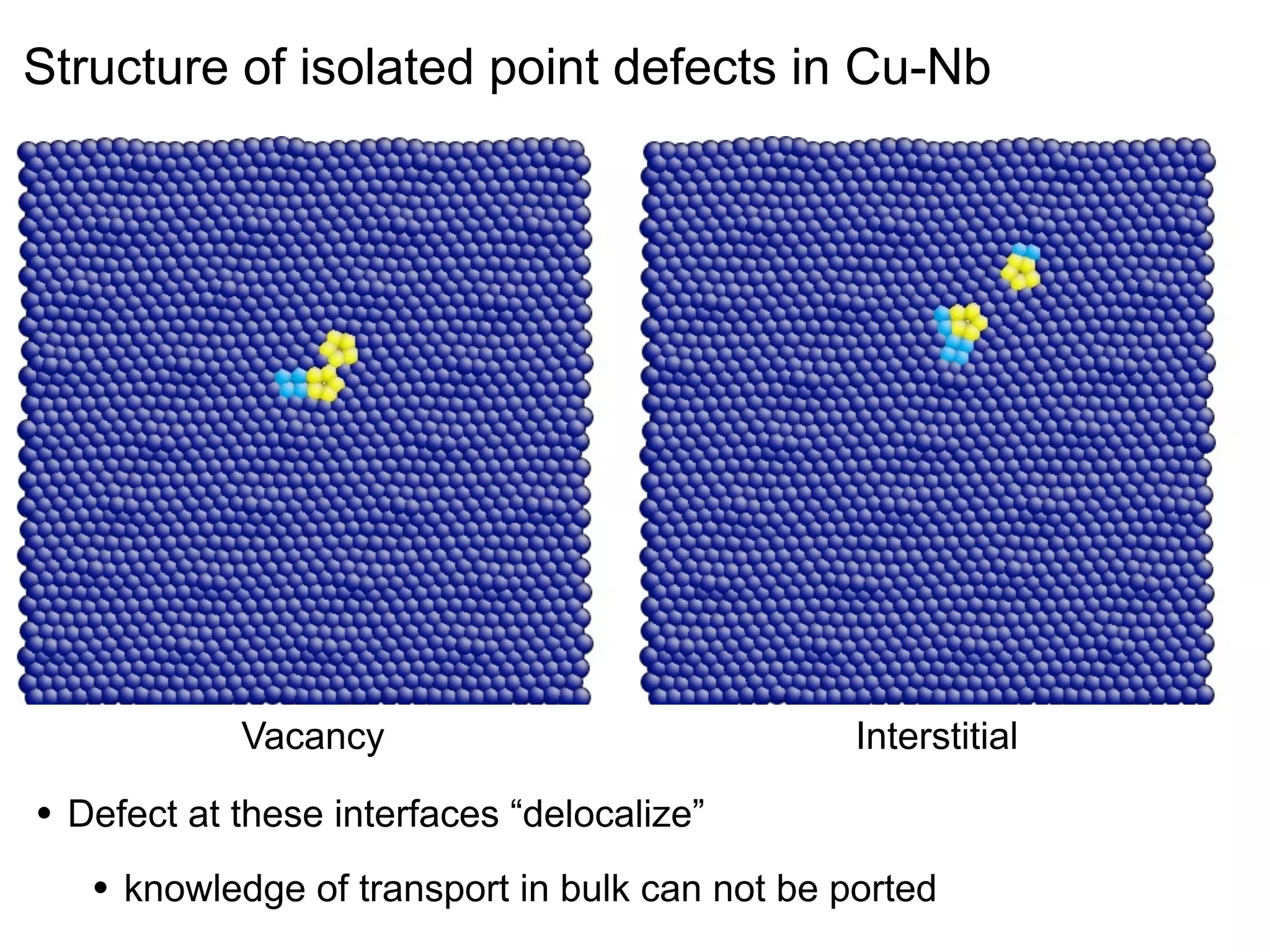
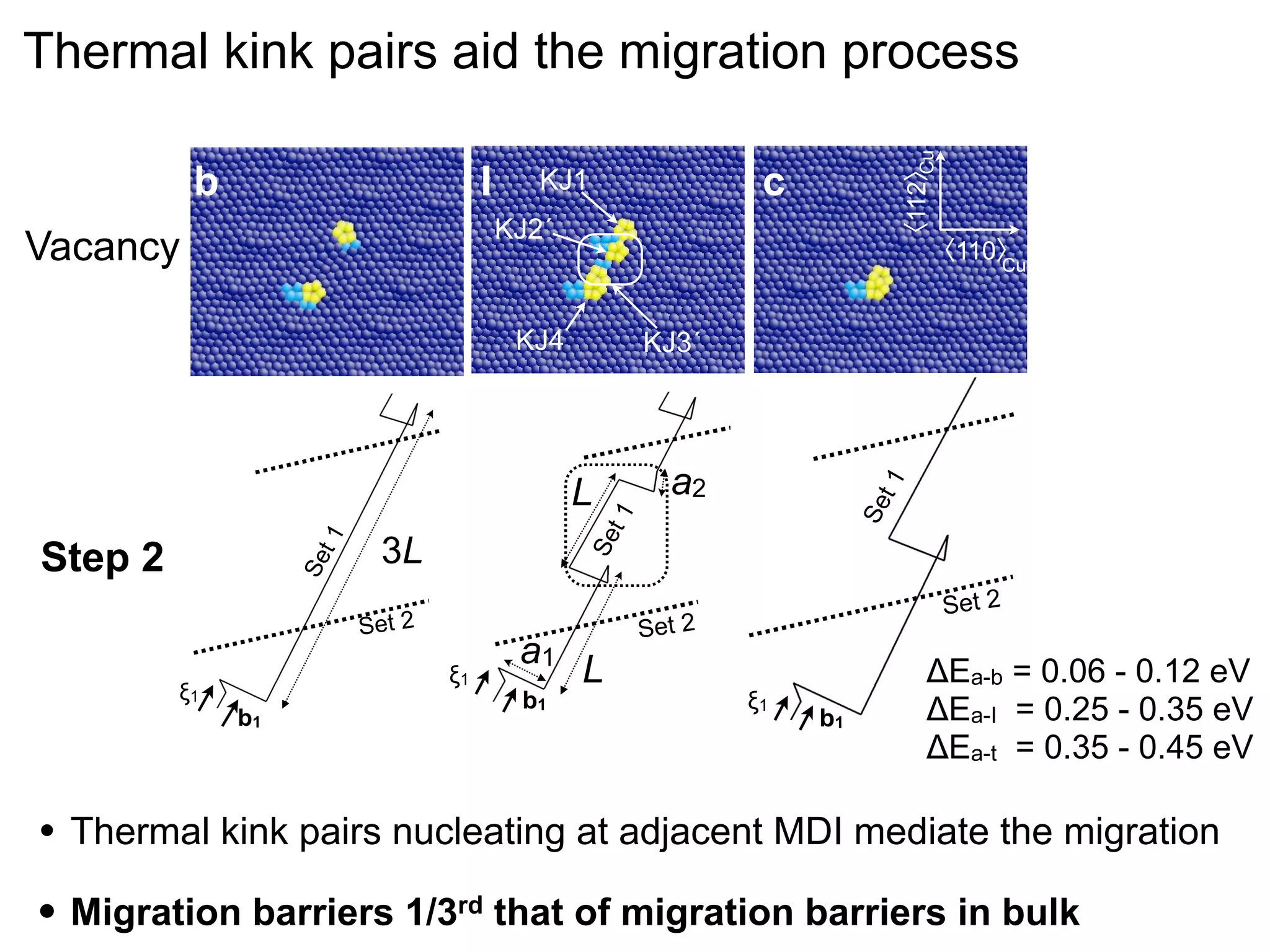
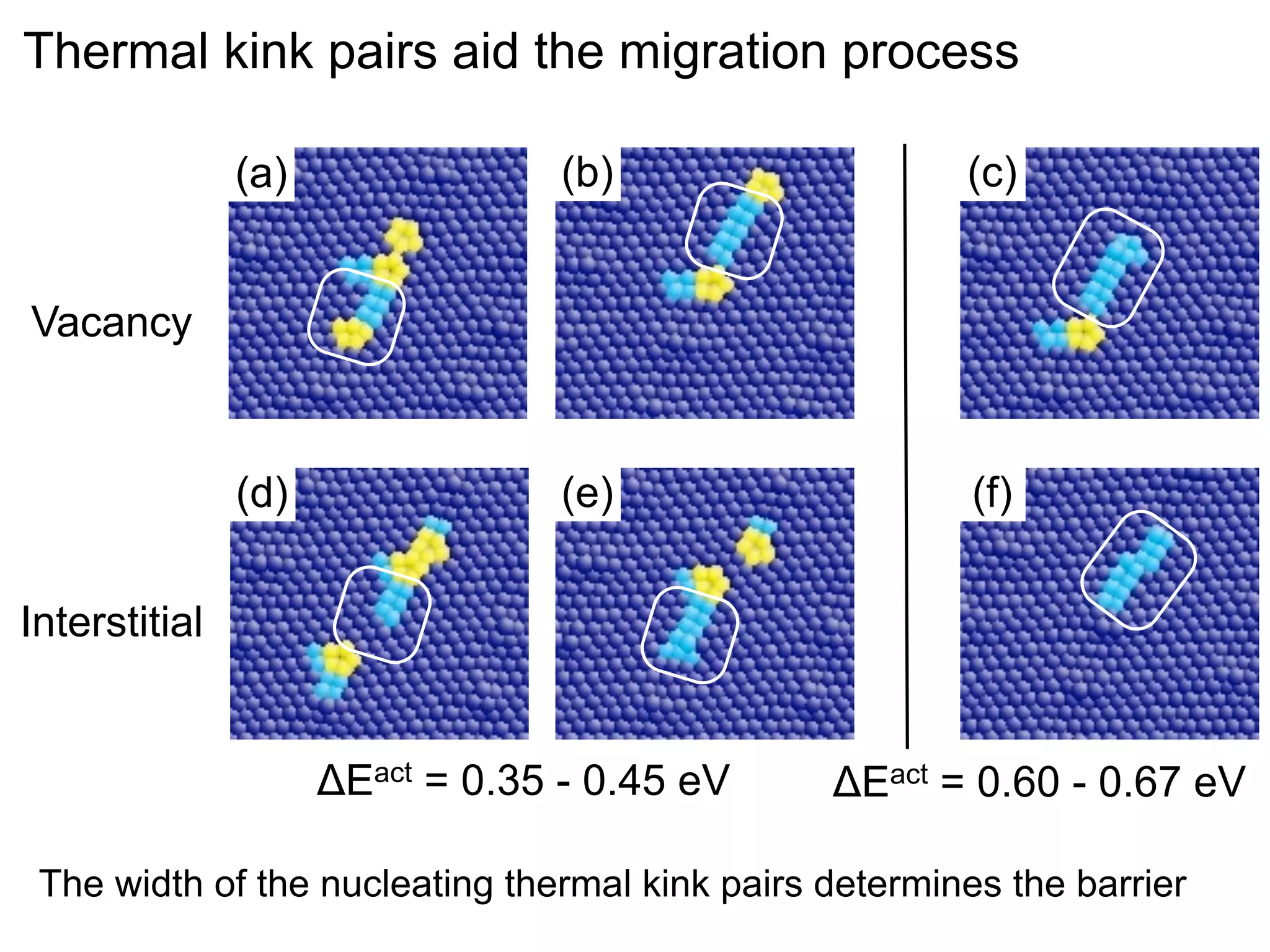
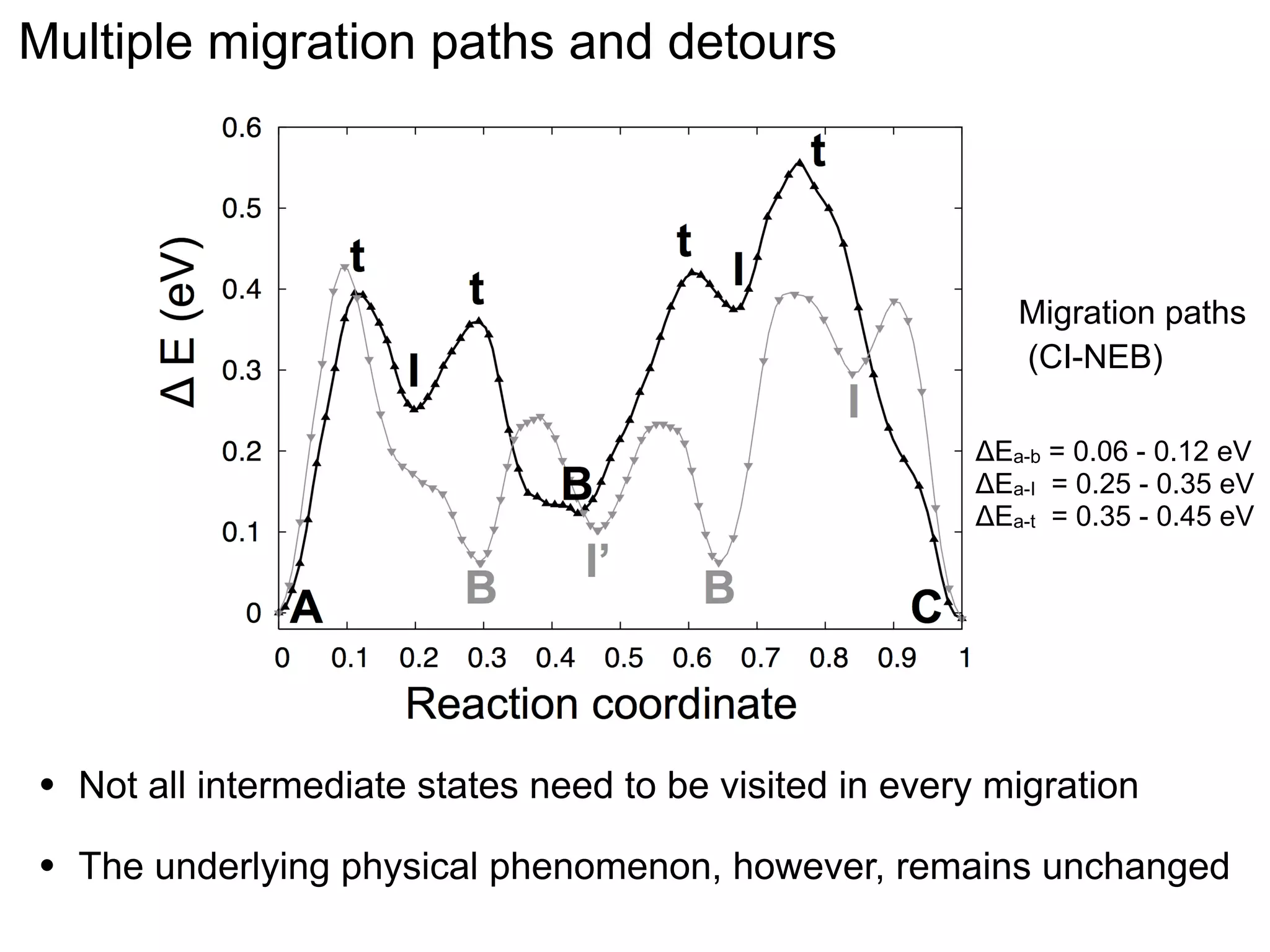
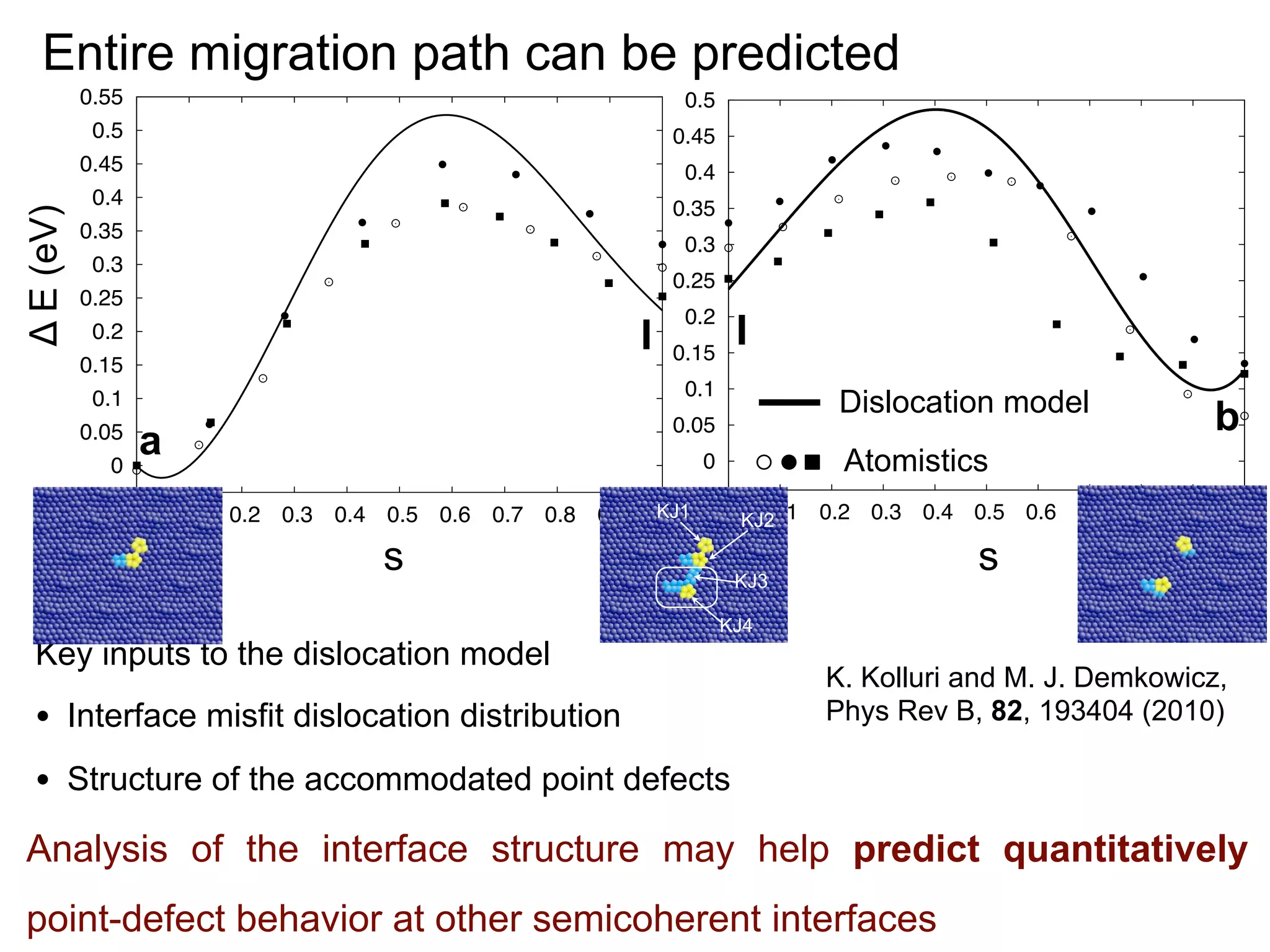
Mass transport at internal interfaces of inorganic materials - Ionic conduction is sensitive to interface structure, with interfaces enhancing ionic conduction due to high defect concentrations, strain-enhanced diffusion, and interface-modified structure (1-2 sentences) - Point defects at semicoherent metal interfaces like Cu-Nb delocalize across the interface and migrate between misfit dislocation arrays, with the lowest barrier for vacancy migration between 0.06-0.12 eV (1 sentence) - 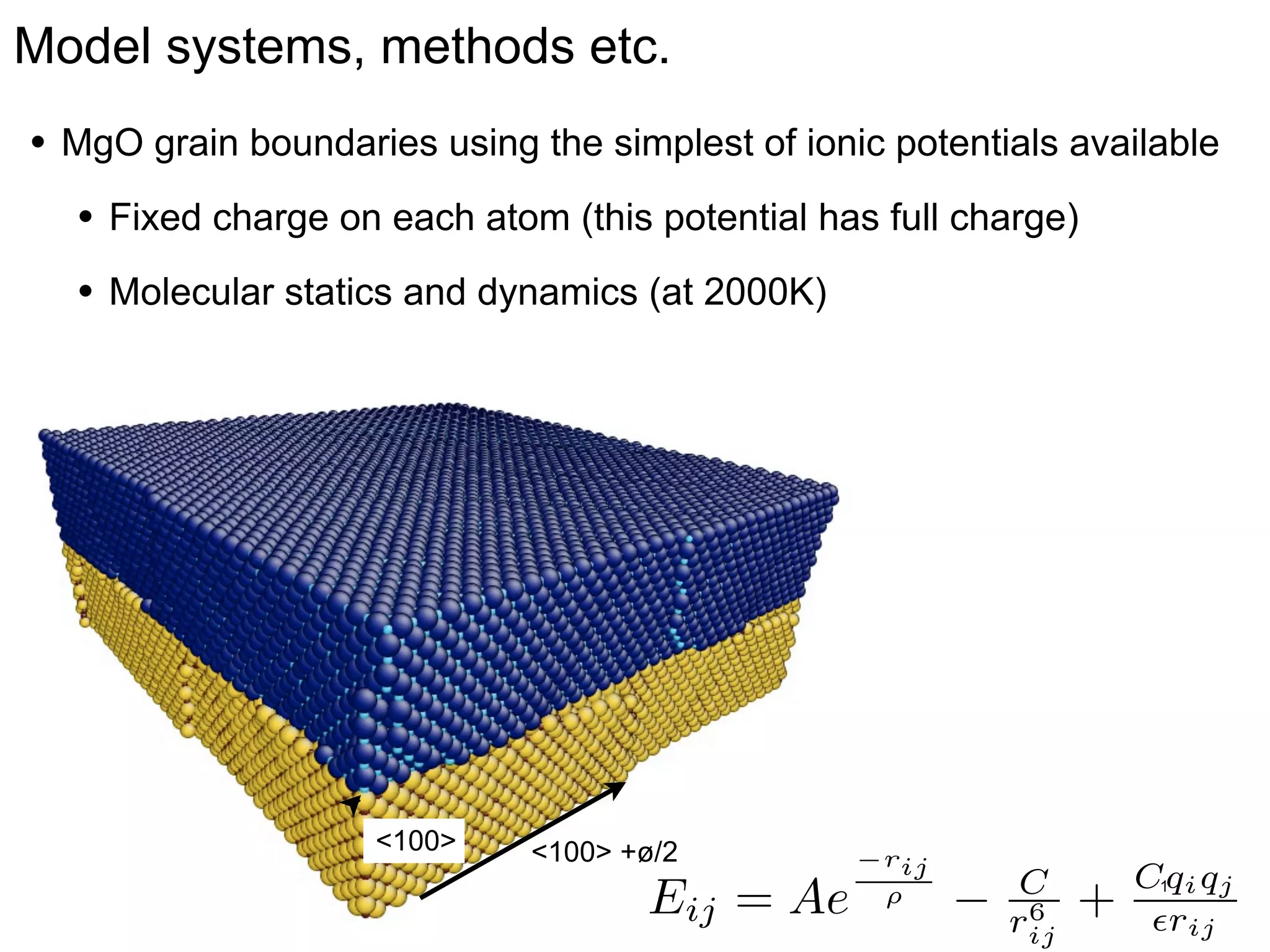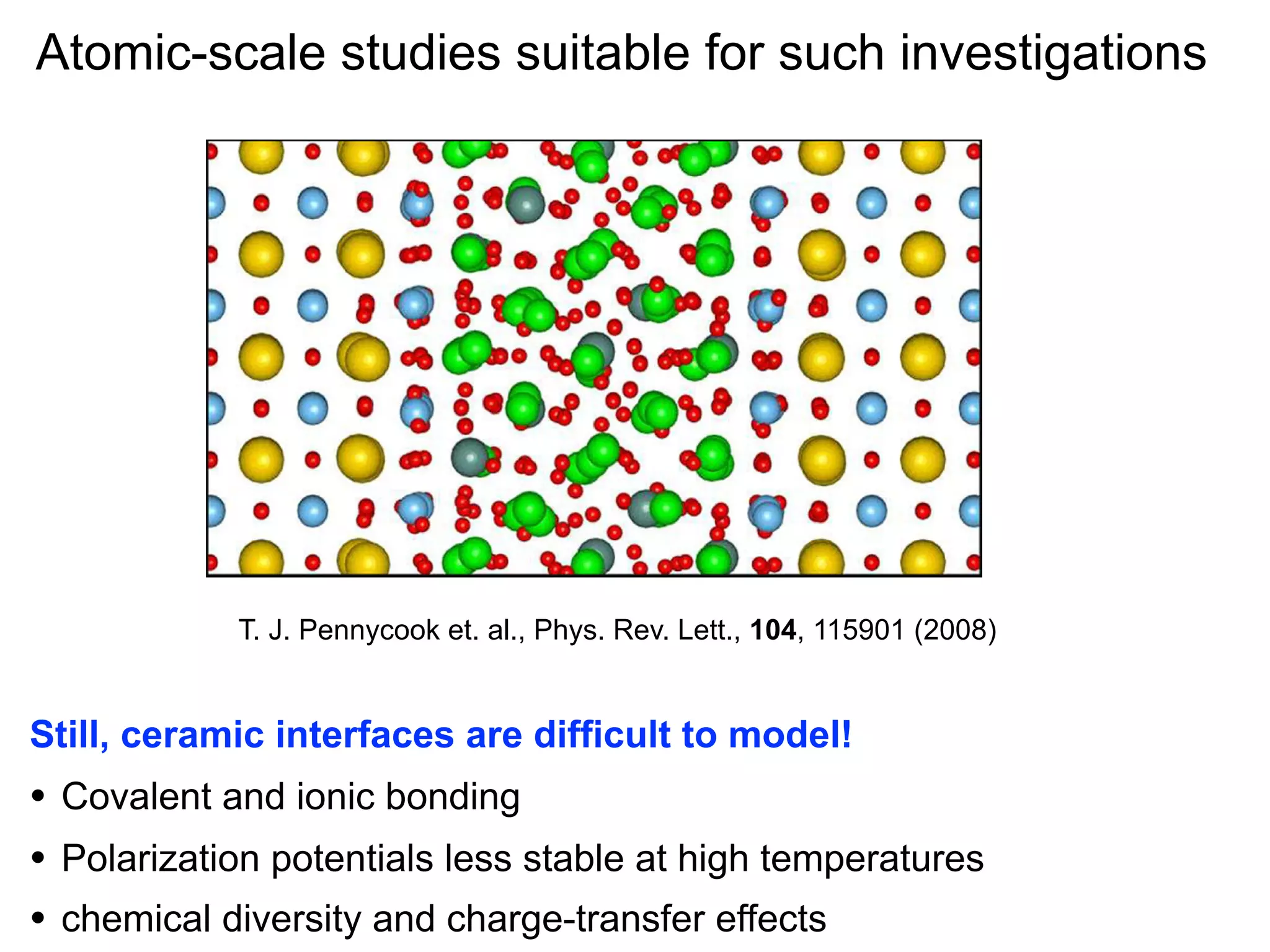Understanding defect behavior at metal interfaces provides insights into modifying ion transport at ceramic interfaces like grain boundaries in materials like MgO (1 sentence)

1. Mass transport at internal interfaces of
inorganic materials
Kedarnath Kolluri, M. J. Demkowicz and B. Uberuaga
Acknowledgments:
R. G. Hoagland, J. P. Hirth, A. Kashinath, A. Vattré, X.-Y. Liu, A. Misra, and A. Caro
Financial Support:
Center for Materials at Irradiation and Mechanical Extremes (CMIME) at LANL,
an Energy Frontier Research Center (EFRC) funded by
U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences

2. Internal interfaces enhance ionic conduction
•
•
•
Downloaded from www.sciencemag.org on September 17, 2011
byand with the thickness of the lattice.shows that the large degraded interface structure when the YSZ layers
strains to match the STO YSZ, Because the frequency plots. In the presence of blocking effects
exceed the critical electrodes,
conductivity values in these heterostructures due
inbulk lattice constants of STO and YSZ are orig- to grain boundaries orthickness. a further
ee
ues Fig. 3. Dependence of the logarithm of the
in long-range ionic conductivity of the trilayers
his STO/YSZ/STO versus inverse temperature. The
to thickness range of the YSZ layer is 1 to 62 nm.
gi- Also included are the data of a single crystal
0.6
is (sc) of YSZ and a thin film (tf) 700 nm thick
1
[taken from (7)] with the same nominal
he composition. (Top inset) 400 K conductance
is of [YSZ1nm/STO10nm](ni/2) superlattices as a
gle function of the number of interfaces, ni.
eas (Bottom inset) Dependence of the conductgle ance of [STO10nm/YSZXnm/STO10nm] trilayers at
1.1
ior 500 K on YSZ layer thickness. Error bars are
ers according to a 1 nS uncertainty of the con1
ductance measurement.
ler
yer
outFig. 1. (A) Z-contrast scanning transmission electron microscopy (STEM) image of the STO/YSZ interface of
J. Garcia-Barriocanal et. al., Science, 321, 676 (2008)
dcthe [YSZ1nm/STO10nm]9 superlattice (with nine repeats), obtained in the VG Microscopes HB603U
sesmicroscope. A yellow arrow marks the position of the YSZ layer. (Inset) Low-magnification image obtained
Why?
in the VG Microscopes HB501UX column. In both cases a white arrow indicates the growth direction. (B) EEL
he
sesspectra showing the O K edge obtained from the STO unit cell at the interface plane (red circles) and 4.5 nm
High defect concentrations
into the STO layer (black squares). (Inset) Ti L2,3 edges for the same positions, same color code. All spectra
vaare the result of averaging four individual spectra at these positions, with an acquisition time of 3 s each.
of Faster transport due to interface structure; Strain-enhanced diffusion
areFig. 2. Real part of the lateral
No conductivity versus freorselectrical space charge in this example but possible in other interfaces

3. Superionic conductors for solid oxide fuel cells

4. Superionic conductors for solid oxide fuel cells

5. ystal substrates were ultrasonically cleaned in ac-
Ionic conduction is sensitive to interface structure
131906-3
Azad et al.
Inverse of layer thickness
FIG. 4. Conductivities of single crystal YSZ ͑Ref. 14͒, two-, four-, e
M Azad et. al., Science, a cross sectional view of an eight-layer
micrograph showing 321, 676 (2008) ten-, and sixteen-layer films at 650 K.
ed CeO2 and ZrO2 film grown on Al2O3͑0001͒.
was measured as a function of temperature using a f
probe van der Pauw technique.12 Since the electronic
© 2005 American Institute of Physics
ductivity in these oxides is significantly less compare
ht; see http://apl.aip.org/about/rights_and_permissions
ionic conductivity, especially at low temperatures, ionic
13

6. week ending
Atomic-scale T E R S suitable for such investigations
studies
REVIEW LET
19 MARCH 2010
T. J. Pennycook
al., Phys. of Lett., nm YSZ (2008)
FIG. 3 (color online). et. StructureRev. the 1104, 115901layer sandwiched between layers of STO at 360 K. Sr atoms are shown as
Still, large yellow balls, Ti in are difficult to model! and O in red.
ceramic interfaces blue, Zr in green, Y in gray,
• Covalent and ionic bonding
ime
of a large uncertainty in the density and the fact that
• Polarization potentials less stable at high temperatures the
set)
charge on the ions is ill-defined. We can, however, estimate
near chemical diversity and charge-transfer effects ratio of the
•
the effective magnitude by evaluating the

7. The Radiation Damage Tole
Perhaps we could start Ultra-High Strength Nan
of with metals!
Composites
• Good interatomic potentials exist for metallic systems
•
•
A. Misra, M.J. Demkowicz, X. Zhang, mass Hoagland
less difficult - can probe the effect of structure on and R.G. transport
interfaces are to act as sinks for radiaInterfaces act as obstacles to slip
tion-induced defects. Studies conducted
and sinks for radiation-induced defects.
on sputter-deposited Cu-Nb multilayers
Hence, nanolayered composites that
contain a large volume fraction of interfaces provide over an order of magnitude
After He implantation
increase in strength and enhanced radiation damage tolerance compared to bulk
materials. This paper shows the experimental and atomistic modeling results
|| (110)
and
〈111〉
(111)
from
Kurdjumov-Sachs (KS): a Cu-Nb nanolayered composite 〈110〉 ||
fcc
bcc
fcc
bcc
to highlight the roles of nanostructuring length (111) and || response of
scales
the
〈100〉
Nishiyama-Wassermann (NW): to ion collision(110)bcc and〈110〉 ||
interfaces
fcc cascades in
fcc
bcc
150 keV He, 1017 cm-2, 300 K
a
designing composite materials with high
radiation damage tolerance.
Initial focus on
•
interfaces of immiscible fcc-bcc semicoherent metal systems
Cu-Nb, Cu-V, Cu-Mo, Cu-Fe, and Ag-V
INTRODUCTION
The performance of materials in
Motivated by experiments
extreme environments of irradiation
and temperature must be significantly
improved to extend the reliability, lifetime, and efficiency of future nuclear
reactors. 1 In reactor environments,
b
damage introduced in the form of radia- A. Misra et al., JOM, Sept, 62 (2007)

8. Outline
•
Structure and properties of semicoherent interfaces
•
Point defects at semicoherent interfaces
•
Migration of point defects and relation to the interface structure
•
Implications to ceramic interfaces
•
case of MgO grain boundaries

9. Coherent, semi-coherent, and incoherent boundaries
simplified view
•
Lower and upper grains are in “perfect” alignment always

10. Coherent, semi-coherent, and incoherent boundaries
1
4
8
13
simplified view
1
•
4
8
12
Lines of atoms are aligned perfectly only periodically

11. Coherent, semi-coherent, and incoherent boundaries
simplified view
•
Atomic interactions generally reduce the “bad” patch
•
Coherent region experiences strain emanated by the “bad” patch
•
Interface with well separated “bad” patches may be described within
the same theory as that of dislocations: misfit dislocations

12. General features of semicoherent fcc-bcc interfaces
〈112〉 〈112〉
Cu
Nb
Cu-V
〈110〉 〈111〉
Cu
Nb
An example of a semicoherent interface

13. View of the Interface

14. View of the Interface

15. View of the Interface

16. View of the Interface

17. View of the Interface

18. View of the Interface

19. General features of semicoherent fcc-bcc interfaces
〈112〉 〈112〉
Cu
Nb
Cu-V
〈110〉 〈111〉
Cu
Nb
An example of a fcc-bcc semicoherent interface
Patterns corresponding to periodic “good” and “bad” regions

20. General features of semicoherent fcc-bcc interfaces
〈112〉 〈112〉
Cu
Nb
Cu-V
〈110〉 〈111〉
Cu
Nb
Interface contains arrays of misfit dislocations separating coherent
regions

21. 〈112〉 〈112〉
Cu
Nb
General features of semicoherent fcc-bcc interfaces
Cu-Nb
〈110〉 〈111〉
Cu
Nb
Cu-V
Interface contains arrays of misfit dislocations separating coherent
regions

22. MDI
1 nm
〈112〉
Cu
General features of semicoherent fcc-bcc interfaces
Cu-Nb KS 〈110〉
Cu
Cu-V KS
•
Two sets of misfit dislocations with Burgers vectors
•
Misfit dislocation intersections (MDI) where different sets of
dislocations meet

23. Outline
•
Structure and properties of semicoherent interfaces
•
Point defects at semicoherent interfaces
•
Migration of point defects and relation to the interface structure
•
Implications to ceramic interfaces
•
case of MgO grain boundaries

24. 0 0
00
Defects on misfit dislocations are good traps to point
defects
150
150
0.2
0.2
0.4
0.4
100
100
0.6
0.6
50
50
0.8
0.8
0
0
1
10
0
0.2
0.2
0.4
0.4
0.6
0.6
Cu-Nb KS
Cu-Nb KS
0.8
0.8
1
1
0.28
0.28
0.26
150 0.45
1500.26
0.24
150
0.2 0.2
0.2
150
0.2 0.45
0.24
0.2 0.2
0.2
0.2
0.22
0.4
0.22
0.4
0.2
100
1000.2
0.4 0.4
0.4 0.35 0.4
100
100
0.4 0.4
0.18
0.4 0.35 0.4
0.18
0.16
0.3 0.6
0.6 0.6
0.6 0.3
50
50 0.16
0.14
0.6 0.6
0.6
0.6
50
50
0.14
0.25
0.12
0.8 0.8
0.8
0.8 0.25
0.1 0.12
0 0.8
0 0.1
0.8 0.8
0.8
0.2
0.08
0
0
0.2
1
0.060.08
1 0.15 1
1
0
0.2 0.2
0.4 0.4
0.6 0.6
0.8 0.8
1
0
0.2
0.8
1
1
0.06
1 0.15 0.2
0
1
0
0.4 0.4 0.6 0.8
0.6
11
1
0
0.2 0.2
0.4 0.4
0.6 0.6
0.8 0.8
1
0
0.2
0.4
0.6 0.8
0.8
0
1
0
0.2
0.4
0.6
11
0
0
0
0 0.5
0
0 0.5
0
0
Angle with -ve x axis
Angle with -ve x axis
0
0
0
Cu-Fe NW
Cu-Fe NW
0.2
0.4
0.6
0.8
Cu-V KS
Cu-V KS
0
0
0
0.2
1.2
0.4
0.6
1
0.6
0.8
1.2
0.6
0.8
0
0.2
0.4
0
0.2
1 nm 0.4
1 nm
0.6
0.6
0.8
0.8
0.6
1
1
1.4
0.2
1.2
1.2
0.4
1.2
0.4
1
1
1
1
0.6
0.6
0.8
0.6
0.8
0.6
0.8
0.8
0.8 0.8
0.8
1
0.2
0.4
1
1.4
1.4
0.2
1.2 0.4
0.4
0
1.4
1.4 0.2
0.2
1
0
0
1.4
0.8
1
0.6
0
1
1
0
1
0.8
0.6
0.6
0.8
0.2
0
0.4
10.2 0.4
nm
1 nm
0.6
0.6
0.8
0.8
1
1
Formation energy (eV)
Formation energy (eV)
Different fcc-bcc semicoherent interfaces with misfit dislocations
0.2
0
0.4
0.2
1.4 nm 0.4
1.4 nm
0.6
0.8
0.6
0.6
1
0.8
1
Vacancy formation energies (similar trend for interstitials as well)
1
0
0.2
0.4
0.6
0.8
01
0
0

25. Structure of isolated point defects in Cu-Nb
Vacancy
•
Interstitial
Defect at these interfaces “delocalize”
•
knowledge of transport in bulk can not be ported

26. Outline
•
Structure and properties of semicoherent interfaces
•
Point defects at semicoherent interfaces
•
Migration of point defects and relation to the interface structure
•
Implications to ceramic interfaces
•
case of MgO grain boundaries

27. Point defects migrate from one MDI to another in CuNb
Vacancy
Interstitial
•
Migration is along set of dislocation that is predominantly screw
•
In the intermediate step, the point defect is delocalized on two MDI

28. 0.45
0.4
Vacancy
I
KJ1t
t
Se
KJ3
!1
b1
•
t
KJ3´
a2
0.15
0.1
a1 L
!1
0.05
b1
b
t1
L
t1
L
0.2
t
t
I
I
0 a
•
KJ4
〈110〉
Cu
KJ4
0.25
Set 2
〈110〉
Cu
Se
t1
Step 1
t
Se
" E (eV)
a2 a1
KJ1
KJ2´
0.35
0.3
b
KJ2
〈112〉
Cu
a
〈112〉
Cu
Isolated point defects in CuNb migrate from
one MDI to another
Set 2
3L
Set 2
!1
b1
b
Interstitial
Vacancy
"Ea-b = 0.06 - 0.12 eV
"Ea-I = 0.25 - 0.35 eV
"Ea-t = 0.35 - 0.45 eV
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Thermal kink pairs nucleating at adjacent MDI mediate the migration 0.
Migration barriers
1/3rd
! (reaction coordinate)
that of migration barriers in bulk

29. Isolated point defects in CuNb migrate from
one MDI to another

30. Isolated point defects in CuNb migrate from
one MDI to another

31. 0.45
0.4
Vacancy
I
KJ1t
t
Se
KJ3
!1
b1
•
t
KJ3´
a2
0.15
0.1
a1 L
!1
0.05
b1
b
t1
L
t1
L
0.2
t
t
I
I
0 a
•
KJ4
〈110〉
Cu
KJ4
0.25
Set 2
〈110〉
Cu
Se
t1
Step 1
t
Se
" E (eV)
a2 a1
KJ1
KJ2´
0.35
0.3
b
KJ2
〈112〉
Cu
a
〈112〉
Cu
Isolated point defects in CuNb migrate from
one MDI to another
Set 2
3L
Set 2
!1
b1
b
Interstitial
Vacancy
"Ea-b = 0.06 - 0.12 eV
"Ea-I = 0.25 - 0.35 eV
"Ea-t = 0.35 - 0.45 eV
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Thermal kink pairs nucleating at adjacent MDI mediate the migration 0.
Migration barriers
1/3rd
! (reaction coordinate)
that of migration barriers in bulk

32. Thermal kink pairs aid the migration process
b
0.4
Vacancy
I
KJ1
KJ2´
KJ4
I
3L
0.15
t1
a2
Se
L
t1
0.2
t
t
KJ3´
0.25
a1 L
!1
b1
t
〈110〉
Cu
I
2
Set 0.1
•
t
t
b
Se
" E (eV)
Se
t1
Step 2
•
c
0.35
0.3
!1
t
〈112〉
Cu
0.45
0.05
b1
0 a
Set 2
Set 2
!1
b1
b
Interstitial
Vacancy
"Ea-b = 0.06 - 0.12 eV
"Ea-I = 0.25 - 0.35 eV
"Ea-t = 0.35 - 0.45 eV
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Thermal kink pairs nucleating at adjacent MDI mediate the migration 0.
Migration barriers
1/3rd
! (reaction coordinate)
that of migration barriers in bulk

33. Thermal kink pairs aid the migration process
(a)
(b)
(c)
(d)
(e)
(f)
Vacancy
Interstitial
ΔEact = 0.35 - 0.45 eV
ΔEact = 0.60 - 0.67 eV
1nm
The width of the nucleating thermal kink pairs determines the barrier

34. 0.45
t
Multiple migration paths and detours
0.4
t
t
t
0.35
t
" E (eV)
0.3
I
I
0.25
t
0.2
b
Migration paths
(CI-NEB)
Interstitial
0.15
Vacancy
0.1
0.05
0 a
0
b
"Ea-b = 0.06 - 0.12 eV
"Ea-I = 0.25 - 0.35 eV
"Ea-t = 0.35 - 0.45 eV
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.
! (reaction coordinate)
•
Not all intermediate states need to be visited in every migration
•
The underlying physical phenomenon, however, remains unchanged

35. Entire migration path can be predicted
0.5
0.5
0.45
0.45
0.4
0.4
0.35
0.35
0.3
0.3
0.25
0.25
I
0.2
0.15
0.2
I
0.15
0.1
0.1
0.05
0.05
0
a
0
Dislocation model
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
KJ1
1
KJ1
0 KJ2
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
s
Key inputs to the dislocation model
b
Atomistics
0
〈112〉
Cu
Δ E (eV)
0.55
KJ2´
〈110〉
Cu
KJ3
KJ4
•
Interface misfit dislocation distribution
•
KJ4
1
s
KJ3´
K. Kolluri and M. J. Demkowicz,
Phys Rev B, 82, 193404 (2010)
Structure of the accommodated point defects
Analysis of the interface structure may help predict quantitatively
point-defect behavior at other semicoherent interfaces

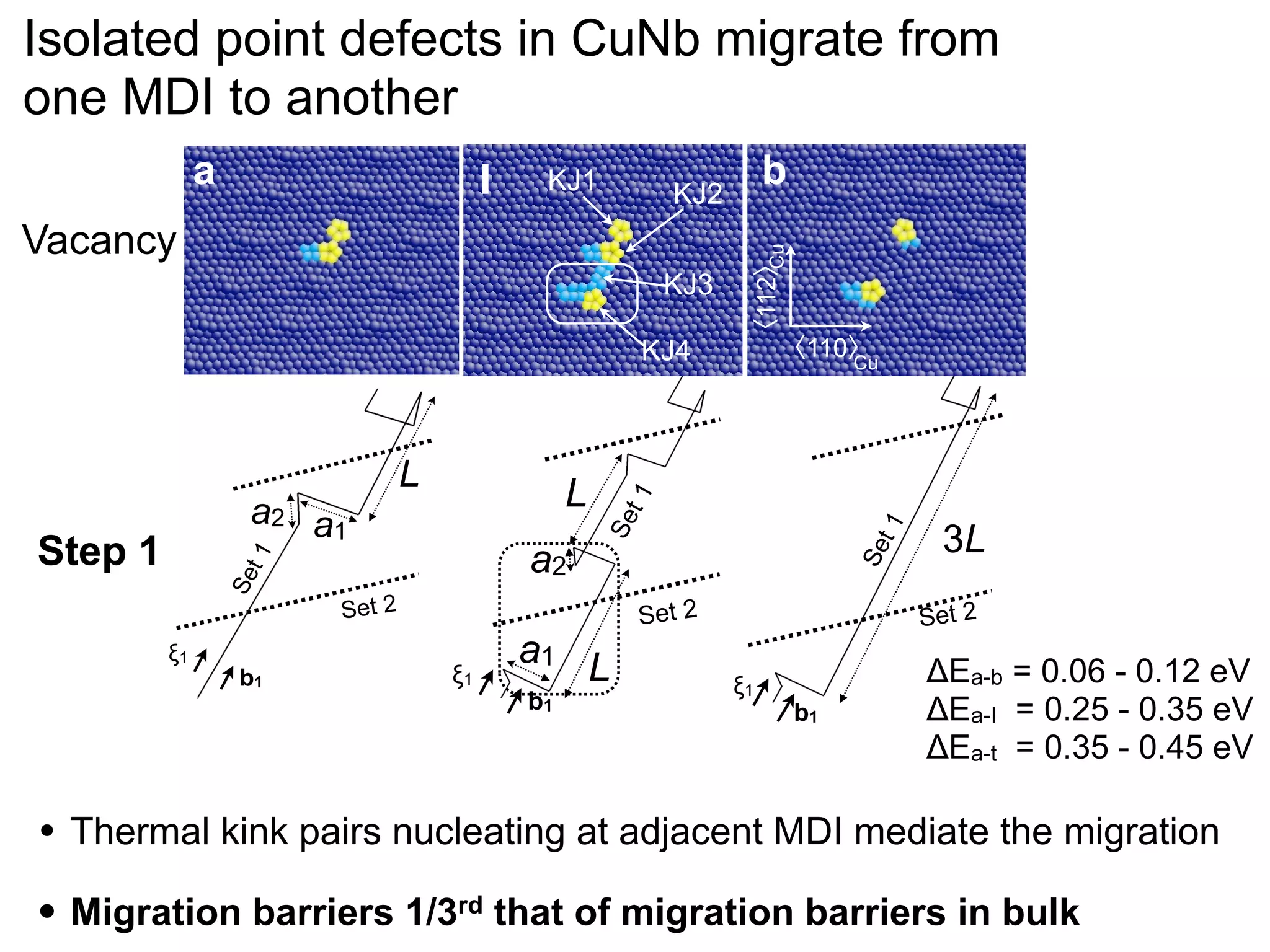
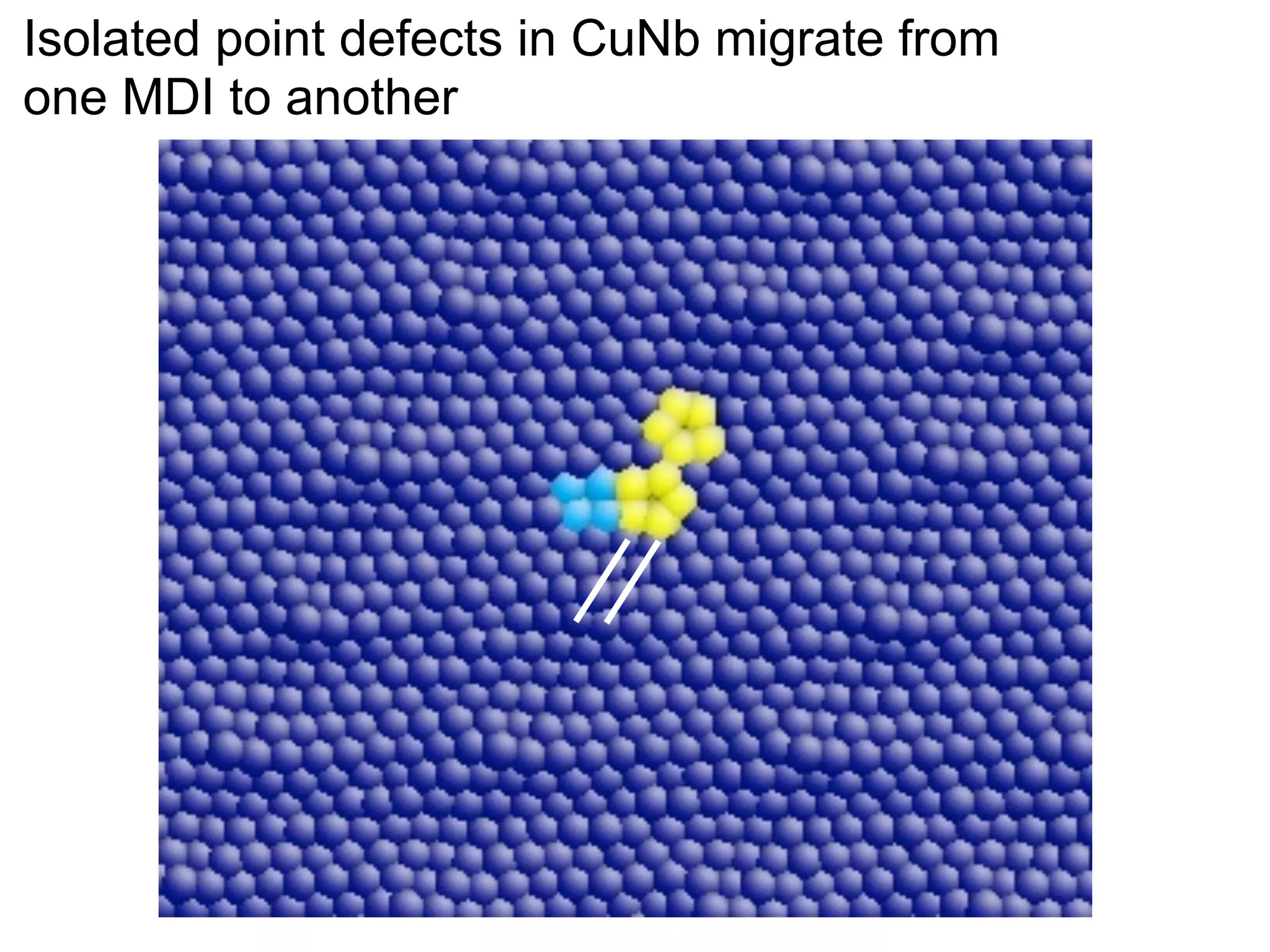
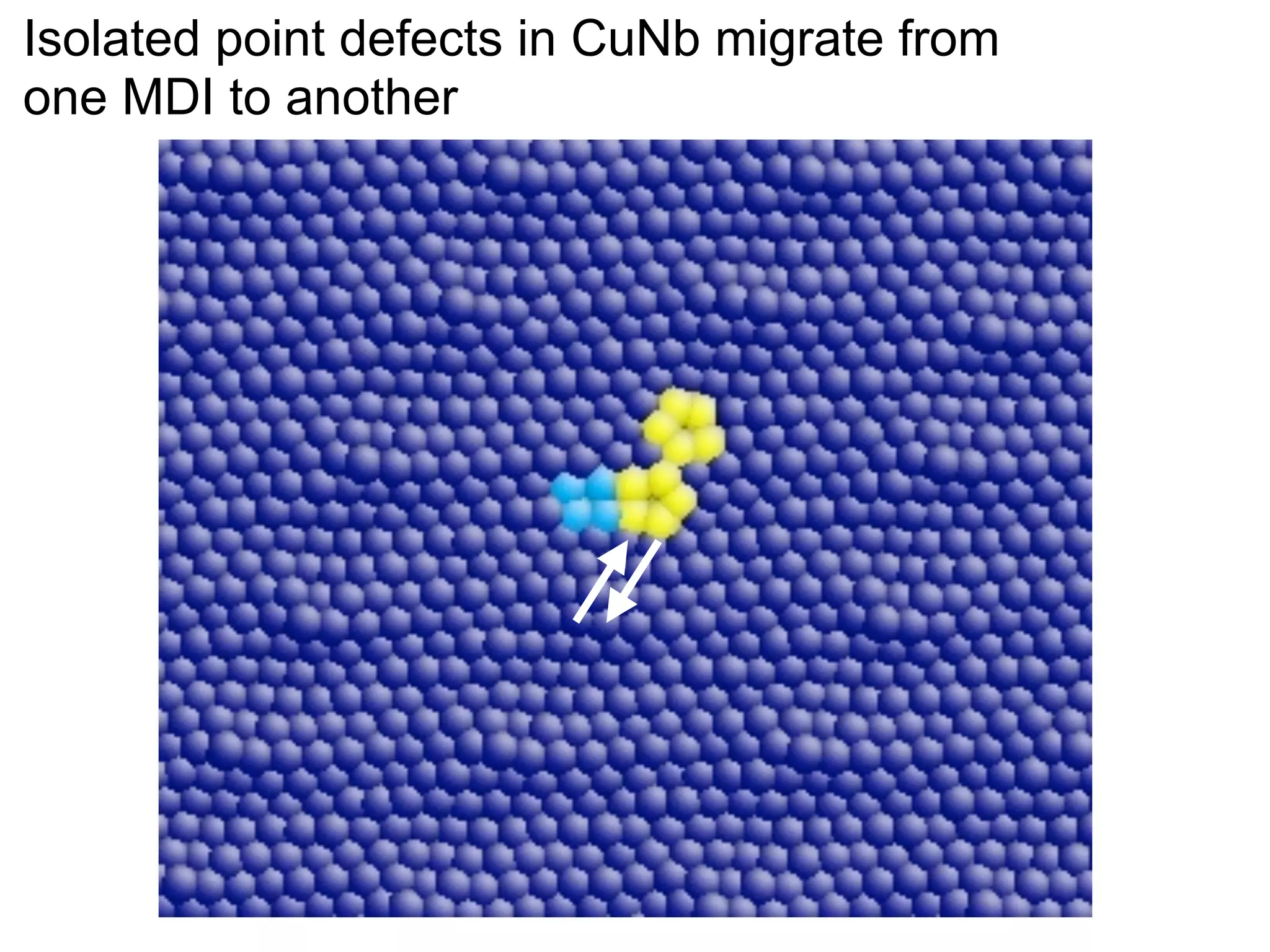
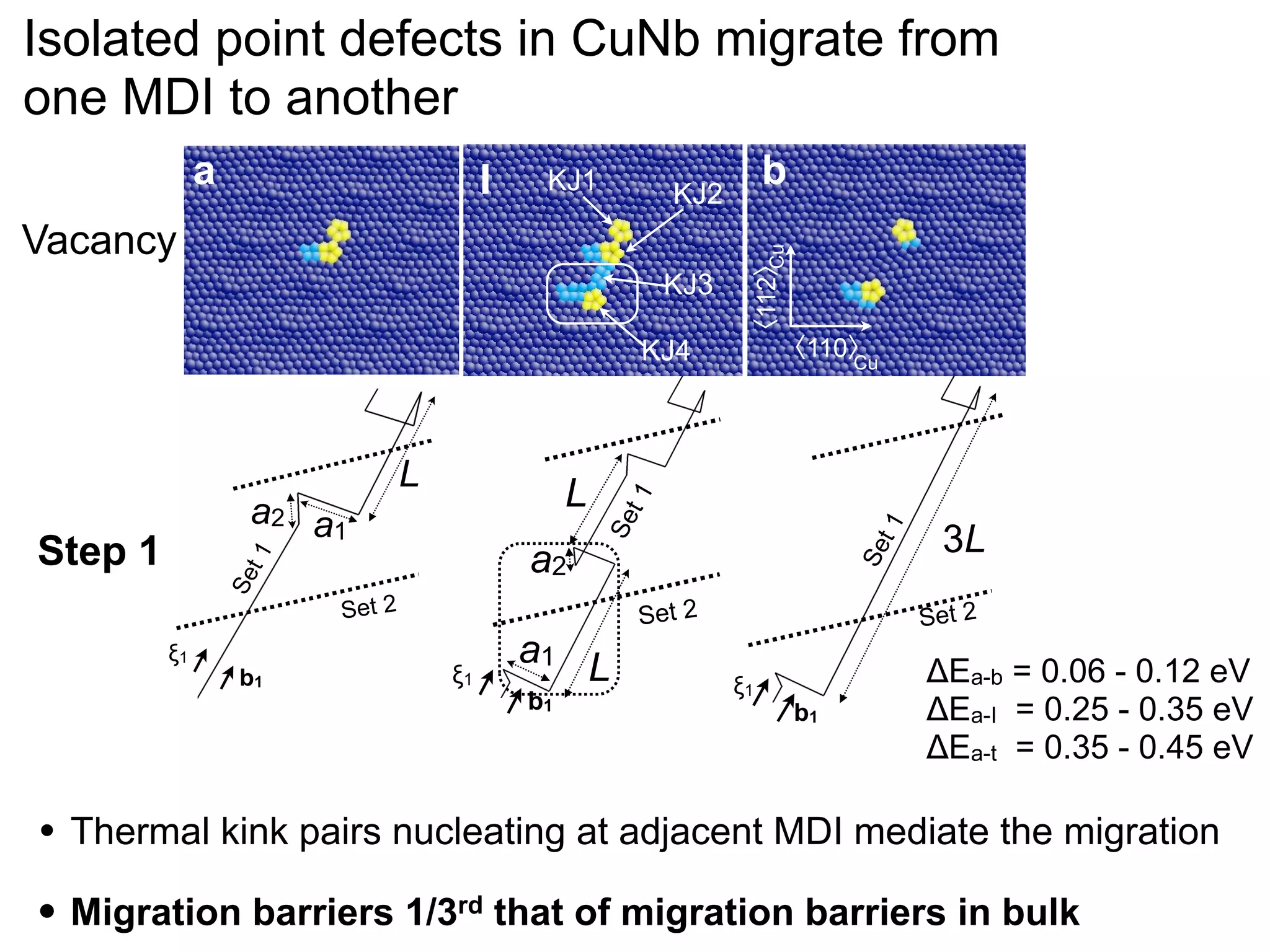
36. jog, which is assumed constant for all states in our dislocation
model [and therefore does not appear in Eq. (1)], actually varies
along the direct migration path. To estimate the core energy
of the kink-jog, we summed differences in atomic energies
between the core atoms and corresponding atoms in a defectfree interface. The kink-jog core is taken to consist of 19 atoms:
the 5-atom ring in the Cu terminal plane and the 7 neighboring
Cu and Nb atoms from each of the two planes adjacent to the Cu
terminal plane. Core volumes were computed in an analogous
way. The core energies of the migrating jog are plotted as
filled triangles in Fig. 15(a) and are in good semiquantitative
agreement with the overall energy changes occurring along
the direct migration path. Core volumes are plotted as filled
circles.
Figure 15(b) shows the Cu and Nb interface planes with
a point defect in the extended state B. Arrows mark the
locations of the two kink-jogs and red lines mark the nominal
locations of set 2 misfit dislocation cores. The numbers are
TABLE I. Transitions occurring during migration of individual
point defects that were considered in kMC simulations, their
corresponding activation energy barriers, and number of distinct end
states for a given start state.
Point defect migration rates from simulations
Transition
type
A→I
A→B
I (near A) → B
I (near A) → A
B→A
B→I
B→I
B→C
I (near C) → C
I (near C) → B
I →B
Activation energy
(eV)
Number of
distinct end states
0.40
0.40
0.15
0.15
0.35
0.35
0.20
0.35
0.15
0.15
0.15
2
2
1
1
1
2
1
1
1
1
1
205416-9
•
Hypothesis:
•
•
•
transition state theory is valid and
Rate-limiting step will determine the migration rate ≥ 0.4 eV
Validation:
•
kinetic Monte Carlo (since the migration path is not trivial)
•
Statistics from molecular dynamics

37. Migration is temperature dependent
Jump rate (ns-1)
0.1
1
=
0.01
0e
0.4eV
kB T
0.001
0.0001
1e-05
1300
1000
800
700
600
500
Inverse of Temperature (K-1)
K. Kolluri and M. J. Demkowicz,
Phys Rev B, 85, 205416 (2012)
•
Migration rates are reduced because there are multiple paths
•
Transition state theory may be revised to explain reduced migration rates

38. Migration is temperature dependent
Jump rate (ns-1)
0.1
1
=
0.01
0e
0.4eV
kB T
0.001
0.0001
1e-05
1300
1000
800
700
600
500
Inverse of Temperature (K-1)
K. Kolluri and M. J. Demkowicz,
Phys Rev B, 85, 205416 (2012)
•
Migration rates are reduced because there are multiple paths
•
Transition state theory may be revised to explain reduced migration rates

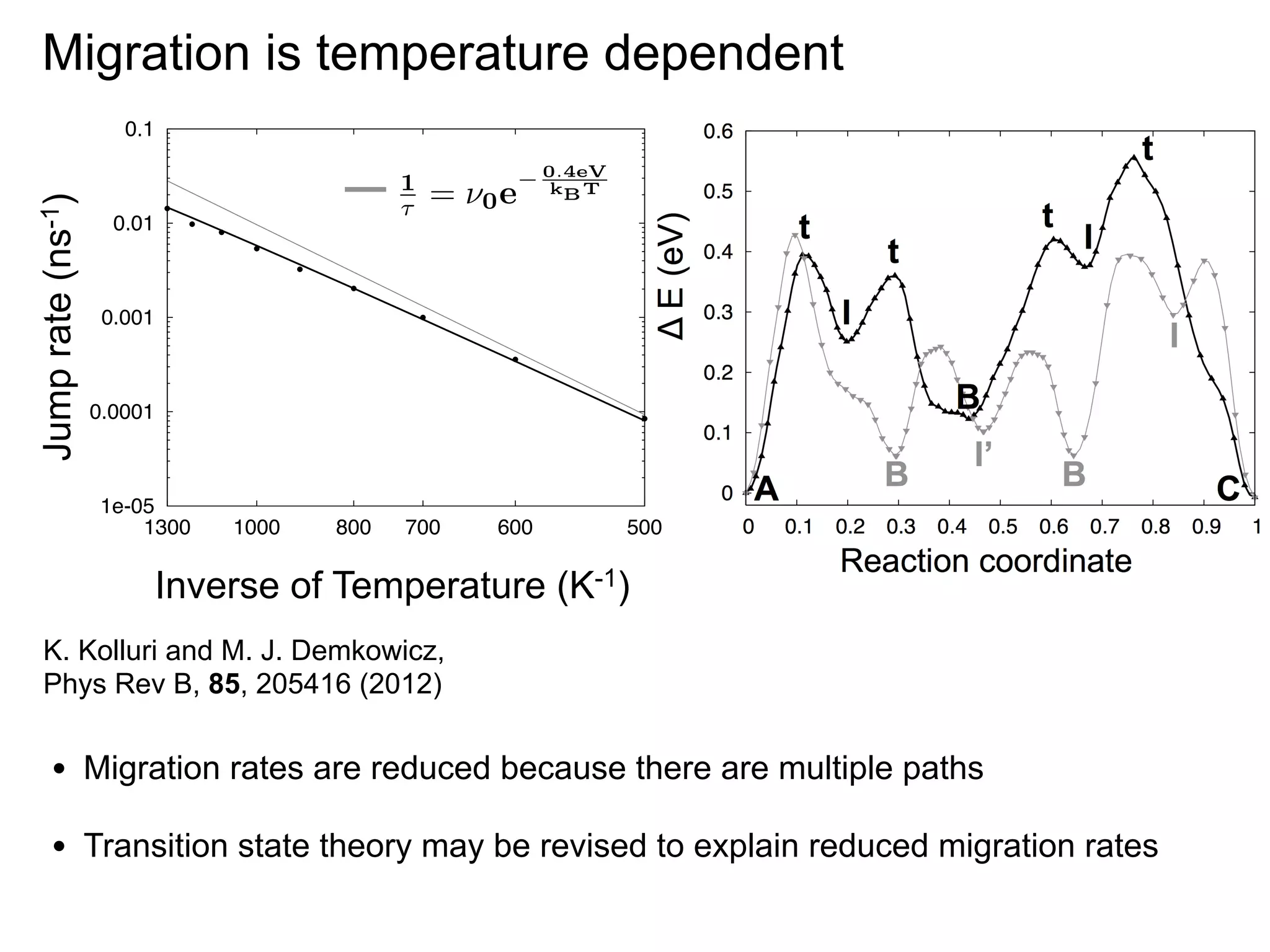
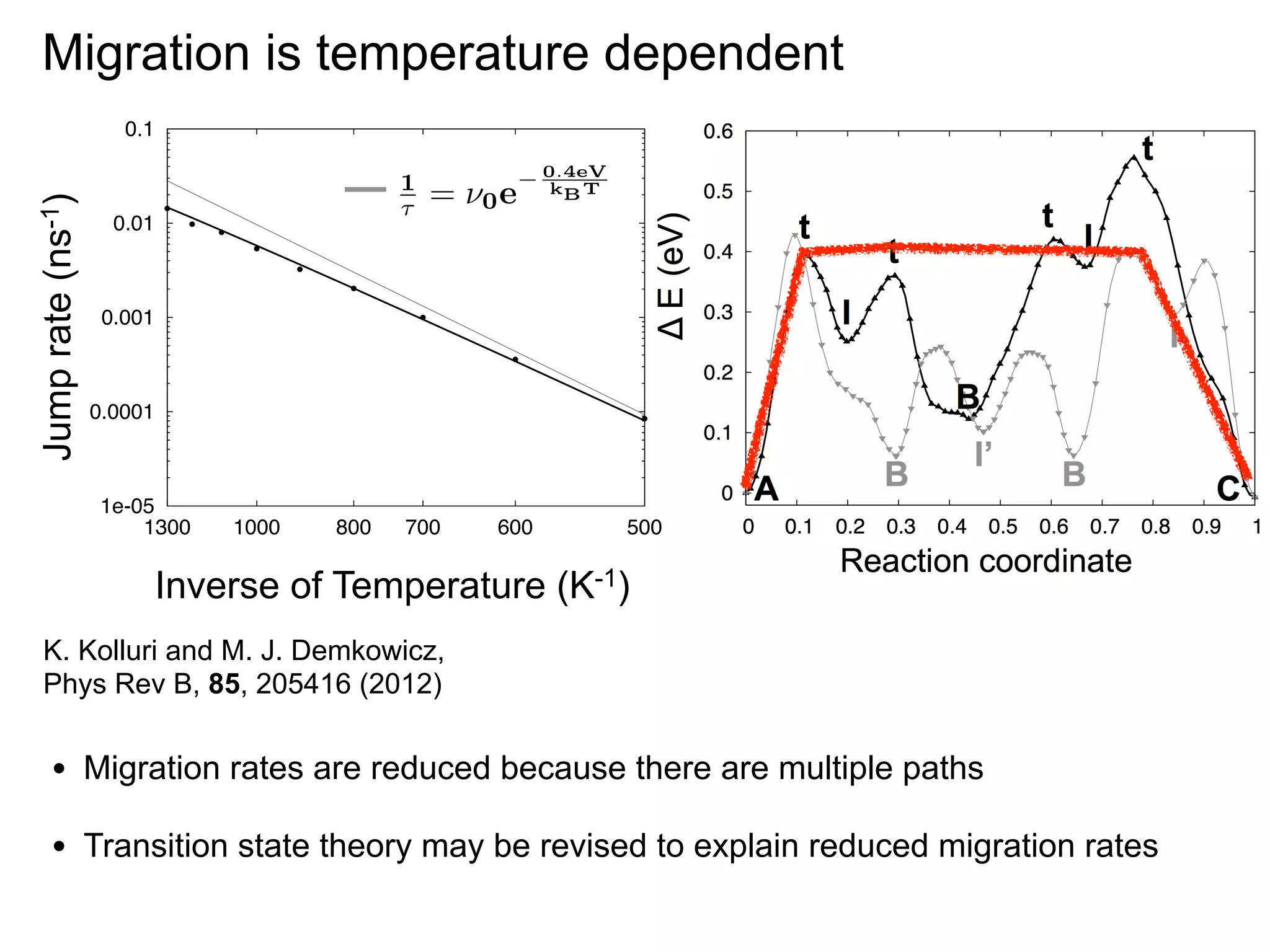
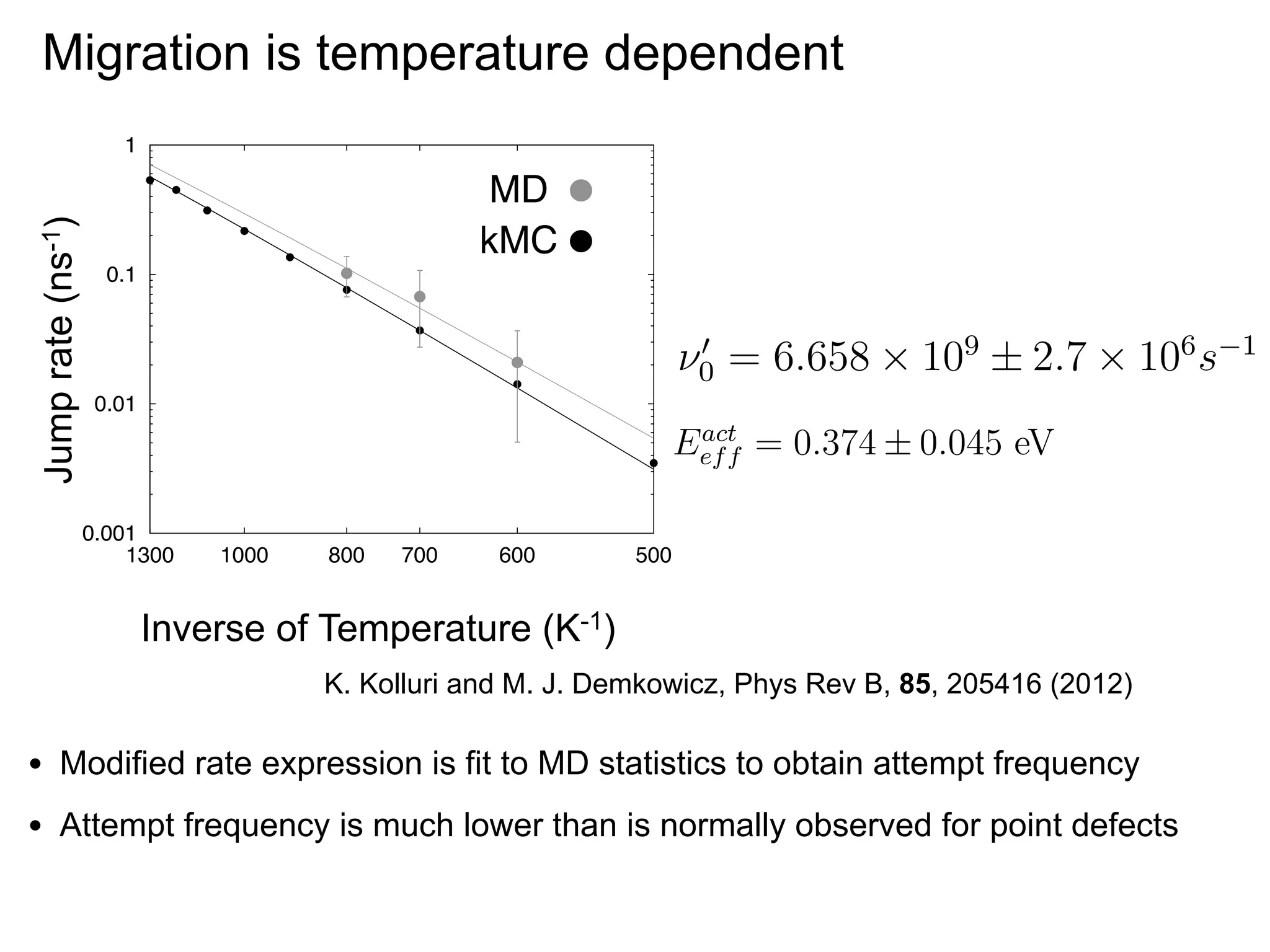
39. ln[(s!)p(t/τ,s)] = s ln(t/τ ) − t/τ.
(10)
Migration is temperature dependent
s are obtained for all three temperatures, confirming
0.1
tion that point defect1migration follows a Poisson
⇥
= 0 k 1T e
ig. 17). The jump rates for each temperature,
0.01
1
= 0e
y fitting, are plotted in Fig. 16(b) as filled gray
h uncertainties corresponding to the error in the
0.001
es fit. The gray line is the least-squares fit of Eq. (8)
obtained from MD. The activation energy obtained
0.0001
act
MC model (Eeff = 0.398 ± 0.002 eV) is well within
nty of 1e-05 activation energy found by fitting the MD
the
500
act
y, Eeff =1300 1000 0.045700 600
0.374 ± 800 eV.
Inverse of Temperature (K )
ctive attempt frequency for defect-1migration obfittingKolluri and M. J. Demkowicz, = 6.658 × 109 ± 2.7 ×
K. the MD data is ν0
Phys Rev several orders of
is value is B, 85, 205416 (2012) magnitude lower than
mpt frequencies for point defect migration in fcc
• Migration −1 .72–74 A mechanistic interpretation paths
12
14 rates are reduced because there are multiple
, 10 −10 s
ow migration attempt frequency is not immediately
• Transition state theory may be revised to explain reduced migration rates
g. One possible explanation is that it arises from
number of atoms participating in the migration
Jump rate (ns-1)
Eact
e
kB T
B
0.4eV
kB T

40. act
model(Eef f = 0.398 ± 0.002 eV) is w
Migration is temperature dependent
a
by fitting the MD data, namely Ee
Jump rate (ns-1)
1
MD
kMC
0.1
act
model(Eef f = 0.398 ± 0.002 eV) is well wi
act
by fitting the MD data, namely Eef f = 0
0
⌫0 = 6.658 ⇥ 109 ± 2.7 ⇥ 106 s
0.01
1
0
act
tained by0.374 ± 0.045 MD 0data is ⌫0
fitting the eV ⌫ 0 = 6.658 ⇥
Eef f =
0.001
1300
for defect migration obtained typical t
of magnitude lower than by fittingat
1000
800
700
600
500
69–71
value is 1012 1014
namelyseveral orderssof1 magnitude mec
. A lowe
Inverse of Temperature (K-1) migration in fcc Cu, namely 1012 1014
frequency is not immediately forth
K. Kolluri and M. J. Demkowicz, Phys Rev B, 85, 205416 (2012)
low migration attempt frequency is not im
•
•
the large number of atoms particip
Modified rate expression is fit to MD statistics to obtain attempt frequency
is that it arises from the large number of
Attempt frequency is much lower than for migration of for migration of compa
is normally observedcompact point defe
attempt frequency for point defects
frequency because it involves the m
der of the Einstein frequency because it i

41. Takeaways from fcc-bcc semicoherent interfaces
•
Interface has defect trapping sites
– density of these sites depends on interface structure
•
Point defects migrate from trap to trap
– migration is multi-step and involves concerted motion of atoms
– migration can be analytically represented
How much of this knowledge can be ported to ceramics?
•
Electrostatics
•
covalency
•
multiple species

42. Takeaways from fcc-bcc semicoherent interfaces
•
Interface has defect trapping sites
– density of these sites depends on interface structure
•
Point defects migrate from trap to trap
– migration is multi-step and involves concerted motion of atoms
– migration can be analytically represented
How much of this knowledge can be ported to ceramics?
•
Electrostatics : MgO - highly ionic and simple to model
•
covalency
•
multiple species

43. Model systems, methods etc.
•
MgO grain boundaries using the simplest of ionic potentials available
1 nm
•
Fixed charge on each atom (this potential has full charge)
•
Molecular statics and dynamics (at 2000K)
<100>
<100> +ø/2
Eij = Ae
rij
⇢
C
6
rij
+
Cqi qj
1
✏rij

44. Model systems
•
Grain boundaries (3.5º to 10º)
1 nm
3.476º, 4.969º, 7.5º, 10.393º
d = 34Å

45. Model systems
•
Grain boundaries (3.5º to 10º)
1 nm
3.476º, 4.969º, 7.5º, 10.393º
d = 15Å

46. Ground-state structure of (some) grain boundaries
0.5
0
-0.5
-1
-1.5
-2
0
0.5
1
Electrostatics:
2 MgO units less at an MDI (O-lattice points)
1.5
2

47. Typical interface (one with misfit dislocations)
7.5º twist
boundary

48. Vacancy delocalizes on the misfit dislocation
Electrostatics
•
Farther, the “halves” of the vacancy, the lower is the energy
•
But, not farthest!

49. Vacancy delocalizes on the misfit dislocation
0.45
0.4
Ef (eV)
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
•
0
8
1
7
2
6
3
5
4
4
5
3
6
2
7
1
8
0
Differences with metal-metal interfaces
•
Vacancies delocalize at misfit dislocations
•
MDIs hollow and can not reconstruct

50. Summary of where O vacancy traps
0.15
0.1
Ef (eV)
0.05
At MDI
0
-0.05
Adjacent planes
-0.1
-0.15
-0.2
-0.25
-0.3
0
1
7
2
6
3
5
4
5
3
6
2
7
1
8
localized
at MD

51. Summary of where Mg vacancy traps
0.2
0.15
0.1
Ef (eV)
0.05
At MDI
0
Adjacent planes
-0.05
-0.1
-0.15
-0.2
-0.25
-0.3
-0.35
0
7
1
6
2
5
3
4
4
3
5
2
6
1
localized
7
at MD

52. Interaction energies
Wint = Welastic + Welectrostatic
nL
1
a
2 2
µb a
1
Welastic ⇡
8⇡(1 ⌫) nL
1
qq1 q2 1
1 q2
WWelectrostatic ⇡
=
electrostatic
4⇡✏0 nL
4⇡✏0 ✏ nL
1
a
p0
2
a0
a =
2
µ = 132-141 GPa
155 GPa
b =
0.32
⌫ = 0.18
L = b
q 1 , q2
0.63(0.68)
eV
Welastic =
n
0.606
eV
Welectrostatic =
n
•
✏0
a0
= 1e
= 8.85e 12 Ohm
= 4.212˚
A
1
m
✏this model = 7.92
n - number of nearest neighbors
Elastic energies are perhaps an overestimate!
1

53. Oxygen vacancy transport in GB with misfit dislocations
Oxygen vacancy at
7.5º GB

54. Direct observation
t0
t0 +4 ps
t0 +8 ps
0.2 - 0.3 eV
0.3 eV
NOT TO SCALE
•
Migration barriers 1/10th that of migration barriers in bulk

55. Summary
Metals:
•
Interface has defect trapping sites
– density of these sites depends on interface structure
•
Point defects migrate from trap to trap
– migration is multi-step and involves concerted motion of atoms
– migration can be analytically represented
Ceramics:
•
Defects trapped at and migrate from one misfit dislocation to another
•
Electrostatics in the model ceramics play greater role
•
Defects migrate faster and anisotropic

56. Point defect migration along the interface depends on
0
the distance between defects on misfit dislocations
1 nm
Cu-V KS
0
0.2
0
150
0.2
0.4
100
0.4
0.6
50
0.6
0.8
1
0
0.8
1

57. Oxygen vacancy at grain boundaries at 5º twist
3.3
Ef (eV)
3.25
3.2
3.15
3.1
3.05
3
2.95
2.9
0.48
0.49
0.5
0.51
0.52
0.53
0.54
0.55
0.56
z axis
•
Similarities with metal-metal interfaces
•
dislocations and MDIs are preferred sites for point defects

58. Oxygen vacancy at grain boundaries at 5º twist
3.3
Ef (eV)
3.25
3.2
3.15
3.1
3.05
3
2.95
2.9
0.48
0.49
0.5
0.51
0.52
0.53
0.54
0.55
0.56
z axis
•
Differences with metal-metal interfaces
•
point defects reside in adjacent planes at MDIs