Download to read offline
![Weirdness in Phases
ΔT (θ,φ )
T
=∑∑ al,m Ylm(θ,φ)
| | [ ]ml,ml,ml, ia=a φexp
For a homogeneous and isotropic Gaussian
random field (on the sphere) the phases are
independent and uniformly distributed. Non-
random phases therefore indicate weirdness..](https://image.slidesharecdn.com/colessabino-150901174309-lva1-app6891/75/Adventures-with-the-One-Point-Distribution-Function-28-2048.jpg)
![Extreme Value Statistics
(exact)
Given the distribution of X, what is the
distribution of Xmax?
[ ]
[ ] 1
21max
1max
)()()(
)(
)Pr(.....)Pr()Pr()Pr(
).....sup(:}{
−
=⇒
=
≤××≤×≤=≤
=
n
n
n
ni
zFznfzg
zF
zXzXzXzX
XXXX](https://image.slidesharecdn.com/colessabino-150901174309-lva1-app6891/75/Adventures-with-the-One-Point-Distribution-Function-38-2048.jpg)
Uploaded byPeter Coles
Adventures with the One-Point Distribution Function
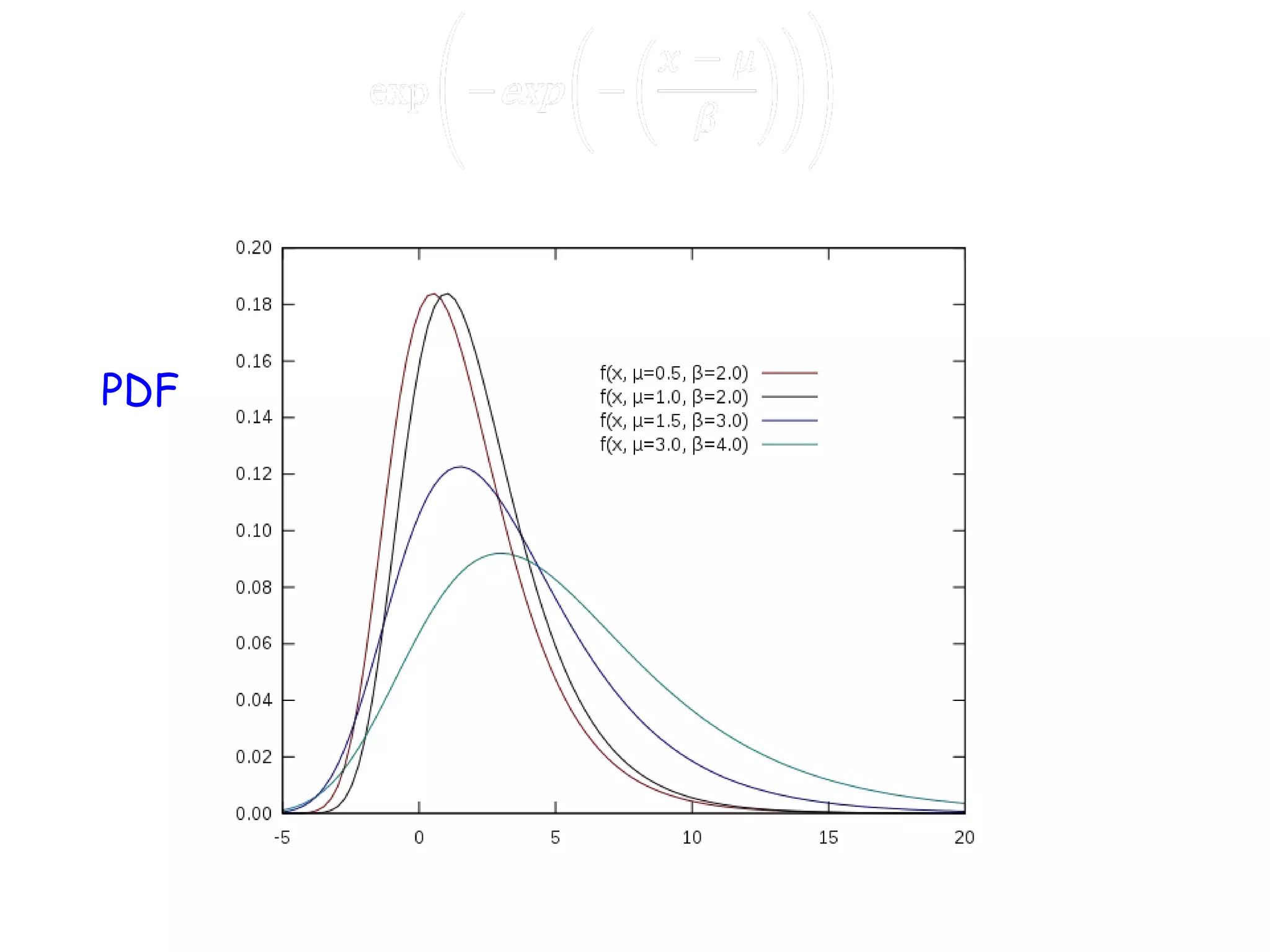
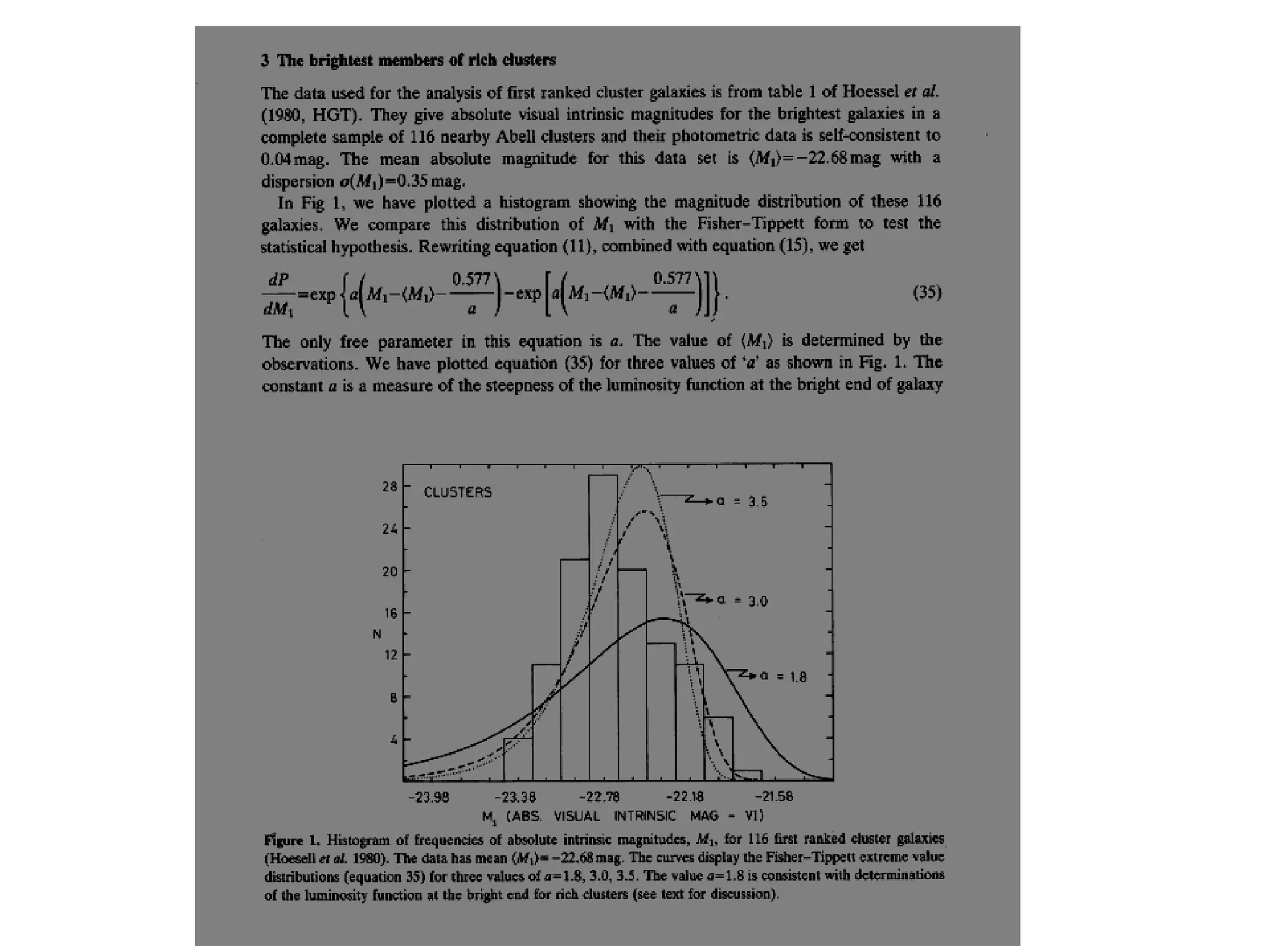
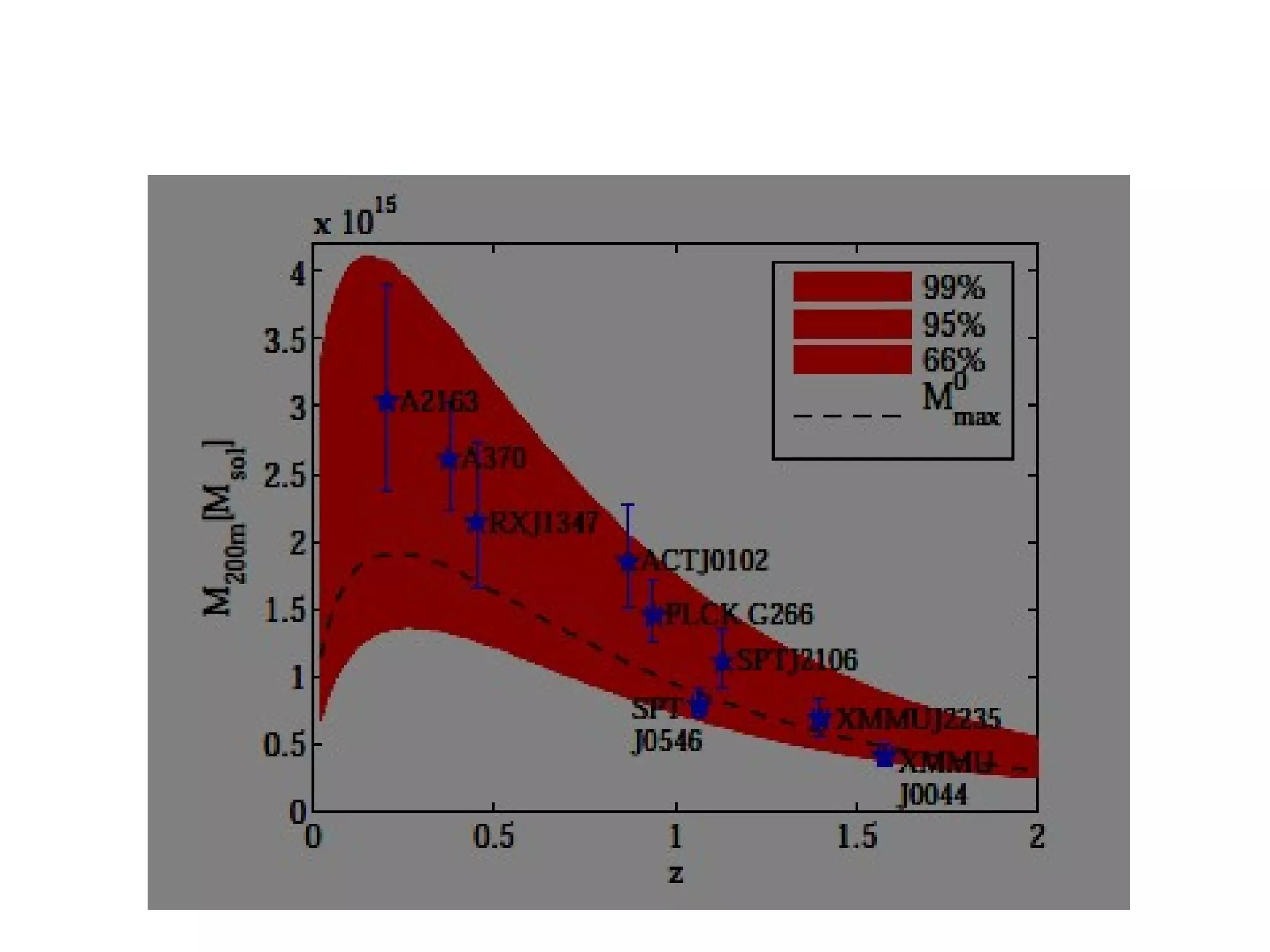
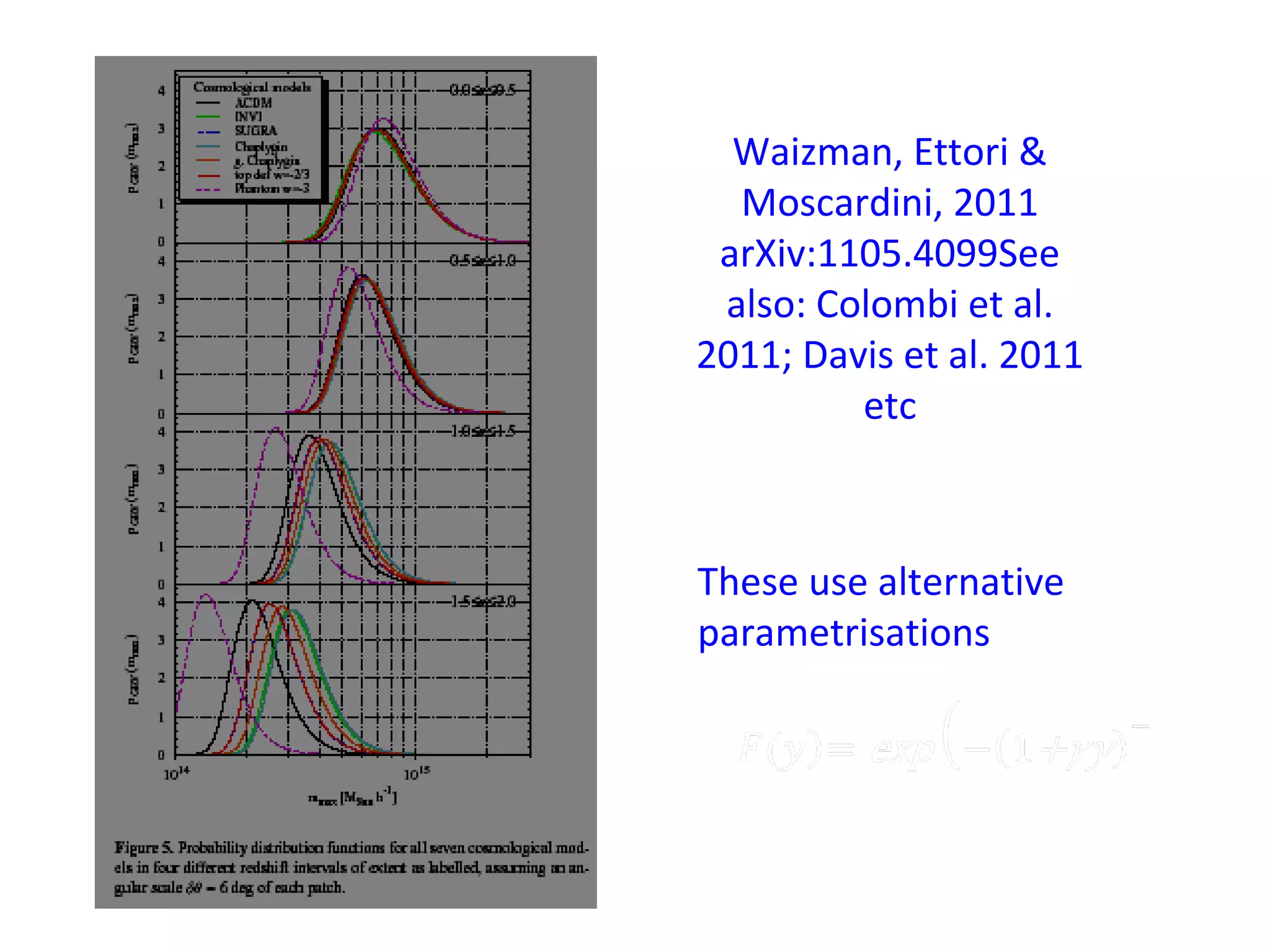
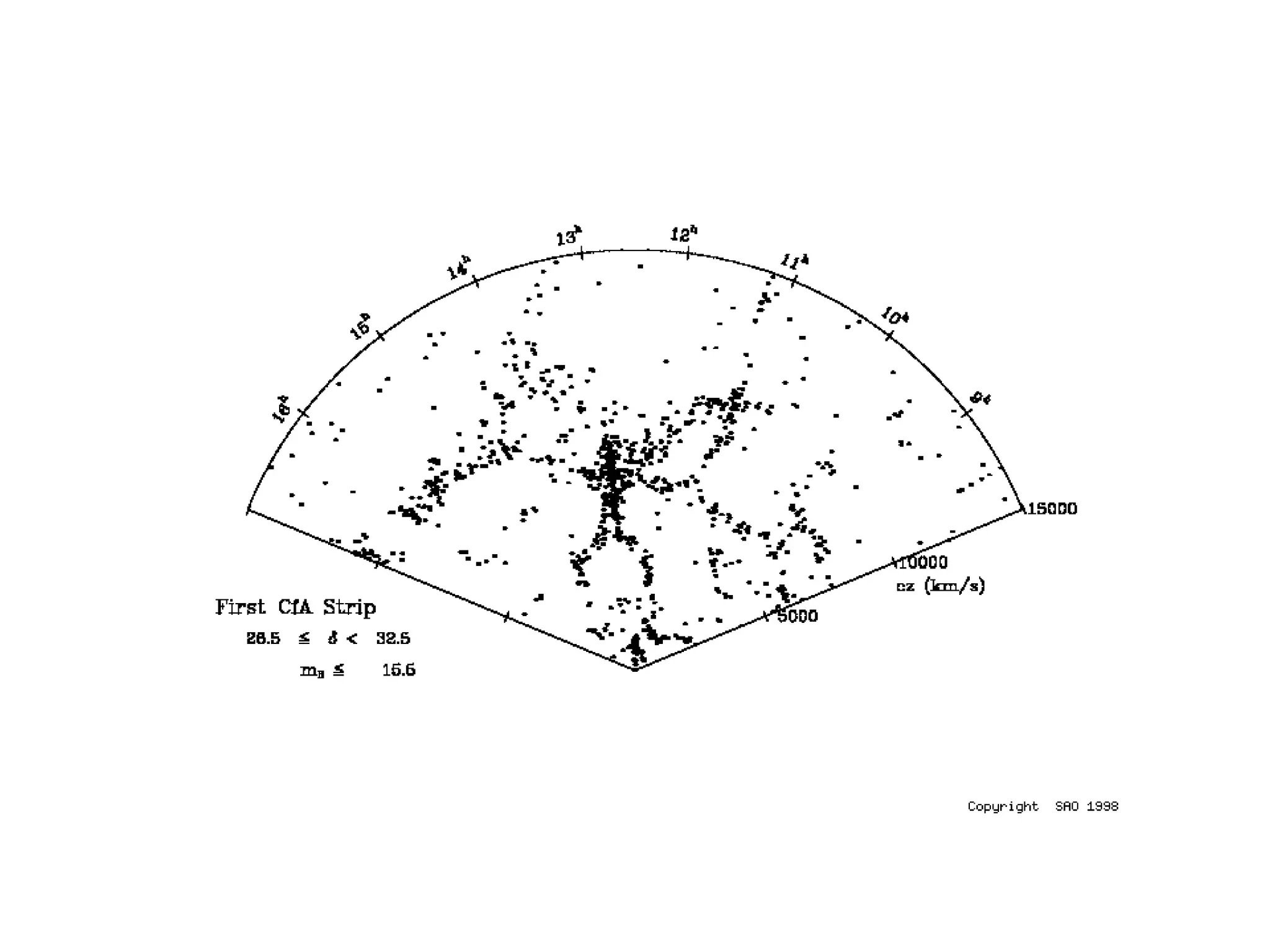
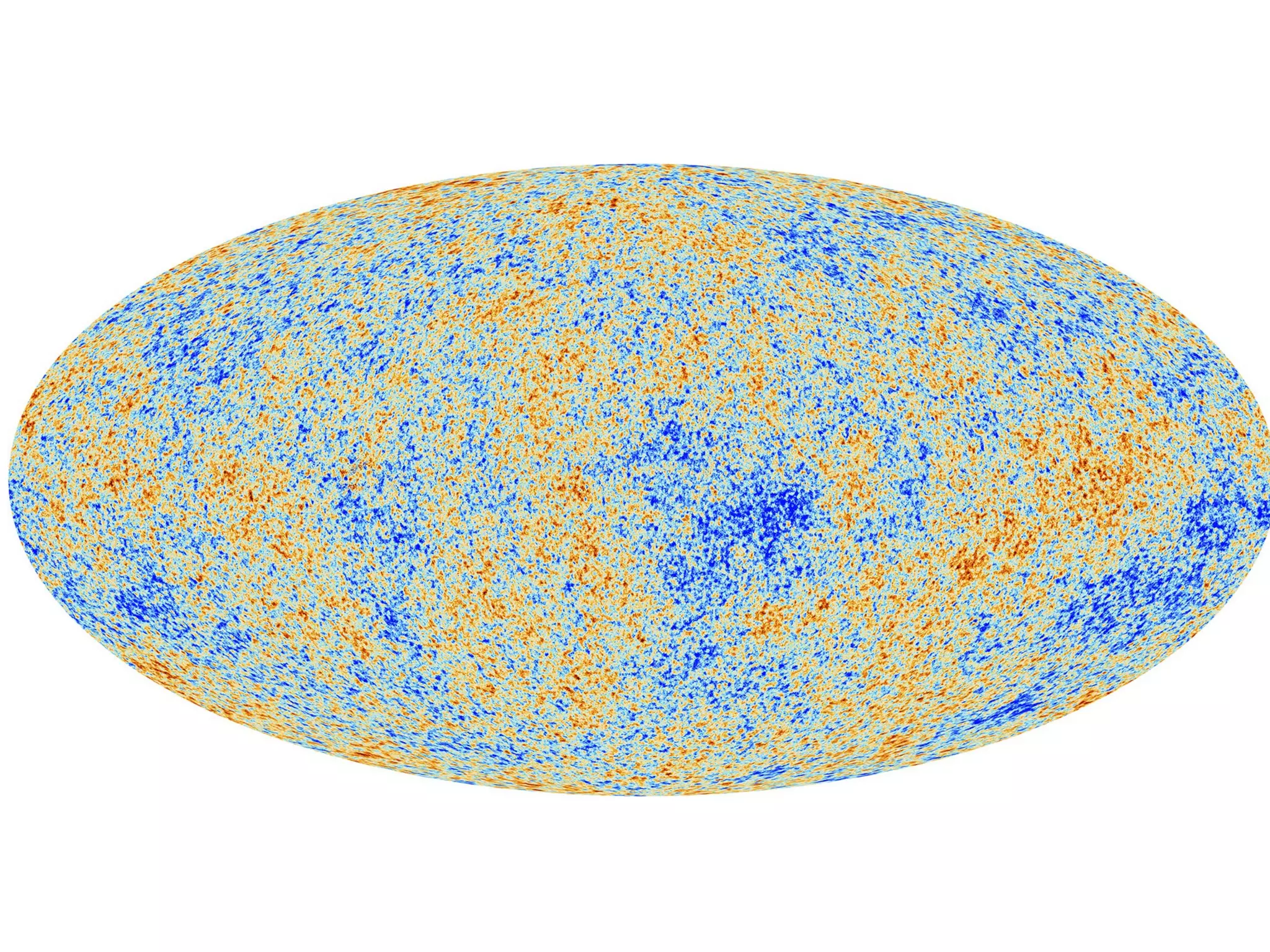
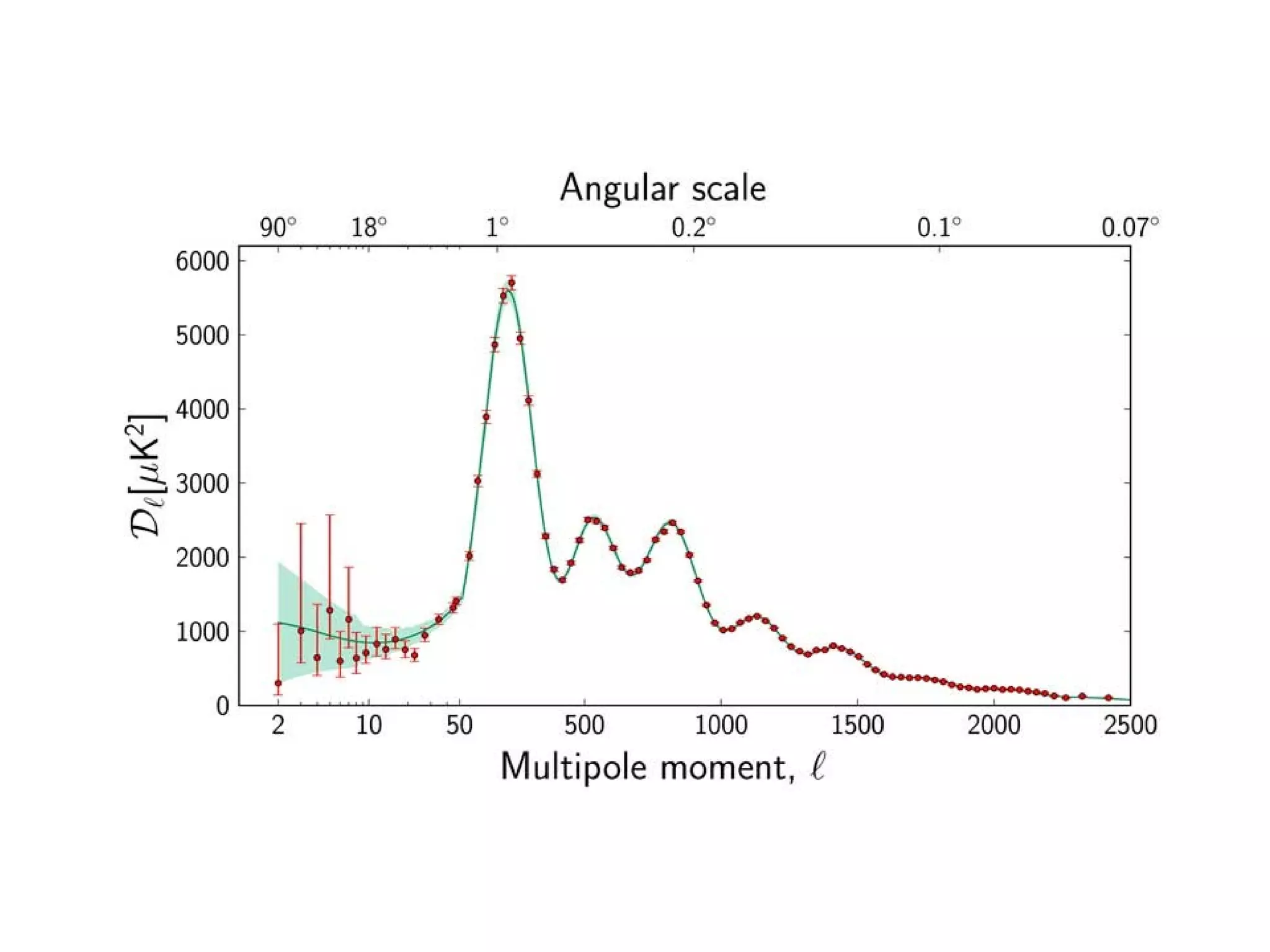
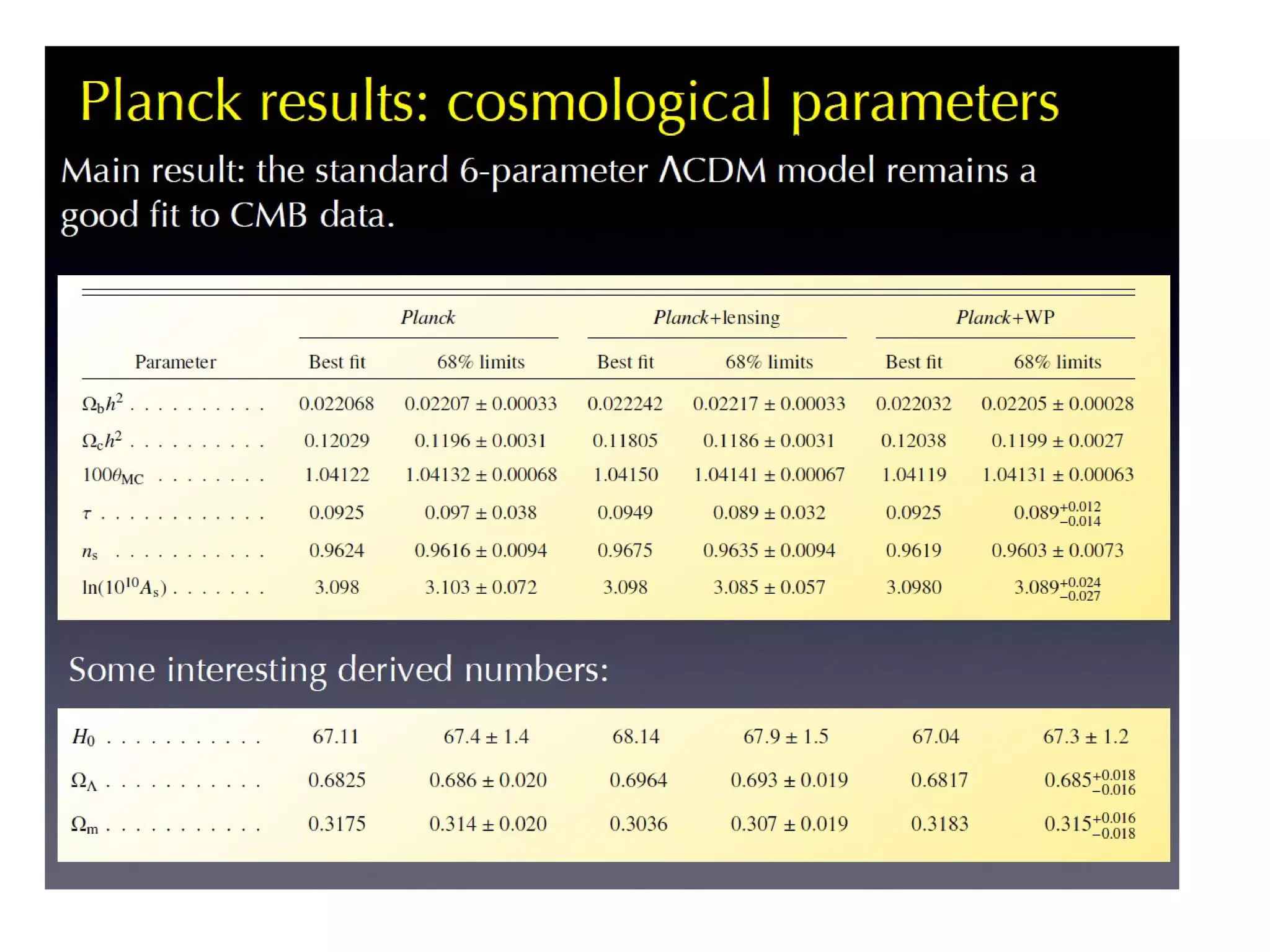
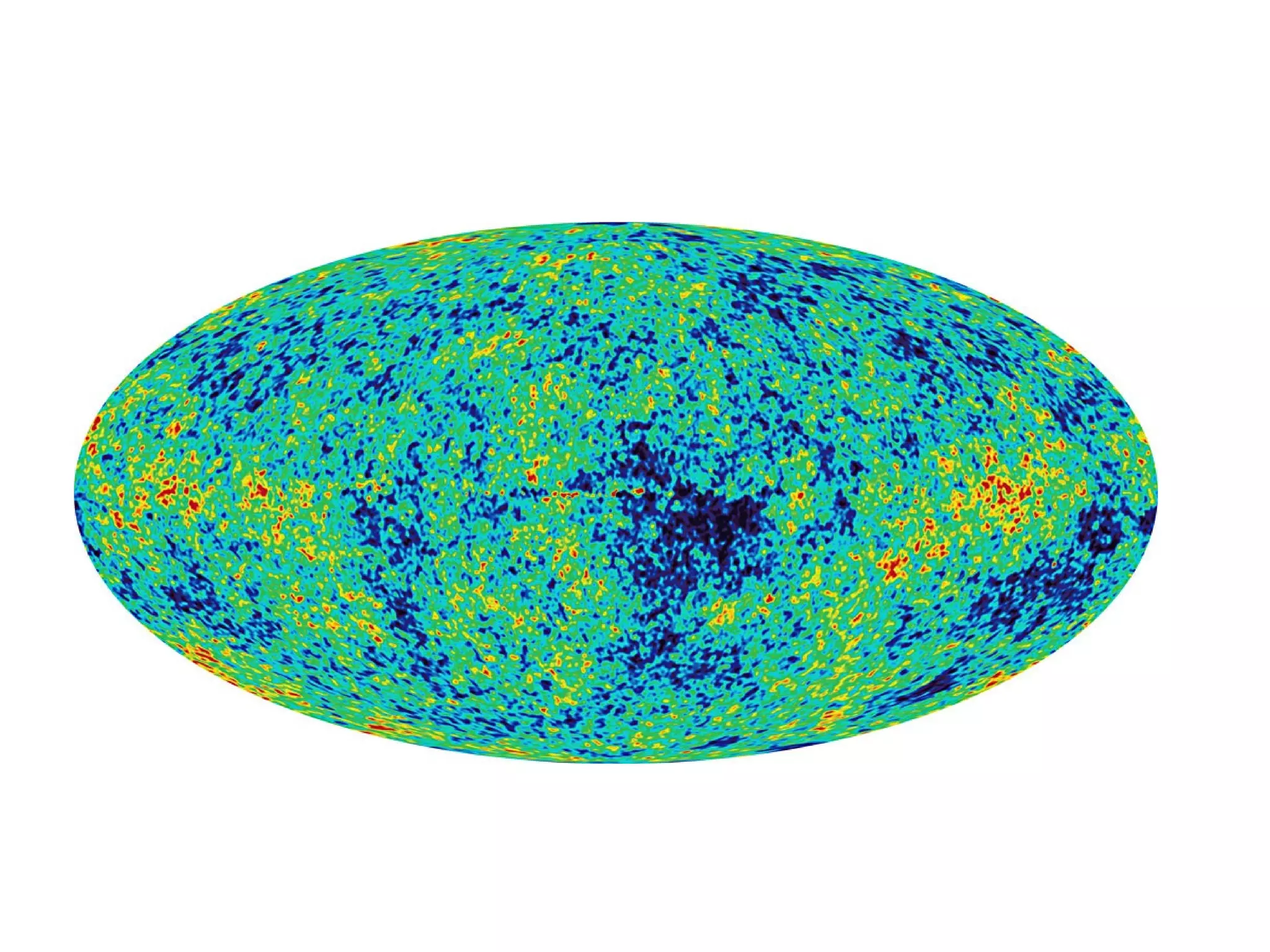
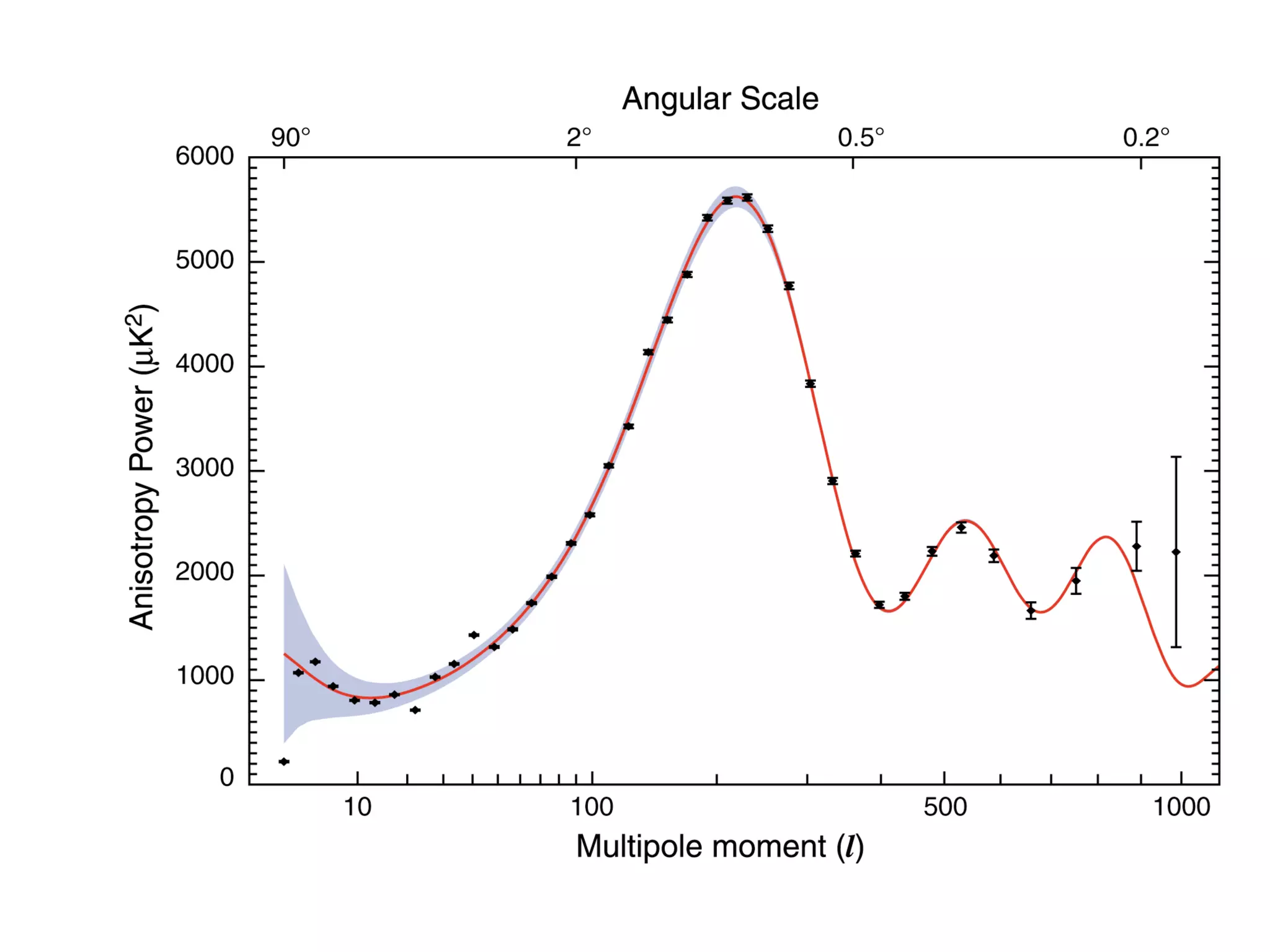
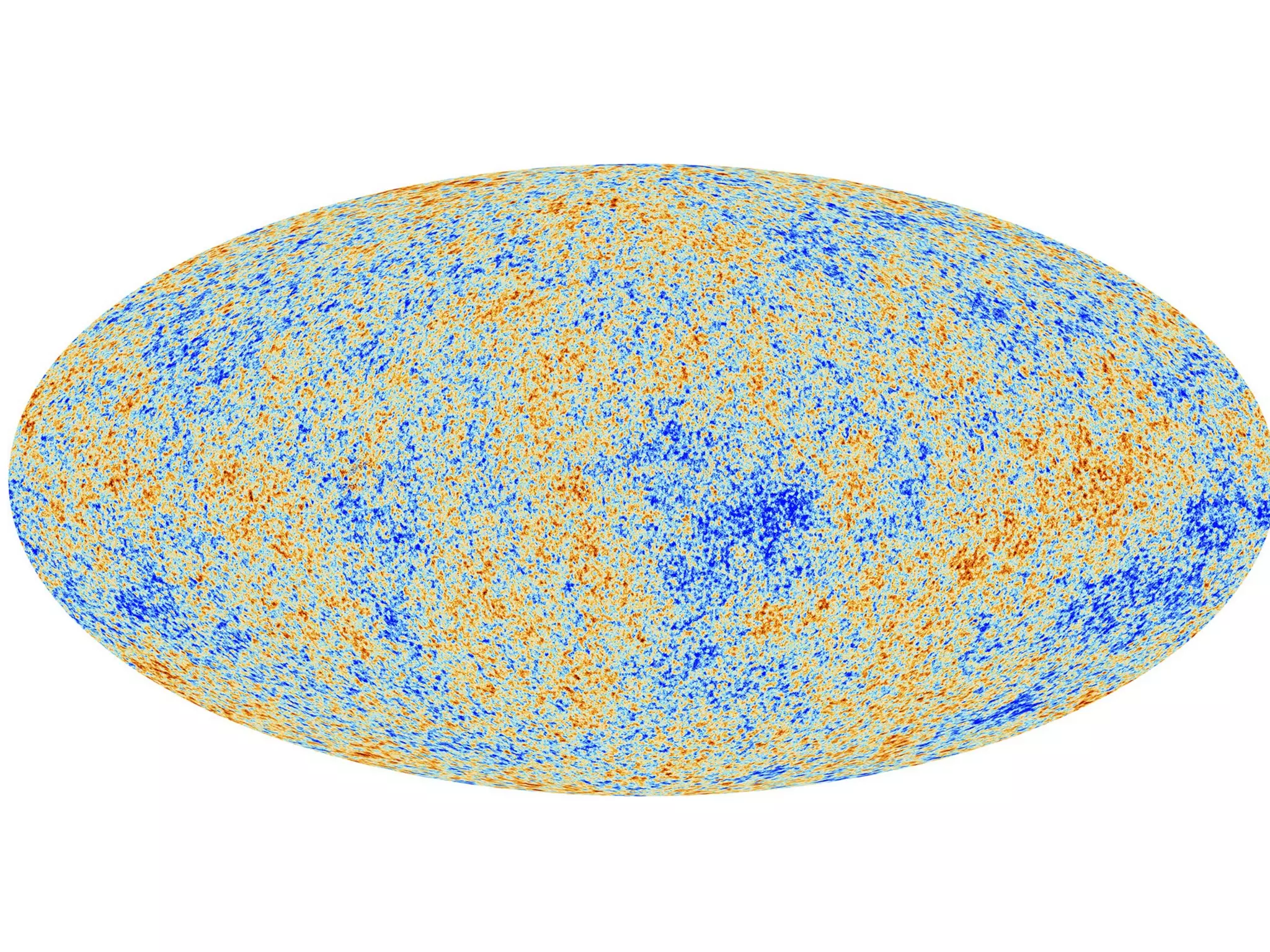
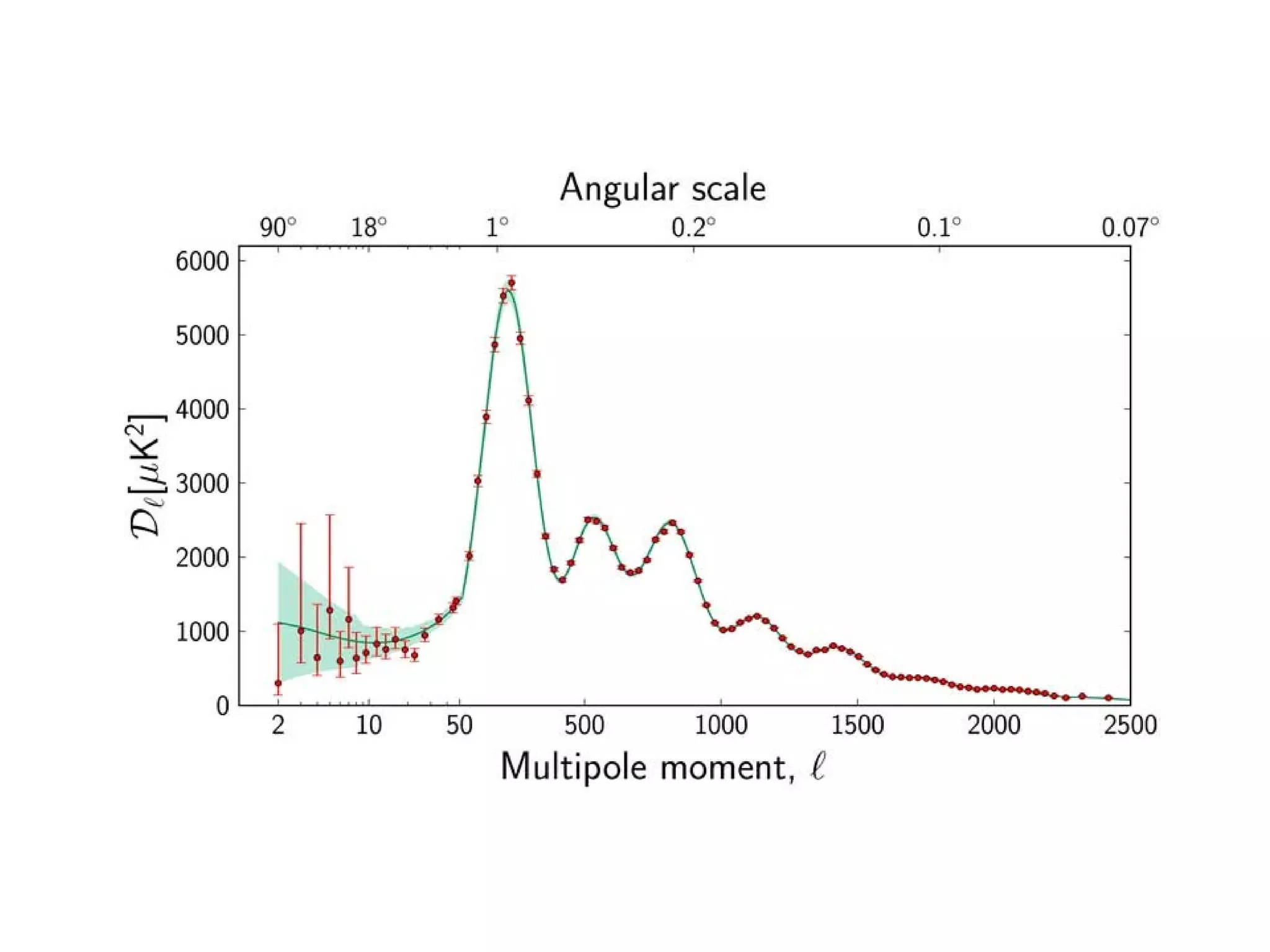
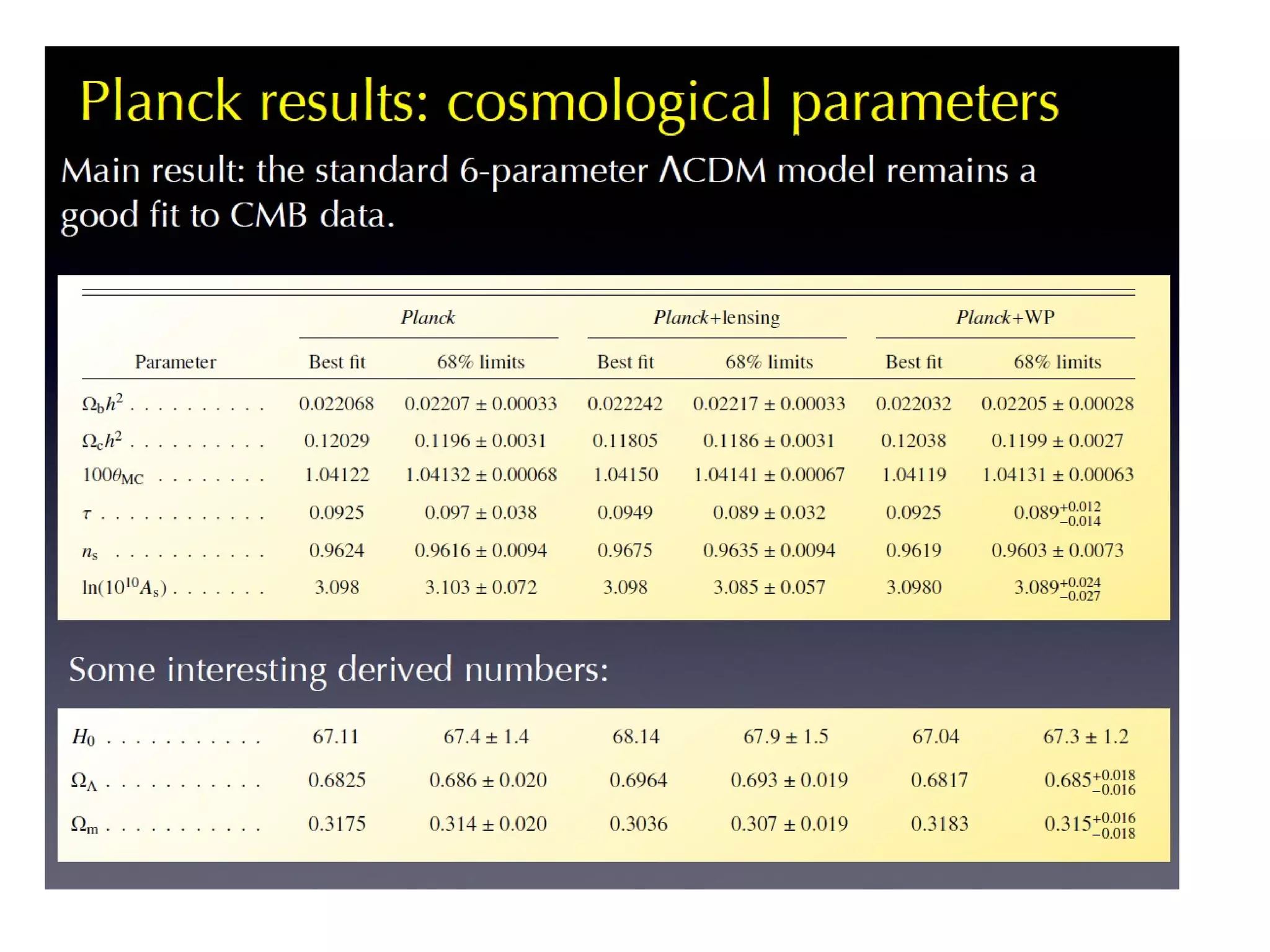
The document discusses the complexities and challenges of modern cosmology, highlighting the importance of statistics and data analysis. It critiques aspects of the standard cosmological model, emphasizing the need to reconsider discarded data to uncover potential unknowns. The conclusion suggests that while the constraints of standard cosmology are tight, the abundance of data offers new opportunities for discovery.
More Related Content
Similar to Adventures with the One-Point Distribution Function
More from Peter Coles
Adventures with the One-Point Distribution Function
- 1. Adventures with the One-PointDistribution Peter Coles Castiglioncello, Italy 1st September 2015
- 2.
- 3. “The Essence of Cosmologyis Statistics” George McVittie
- 12.
- 13.
- 14. Precision Cosmology “…as weknow, there are known knowns; there are things we know we know. We also know there are known unknowns; that is to say we know there are some things we do not know. But there are also unknown unknowns -- the ones we don't know we don't know.”
- 15. Questionable Aspects ofthe Standard Cosmology •General Relativity •Cold Dark Matter •Cosmological Constant •Cosmological Principle •Primordial Gaussian fluctuations •Inflation •Baryons •Neutrinos •Radiation…
- 16. Ingredients of theStandard Cosmology •General Relativity •Cold Dark Matter •Cosmological Constant •Cosmological Principle •Primordial Gaussian fluctuations •Inflation •Baryons •Neutrinos •Radiation…
- 21.
- 22. Direct versus Inverse Reasoning Theory (Ω,H0…) Observations
- 23. Cosmology is anexercise in data compression Cosmology is a massive exercise in data compression... ….but it is worth looking at the information that has been thrown away to check that it makes sense!
- 24. “If tortured sufficiently,data will confess to almost anything” Fred Menger
- 25. A)!|P(MM)|P(A ≠ Beware theProsecutor’s Fallacy!
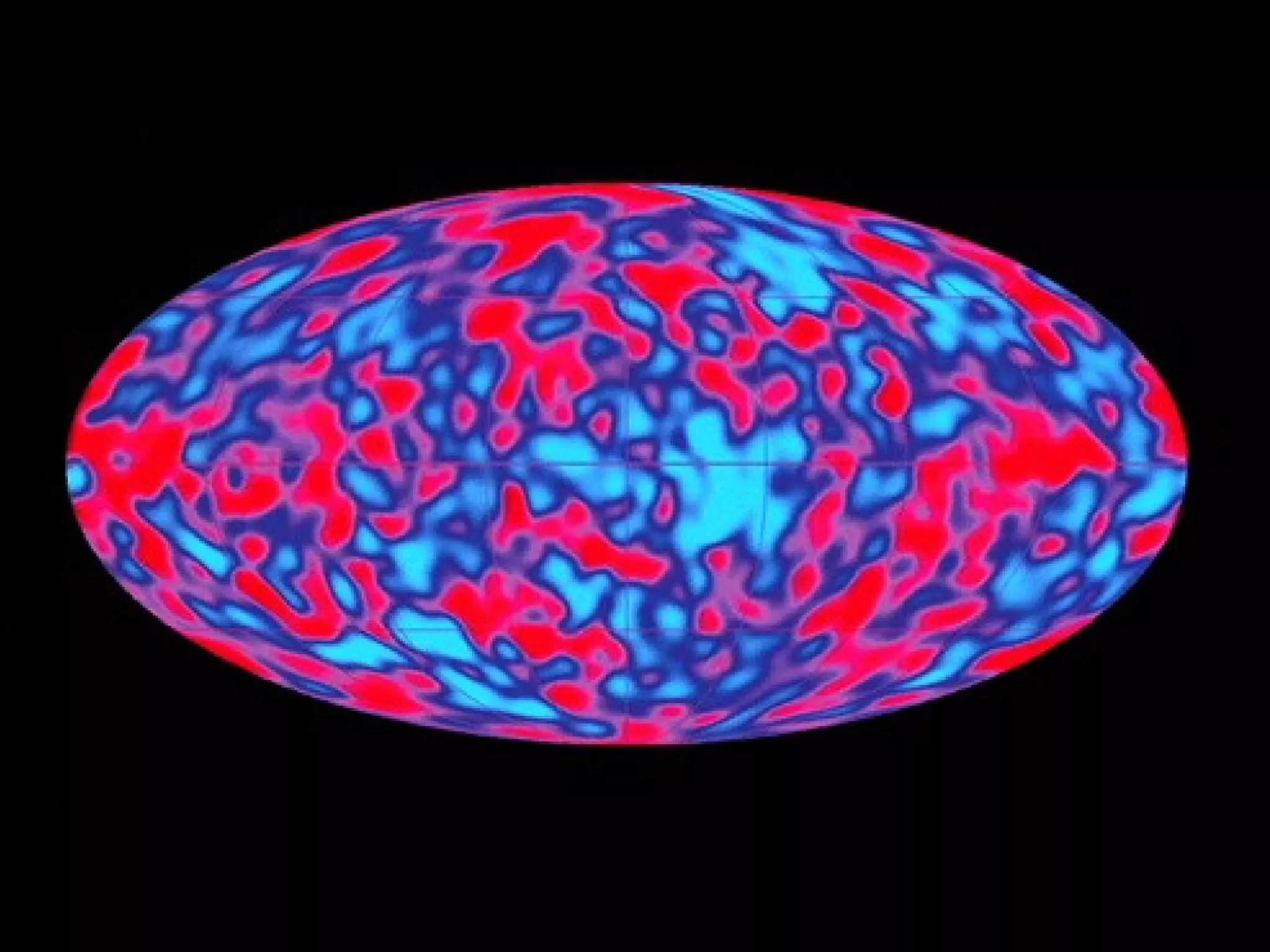
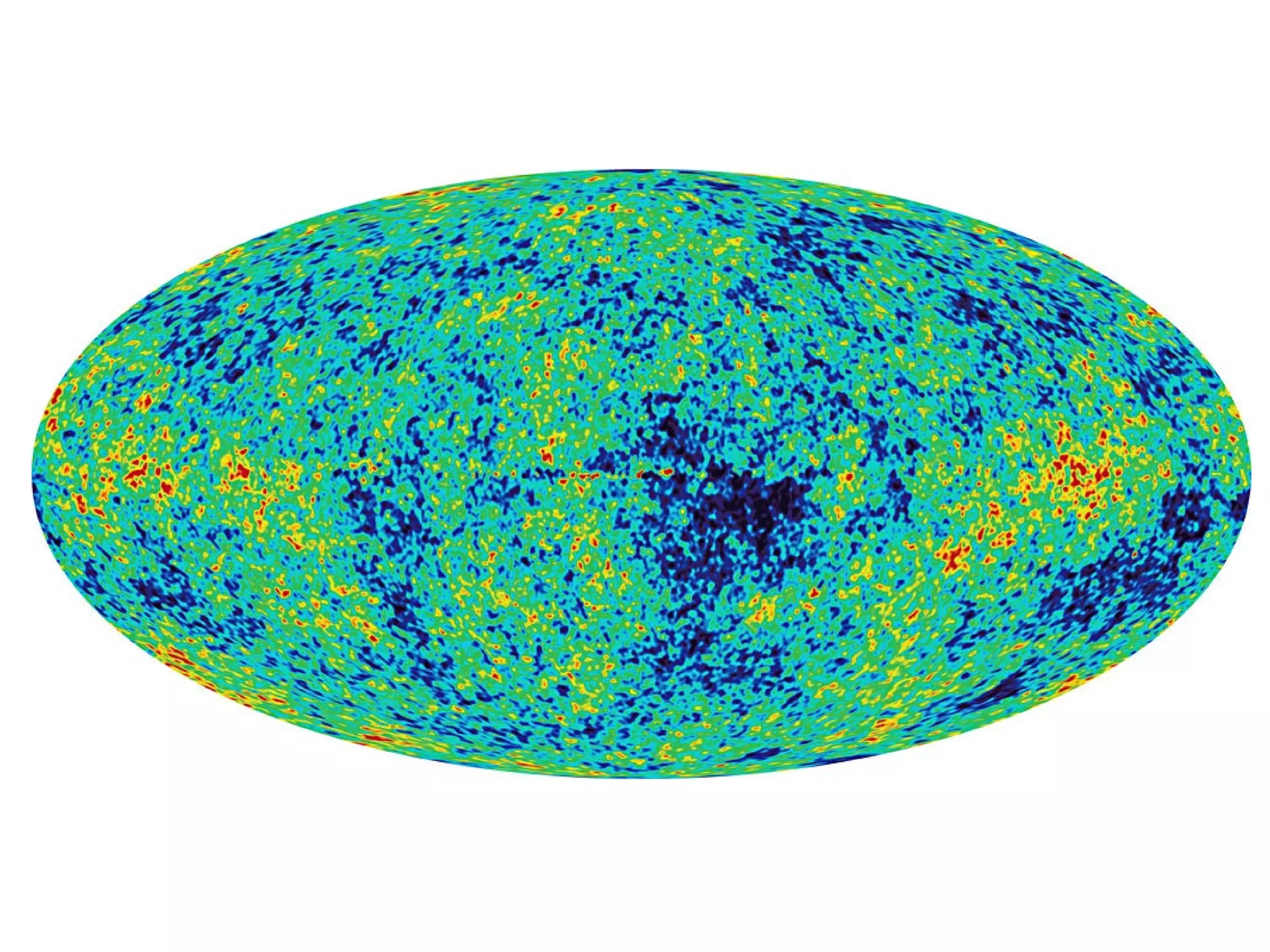
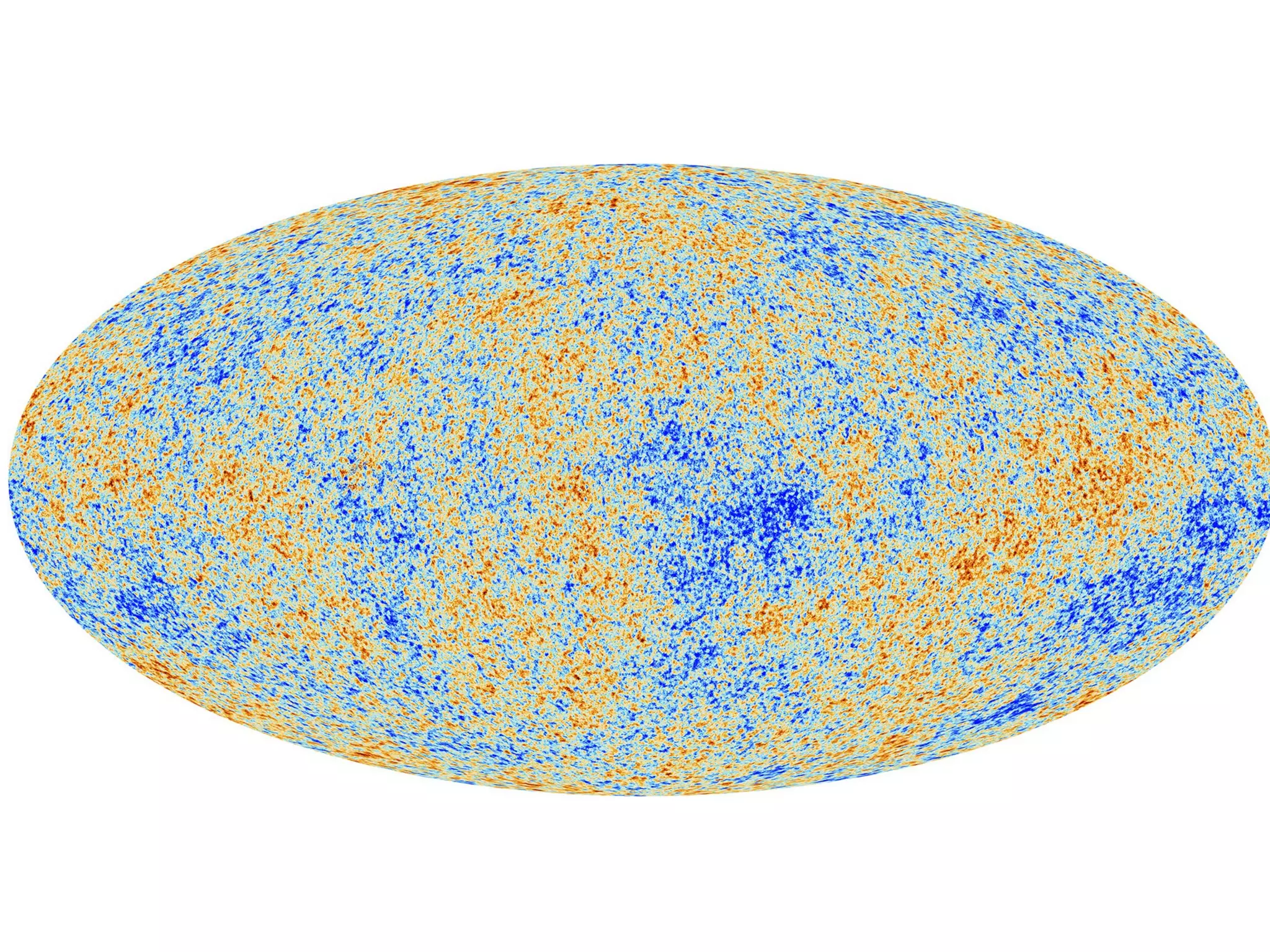
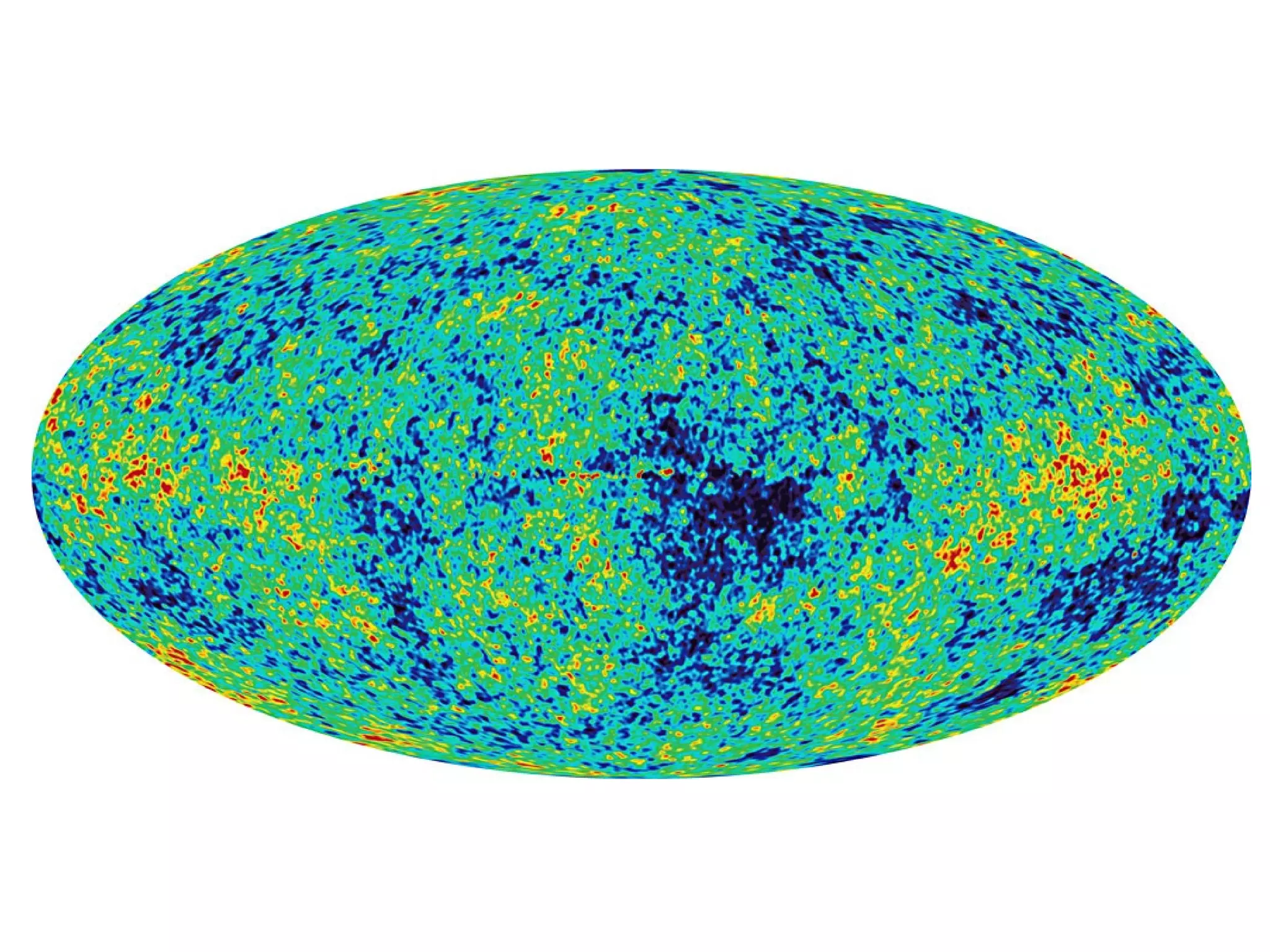
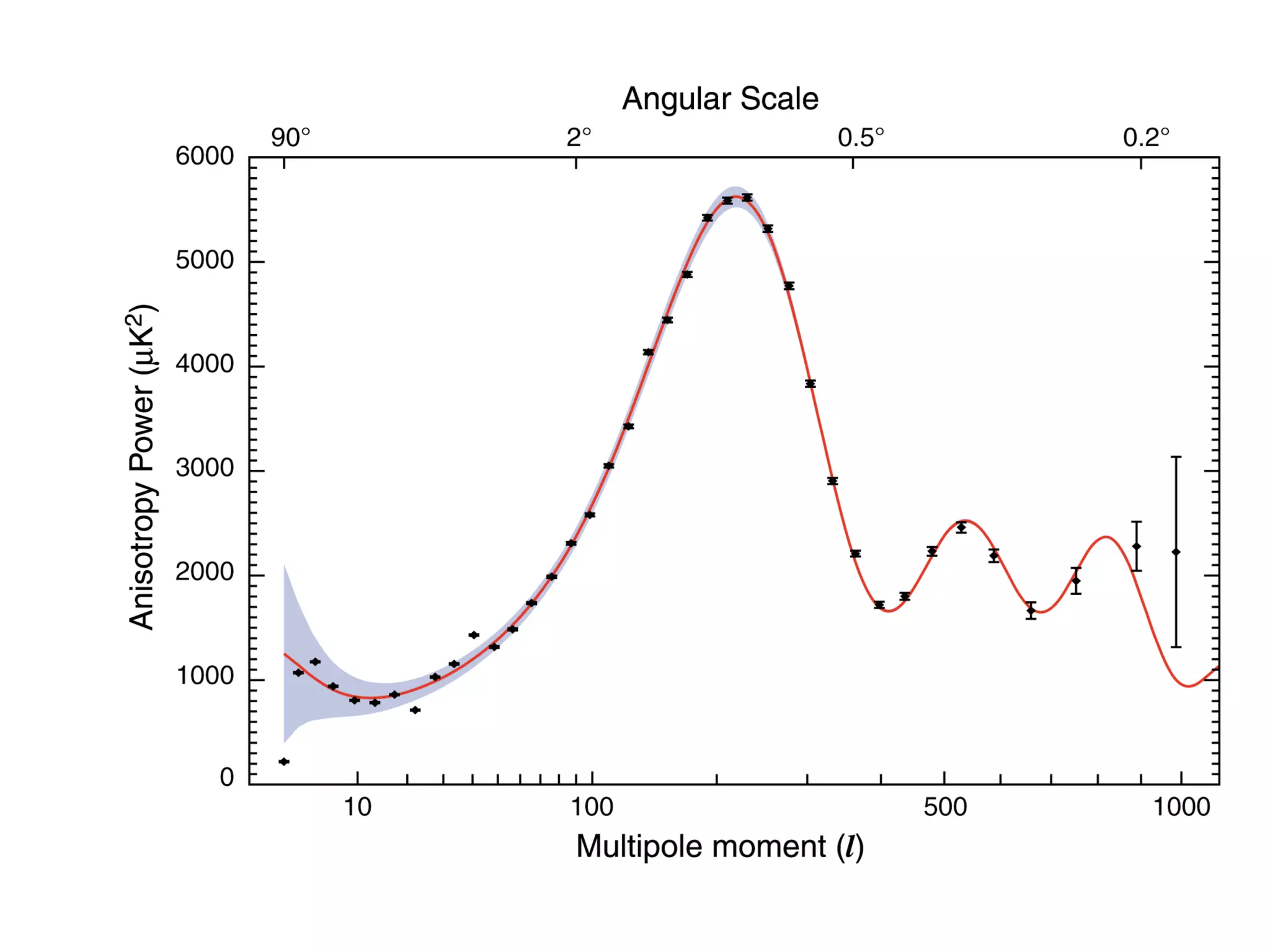
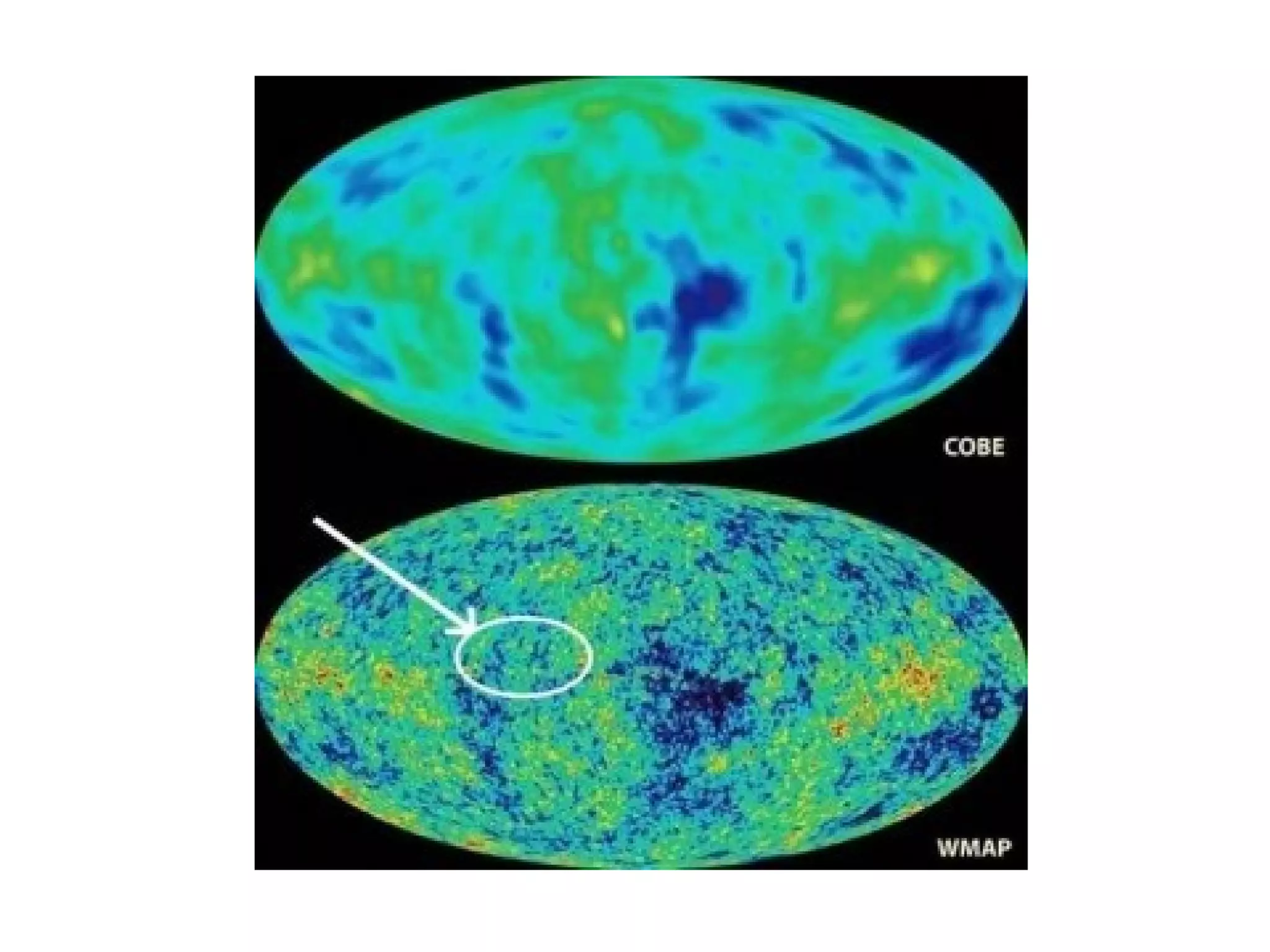
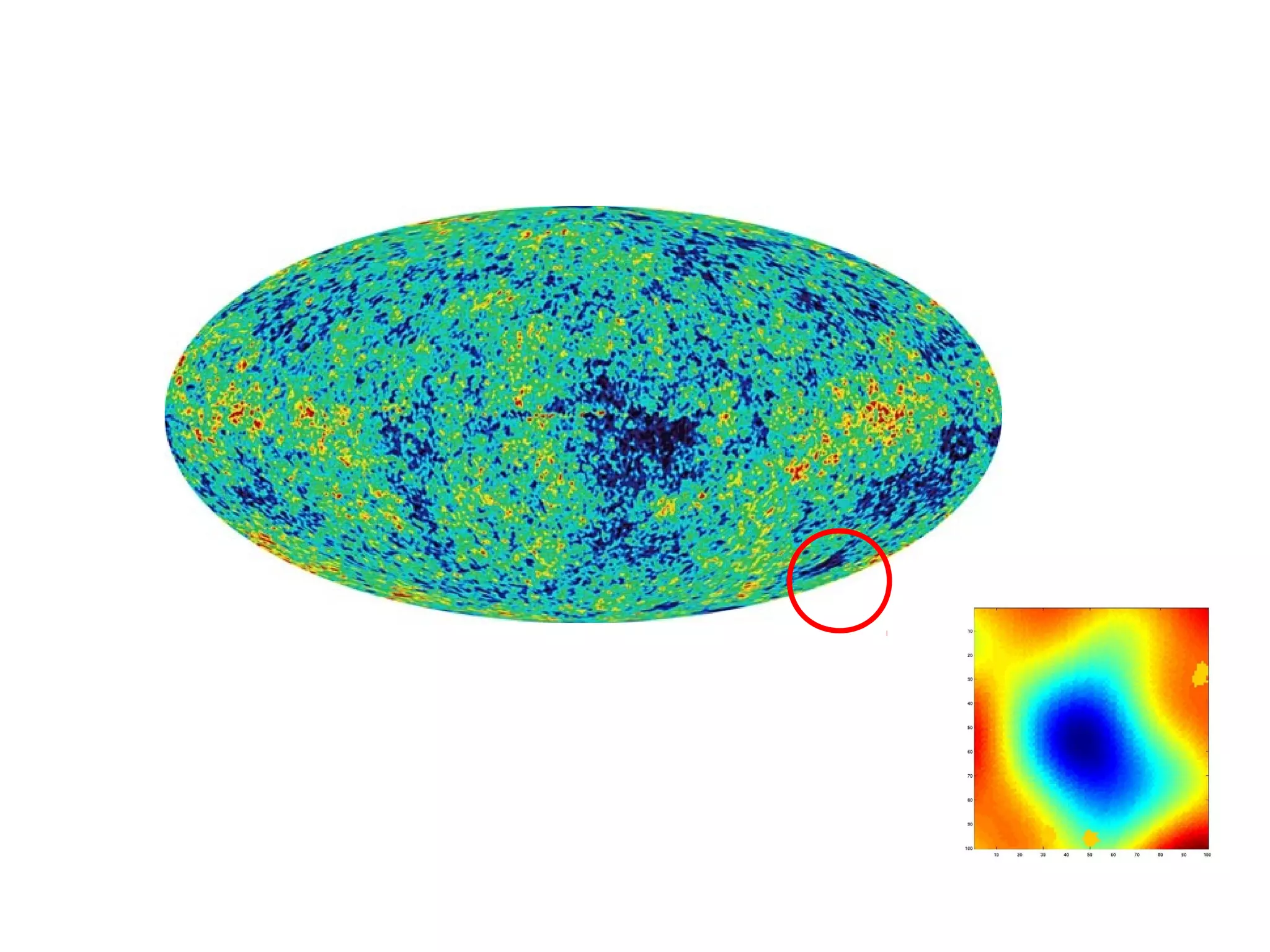
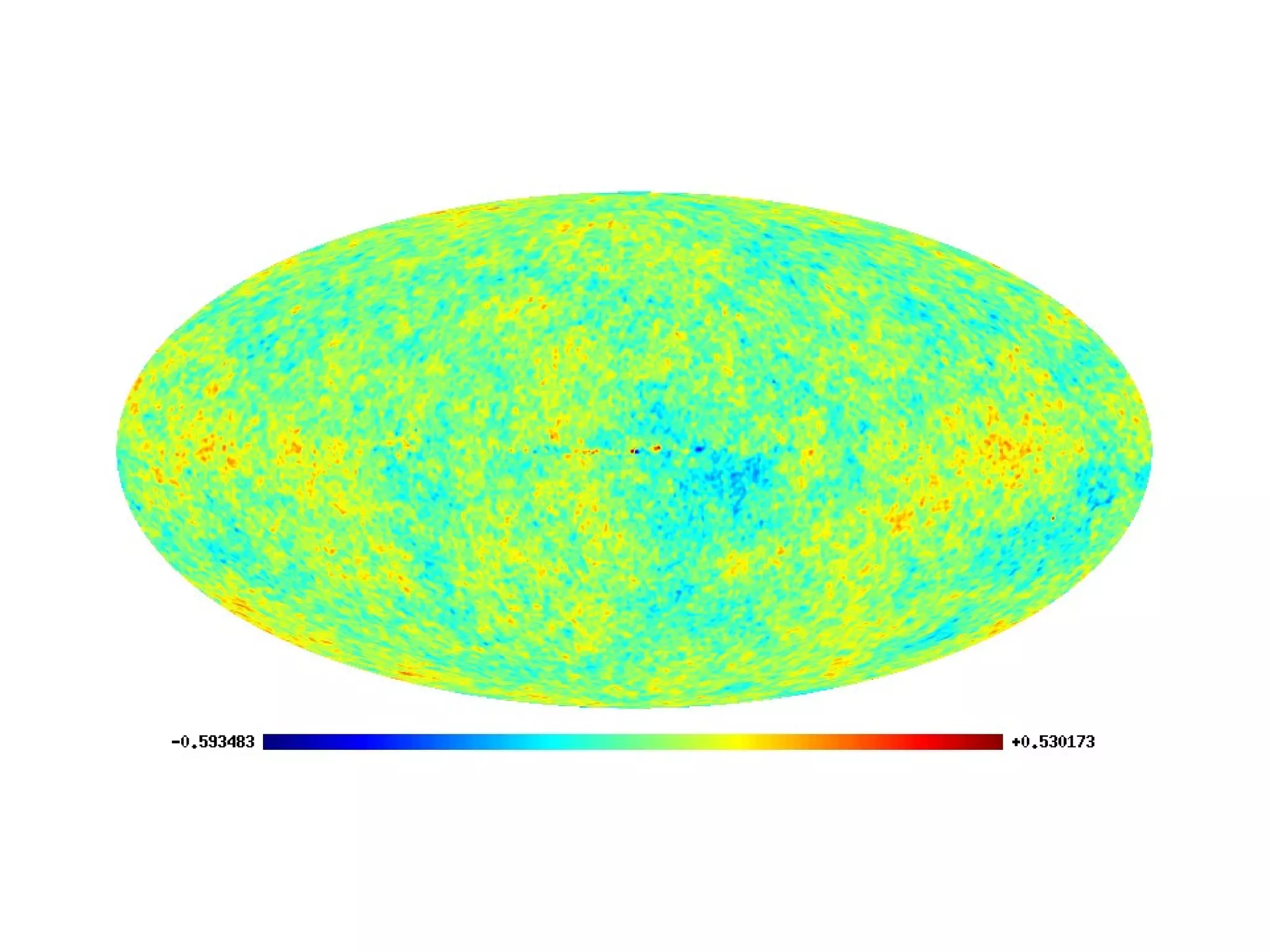
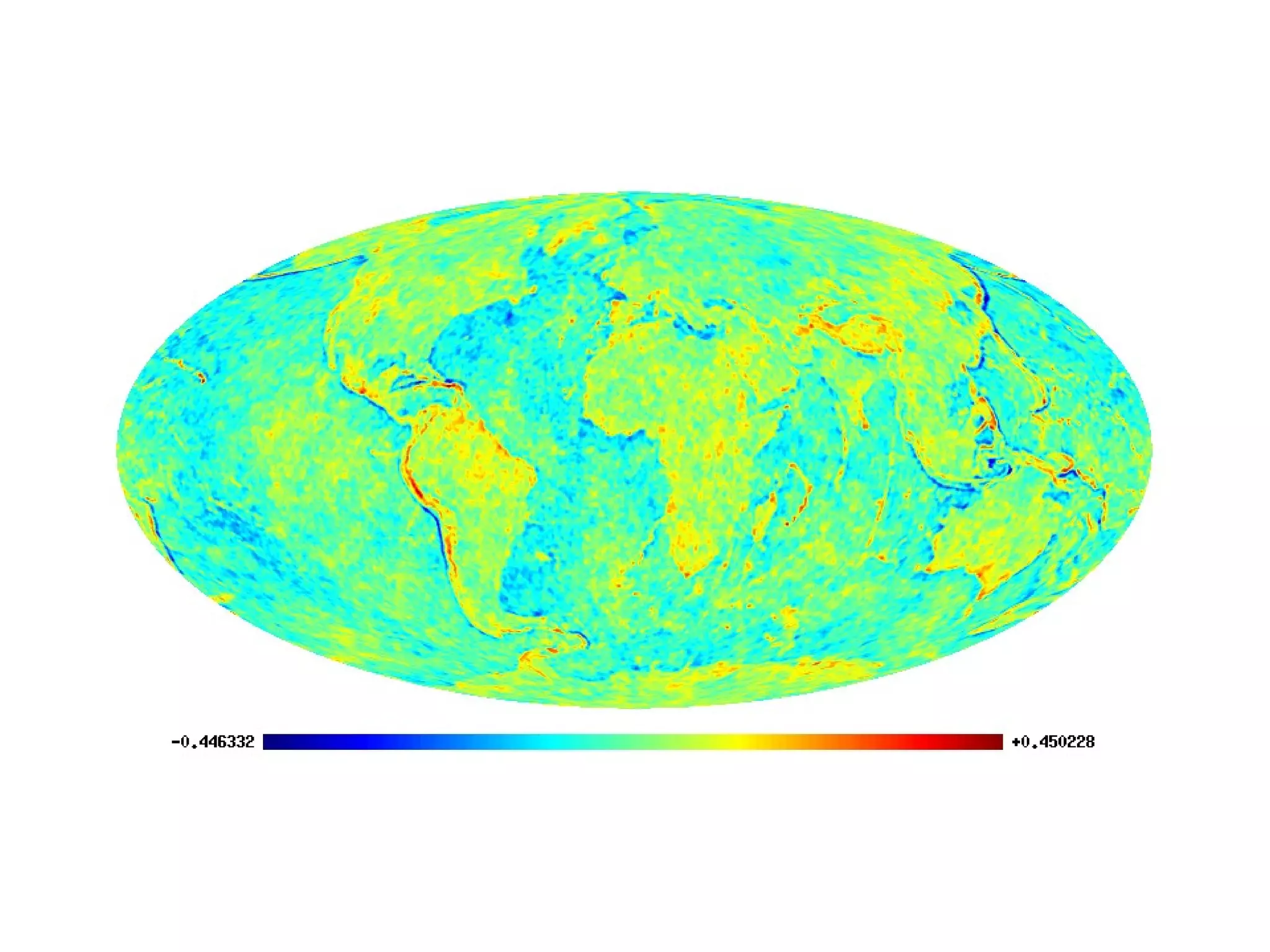
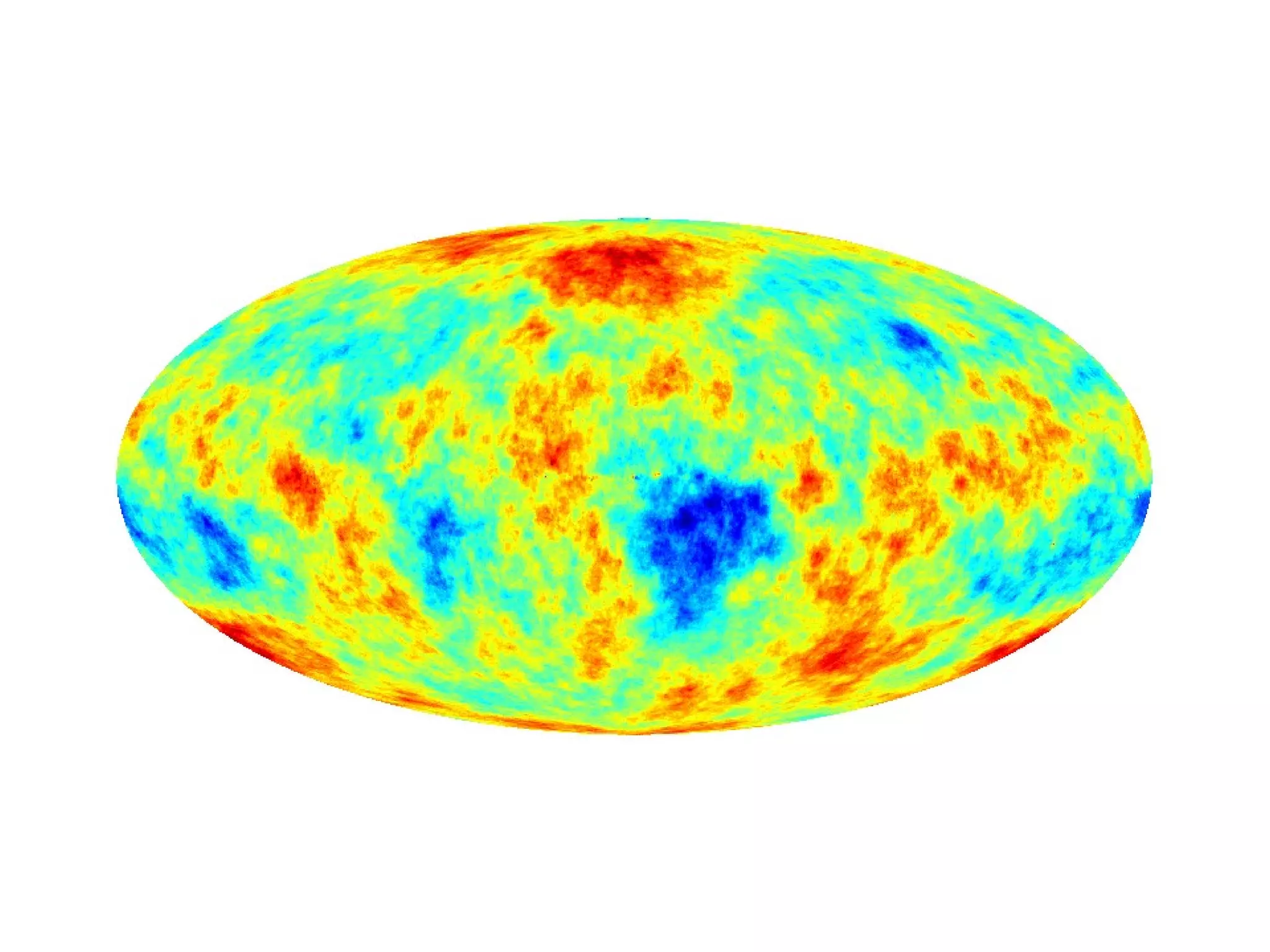
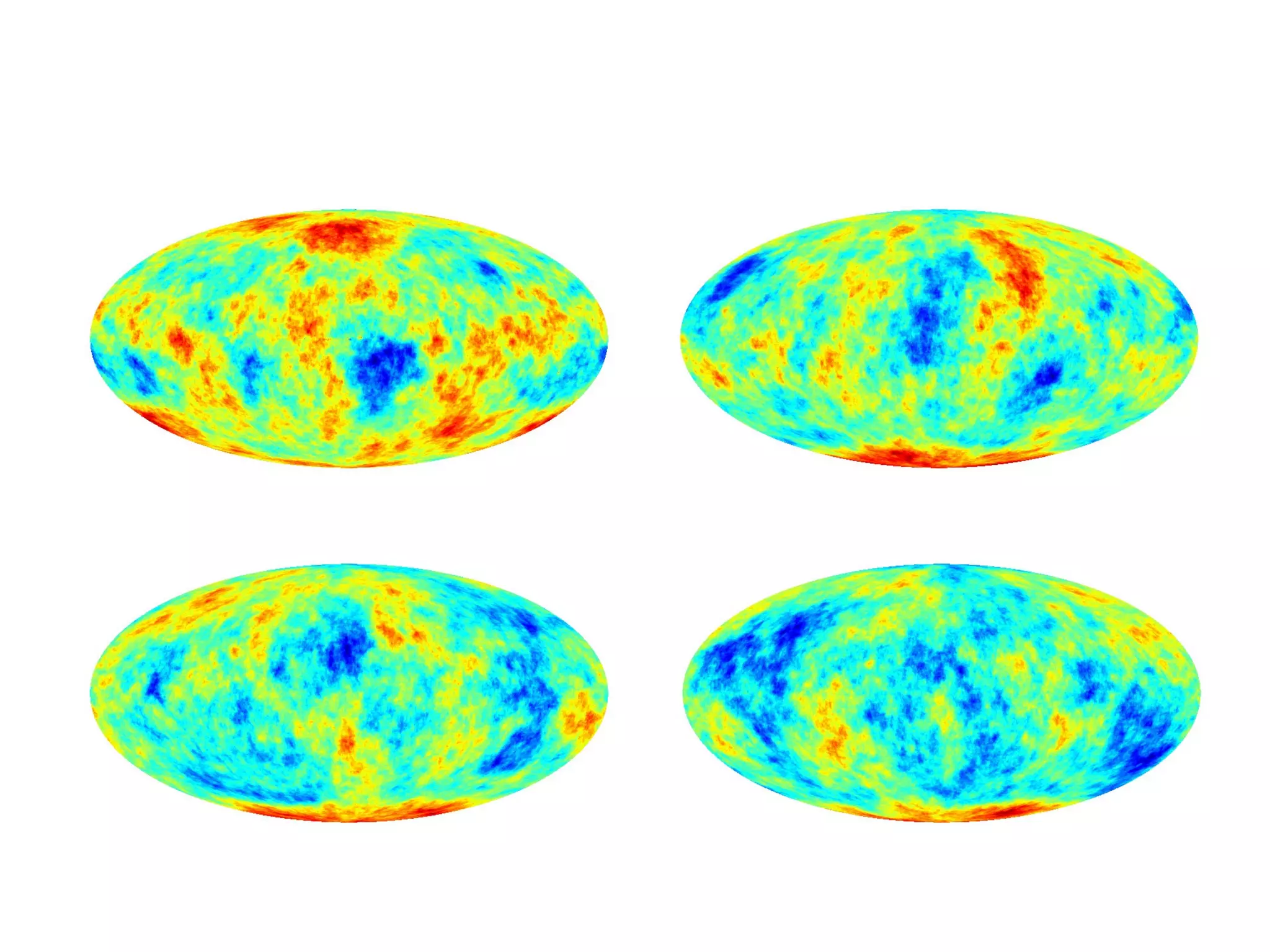
- 28. Weirdness in Phases ΔT(θ,φ ) T =∑∑ al,m Ylm(θ,φ) | | [ ]ml,ml,ml, ia=a φexp For a homogeneous and isotropic Gaussian random field (on the sphere) the phases are independent and uniformly distributed. Non- random phases therefore indicate weirdness..
- 37. Edgeworth Expansion This isuseful for many things, but does not guarantee that the result is a proper probability distribution!
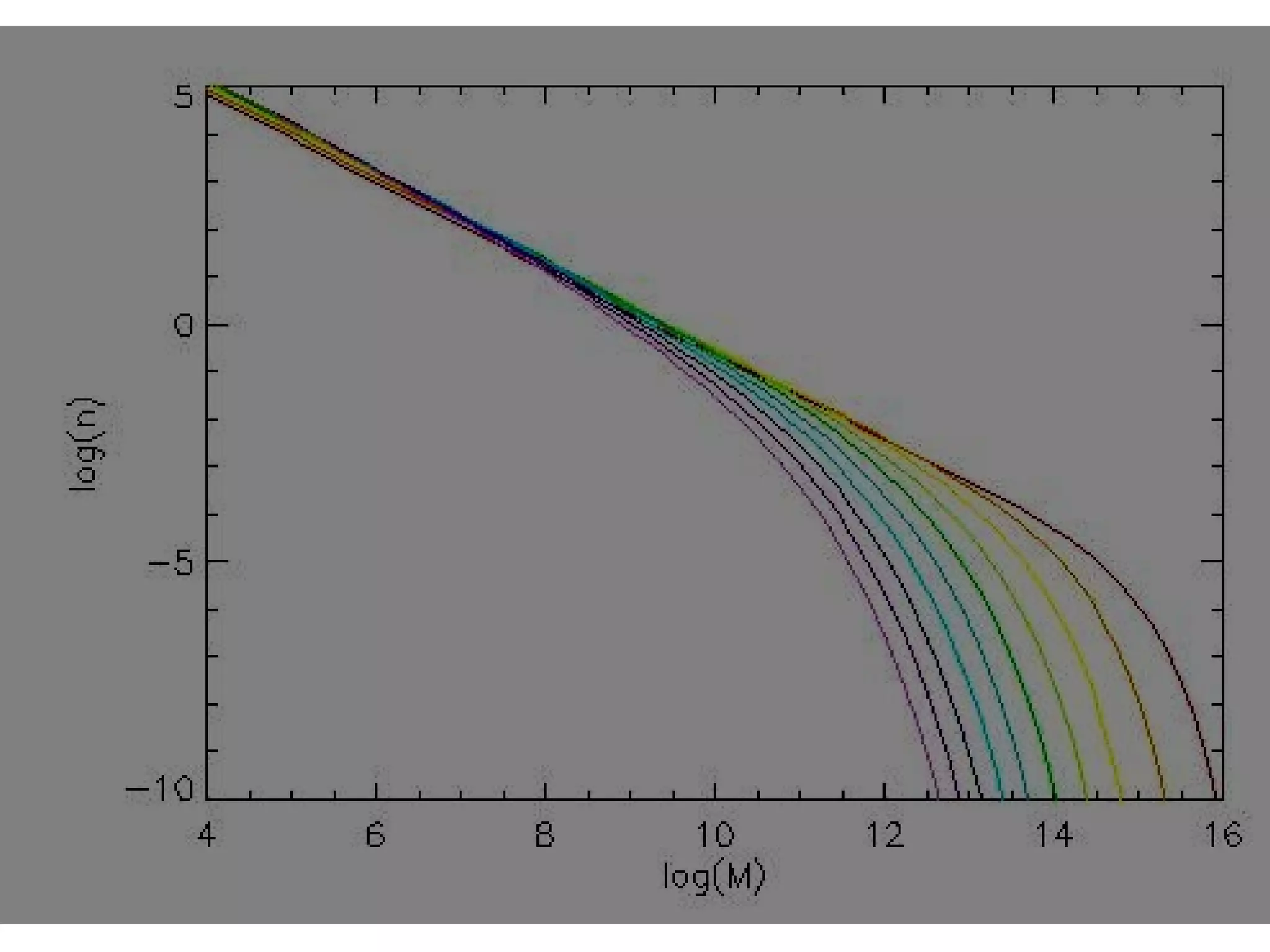
- 38. Extreme Value Statistics (exact) Giventhe distribution of X, what is the distribution of Xmax? [ ] [ ] 1 21max 1max )()()( )( )Pr(.....)Pr()Pr()Pr( ).....sup(:}{ − =⇒ = ≤××≤×≤=≤ = n n n ni zFznfzg zF zXzXzXzX XXXX
- 39. Extreme Value Statistics (asymptotic) Forany distribution of exponential type, in the sense that Then there is a stable asymptotic distribution 0 )( )(1 lim = − ∞→ xf xF dx d x − −−→ ∞→∞→≤ n n a bz zG xaszX expexp)( )Pr( max
- 40.
- 47. Waizman, Ettori & Moscardini,2011 arXiv:1105.4099See also: Colombi et al. 2011; Davis et al. 2011 etc These use alternative parametrisations
- 48. Conclusions • The successof the standard cosmology is very constraining… • But while we may have less freedom than we did 30 years ago, we do have one thing that we didn’t have then: DATA! • Might there be things lurking in data we already have?