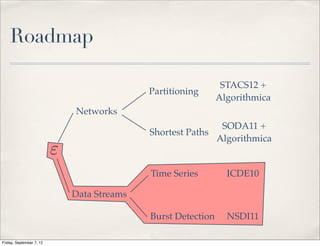
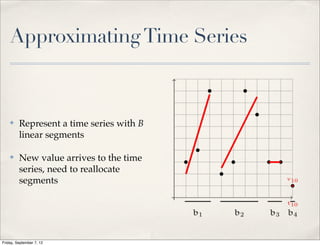
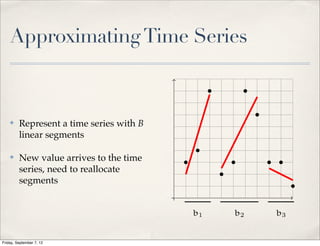
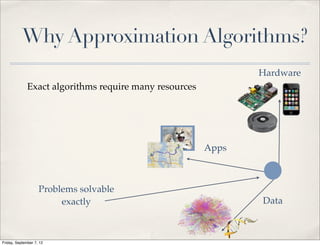
The document summarizes Luca Foschini's Ph.D. defense presentation on approximation algorithms for problems on networks and data streams. The defense committee consisted of Subhash Suri (chair), John Gilbert, and Teofilo Gonzalez. The presentation covered Foschini's work developing approximation algorithms for problems like graph partitioning, shortest paths, time series analysis, and burst detection on data streams and networks. It provided overviews of the algorithms developed and their applications, as well as the time complexities analyzed.











![Motivation & Complexity
✤ Divide-and-conquer algorithms
✤ VLSI design
✤ Parallel computing
✤ NP-hard to approximate cut size within any finite value alpha
[Andreev and Räcke 2006]
Friday, September 7, 12](https://image.slidesharecdn.com/aaabbbbccccc-120907145505-phpapp02/85/Aaabbbbccccc-16-320.jpg)

![General Graphs & Trees
✤ Algorithm is !-approximation if
finds a cut at most ! times optimal
✤ NP-hard to approximate cut size
within any finite ! [Andreev and
Räcke 2006]
Friday, September 7, 12](https://image.slidesharecdn.com/aaabbbbccccc-120907145505-phpapp02/85/Aaabbbbccccc-18-320.jpg)
![General Graphs & Trees
✤ Algorithm is !-approximation if
finds a cut at most ! times optimal
✤ NP-hard to approximate cut size
within any finite ! [Andreev and
Räcke 2006]
Trees - simple instances?
Friday, September 7, 12](https://image.slidesharecdn.com/aaabbbbccccc-120907145505-phpapp02/85/Aaabbbbccccc-19-320.jpg)
![General Graphs & Trees
✤ Algorithm is !-approximation if
finds a cut at most ! times optimal
✤ NP-hard to approximate cut size n=31, k=8 cut size = 10
within any finite ! [Andreev and
Räcke 2006]
Trees - simple instances?
n=31, k=9 cut size = 8
Friday, September 7, 12](https://image.slidesharecdn.com/aaabbbbccccc-120907145505-phpapp02/85/Aaabbbbccccc-20-320.jpg)










![Extension to General Graphs
✤ Decomposition of graph into collection of trees [Räcke, Madry], cut
size worsen by at most O(log n) for at least 1 tree
✤ Apply PTAS for trees to each instance
✤ Return partition for tree with minimum cut
✤ alpha = O(log n) improves
Friday, September 7, 12](https://image.slidesharecdn.com/aaabbbbccccc-120907145505-phpapp02/85/Aaabbbbccccc-32-320.jpg)