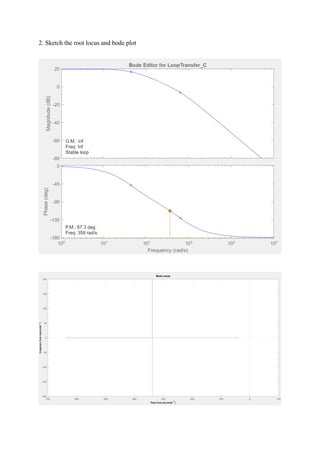
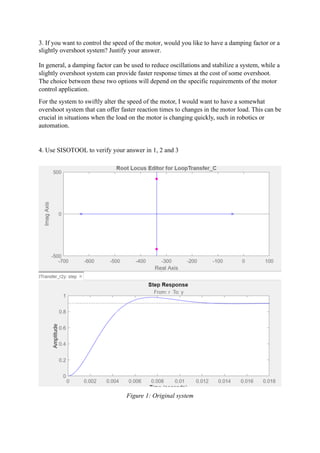
This document is an assignment for a control system design course. It contains questions regarding the modeling and analysis of a motor system using Laplace transforms. Specifically, it asks the student to: 1) Derive the transfer function for the motor system. 2) Sketch the root locus and Bode plot. 3) Justify whether a damping factor or overshoot system would be preferred for motor speed control and why. 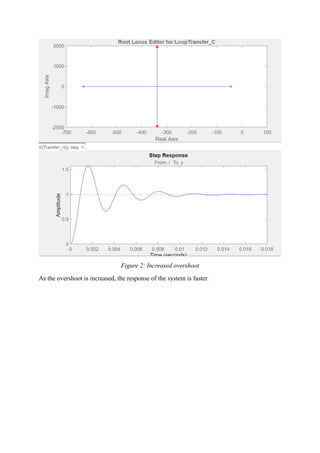4) Use MATLAB/Simulink to verify the answers.

1. COURSE
KKKZ 4123 CONTROL SYSTEM DESIGN
SEMESTER 1 2022/2023
SET 2
TITLE
ASSIGNMENT 2
LECTURER
EN. HILMI BIN SANUSI
NAME
GURPREET SINGH A/L HARBANS SINGH (A174738)

2. question I
Ta(s)=
Kaia (s) -
D
Tr(s)
=
JmsPOCs) + Bm8(s)
=
T
a(s) -
T.(S)
Sms0(s) +
BmsO(s) =
Ta(s) -
B
Va(s) =
iaRa(s) +
LaSia(s) +
Ua(s) -
Ua(s) =
VaS8(s) -
Compare D and D
kaia(s)
=
JmsOCs) +
BmS8(s)
ia(s) =
CmSOCs) +
BmsO(s) -
B
Ka
Uq(s) =
(Ra+LaS)
i
q(s) +
Up(s) -
equation & rewritten
Sub in
equation &
and I
"a(S) =
(RatLaSS
(ImsItBms)
8cs) +
Ras
Ua(s) =
(PatLas)(Ims'+BmS] ha-
b(s)
ha
Let
0 (s) =
Wr(S)
Macha - sub values
(a+LaS)(3ms+
BmS)+ kaz
Ua() =
0.105
W.Cs)(2.7+0.004s)(0000s+00000093) +
(0.10))2
0.185
=
(4x(-7)5 +
(2.7x10-4)s +
0.011025

3. 2. Sketch the root locus and bode plot

4. 3. If you want to control the speed of the motor, would you like to have a damping factor or a
slightly overshoot system? Justify your answer.
In general, a damping factor can be used to reduce oscillations and stabilize a system, while a
slightly overshoot system can provide faster response times at the cost of some overshoot.
The choice between these two options will depend on the specific requirements of the motor
control application.
For the system to swiftly alter the speed of the motor, I would want to have a somewhat
overshoot system that can offer faster reaction times to changes in the motor load. This can be
crucial in situations when the load on the motor is changing quickly, such in robotics or
automation.
4. Use SISOTOOL to verify your answer in 1, 2 and 3
Figure 1: Original system

5. Figure 2: Increased overshoot
As the overshoot is increased, the response of the system is faster.