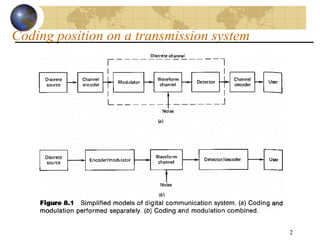
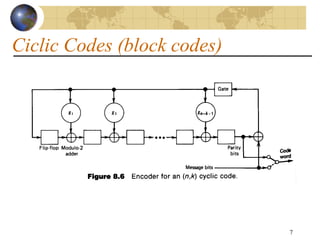
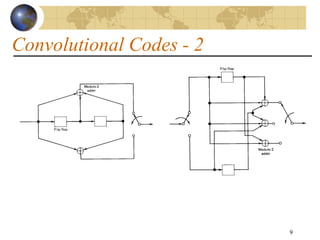
This document discusses error detection and correction techniques used in digital communications. It describes three main types of error coding: parity bits for error detection, block coding for error detection and correction (e.g. Reed-Solomon), and convolutional coding for error correction (e.g. Viterbi). It provides details on parity bits, block codes including cyclic codes, and convolutional codes. Formulas for coding gain, data rates, required signal-to-noise ratios, and bit error rate calculations as a function of modulation scheme and energy per bit to noise spectral density ratio are also summarized.

1. 1
Error Detection and Correction

2. 2
Coding position on a transmission system

3. 3
Error Protection Coding
Three types to discuss
Parity Bits (error detection only, really a subset of BC)
Block Coding (eg. Reed-Solomon)
Convolutional Coding (eg. Viterbi or Turbo)
All impose an overhead on channel
Additional information must be transmitted
This additional information is the redundant information of
the error coding
Block codes develop less coding gain but are (much)
easier to process (esp. at high data rates)
Often advantageous to use both together
Gain depends on BER - must be careful here
Coding ~ necessary for non-lin. ch.s (discuss BER
flare)
Forward Error
Correction codes

4. 4
Parity Bits
The data is parsed into uniform k-bit words
7 bits is a common data length
An extra bit is added to this to make an k+1
bit transmission word
The value of the k+1th bit is determined by:
Even parity:
Odd parity:
Doesn’t correct errors just detects, and only
an odd number of errors (discuss why)
k
k
k
k
bit
bit
bit
bit
bit
bit
bit
bit












2
1
1
2
1
1

5. 5
Block Codes - 1
The data is parsed into uniform k-bit blocks
Coder adds n-k unique redundant bits
An n-bit block is transmitted
Coder is memoryless - only this block used
Transmitted data rate is then:
Redundant bits used to correct errors
k
n
R
R b
c 

6. 6
Block Codes - 2
Hamming, Golay, BCH, Reed-Solomon, maximal-
length are different types of block codes
Important for this class
Depending on amount of redundancy added, block codes
may be used to detect only or to actually correct bit errors.
Block codes correct burst errors (ie. adjacent errors) as well
as they do random errors.
Not as powerful as convolutional
k
n
R
R b
c 

7. 7
Ciclic Codes (block codes)
r
R
R b
c
1


8. 8
Convolutional Codes - 1
Process as sliding window of data
Use constraint length of k (window length)
Transmit at rate of where r is rate
Fairly high coding gain
Turbo codes are even higher (but harder)
Do not handle burst errors well
r
R
R b
c
1

r=1/3 r=1/2 r=2/3 r=3/4
Eb/No
uncoded
(dB)
BER
k=7 k=8 k=5 k=6 k=7 k=6 k=8 k=6 k=9
6.8 10-3
4.2 4.4 3.3 3.5 3.8 2.9 3.1 2.6 2.6
9.6 10-5
5.7 5.9 4.3 4.6 5.1 4.2 4.6 3.6 4.2
11.3 10-7
6.2 6.5 4.9 5.3 5.8 4.7 5.2 3.9 4.8
infinite 0 7.0 7.3 5.4 6.0 7.0 5.2 6.7 4.8 5.7
Coding Gain (dB) for various Viterbi codes

9. 9
Convolutional Codes - 2

10. 10
Trellis Coding - 1

11. 11
Trellis Coding - 2

12. 12
Interleaving and Code on Code
Problem: Noise often happens in bursts
Can use interleaving - spreading adjacent bits
of convolutional code over time to avoid
having adjacent bits corrupted
But, we still have a quandary:
Block codes are robust against bursts
Convolutional codes provide more gain
Solution: use both inner convolutional and
outer block codes to get both effects

13. 13
Summary of Useful Formulas

14. 14
Summary of Digital Communications -1
Bw = Bandwidth in Hertz
 = Roll-off factor (from 0 to 1)
Gc = Coding Gain (convert from dB to linear to use in formulas)
Ov = Channel Overhead (convert from % to fraction : 0 to1)
M = modulation size. (Ex: 2, 4, 16, 64)
Legend of variables mentioned in this section:
BER = Bit Error Rate

15. 15
Summary of Digital Communications - 2
• Bits per Symbol: M
Log
Bs 2

• Symbol Rate [symbol/second]: W
s B
R



1
1
• Gross Bit Rate [bps]: W
s
s
G B
M
Log
R
B
R 









1
1
2
• Net Data Rate [bps]:
)
1
(
1
1
)
1
( 2 Ov
B
M
Log
Ov
R
R W
G
i 












16. 16
Summary of Digital Communications - 3
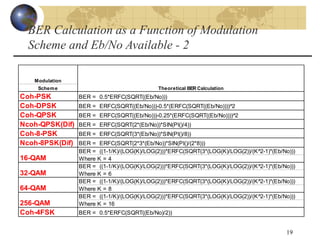
• Required Eb/No (assuming no coding) [adimensional]:
(function of modulation scheme and required bit error rate – see table later)
BER)
Scheme,
n
(Modulatio
function
Table 1
theory
from
Req
0










N
Eb
• Required Eb/No (using coding gain) [adimensional]:
theory
from
Req
0
Re
0
1

















N
E
G
N
E b
c
q
b
• Required C/N [adimensional]:
W
G
q
b
q B
R
N
E
N
C
*
Re
0
Re
















17. 17
Summary of Digital Communications - 4
• Required Signal Strength [Watts]:
Where k = Boltzman constant = 1.38e-23 J/Hz
TS = System Noise Temperature
T0 = ambient temperature (usually 290 K)
F = System Noise figure in linear scale (not in dB)
F
B
kT
N
C
B
kT
N
C
N
N
C
C
W
q
W
s
q
q
q
0
Re
Re
Re
Re






















18. 18
BER Calculation as a Function of Modulation
Scheme and Eb/No Available
• Equations given on next slide are used to calculate the bit error
rate (BER) given the bit energy by spectral noise ratio (Eb/No) as
input.
• These functions are used in their direct form for the bit error rate
calculations. Excel and some scientific calculators provide the
solution for the “erfc” function.
• The formulas provided can be inverted by numerical methods to
obtain the Eb/No required as a function of the BER.
• Also possible to draw the graphic and obtain the “inverse” by
graphical inspection.

19. 19
BER Calculation as a Function of Modulation
Scheme and Eb/No Available - 2
Modulation
Scheme
Coh-PSK BER = 0.5*ERFC(SQRT((Eb/No)))
Coh-DPSK BER = ERFC(SQRT((Eb/No)))-0.5*(ERFC(SQRT((Eb/No))))^2
Coh-QPSK BER = ERFC(SQRT((Eb/No)))-0.25*(ERFC(SQRT((Eb/No))))^2
Ncoh-QPSK(Dif) BER = ERFC(SQRT(2*(Eb/No))*SIN(PI()/4))
Coh-8-PSK BER = ERFC(SQRT(3*(Eb/No))*SIN(PI()/8))
Ncoh-8PSK(Dif) BER = ERFC(SQRT(2*3*(Eb/No))*SIN(PI()/(2*8)))
BER = ((1-1/K)/(LOG(K)/LOG(2)))*ERFC(SQRT(3*(LOG(K)/LOG(2))/(K^2-1)*(Eb/No)))
Where K = 4
BER = ((1-1/K)/(LOG(K)/LOG(2)))*ERFC(SQRT(3*(LOG(K)/LOG(2))/(K^2-1)*(Eb/No)))
Where K = 6
BER = ((1-1/K)/(LOG(K)/LOG(2)))*ERFC(SQRT(3*(LOG(K)/LOG(2))/(K^2-1)*(Eb/No)))
Where K = 8
BER = ((1-1/K)/(LOG(K)/LOG(2)))*ERFC(SQRT(3*(LOG(K)/LOG(2))/(K^2-1)*(Eb/No)))
Where K = 16
Coh-4FSK BER = 0.5*ERFC(SQRT((Eb/No)/2))
256-QAM
32-QAM
64-QAM
Theoretical BER Calculation
16-QAM