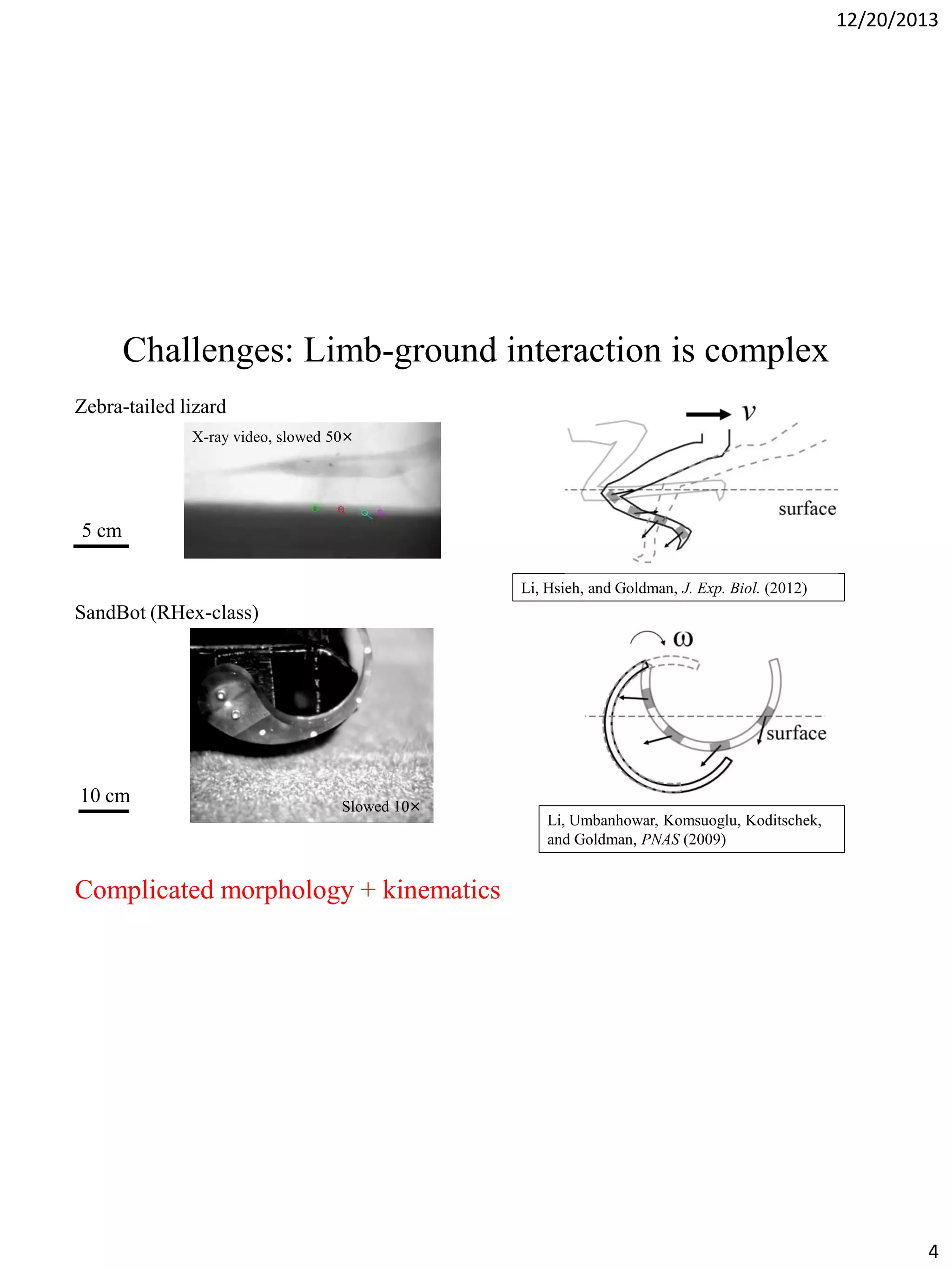
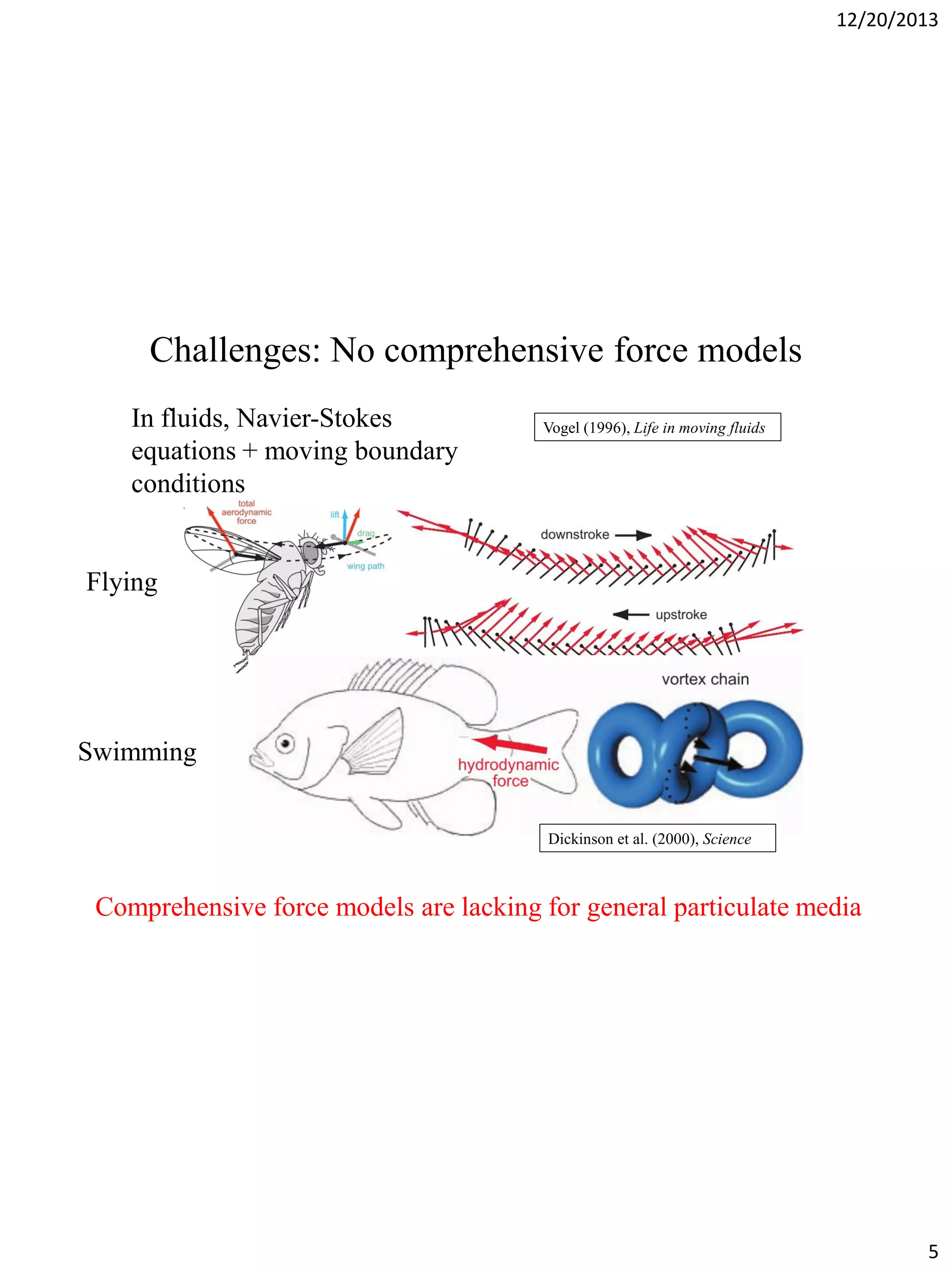
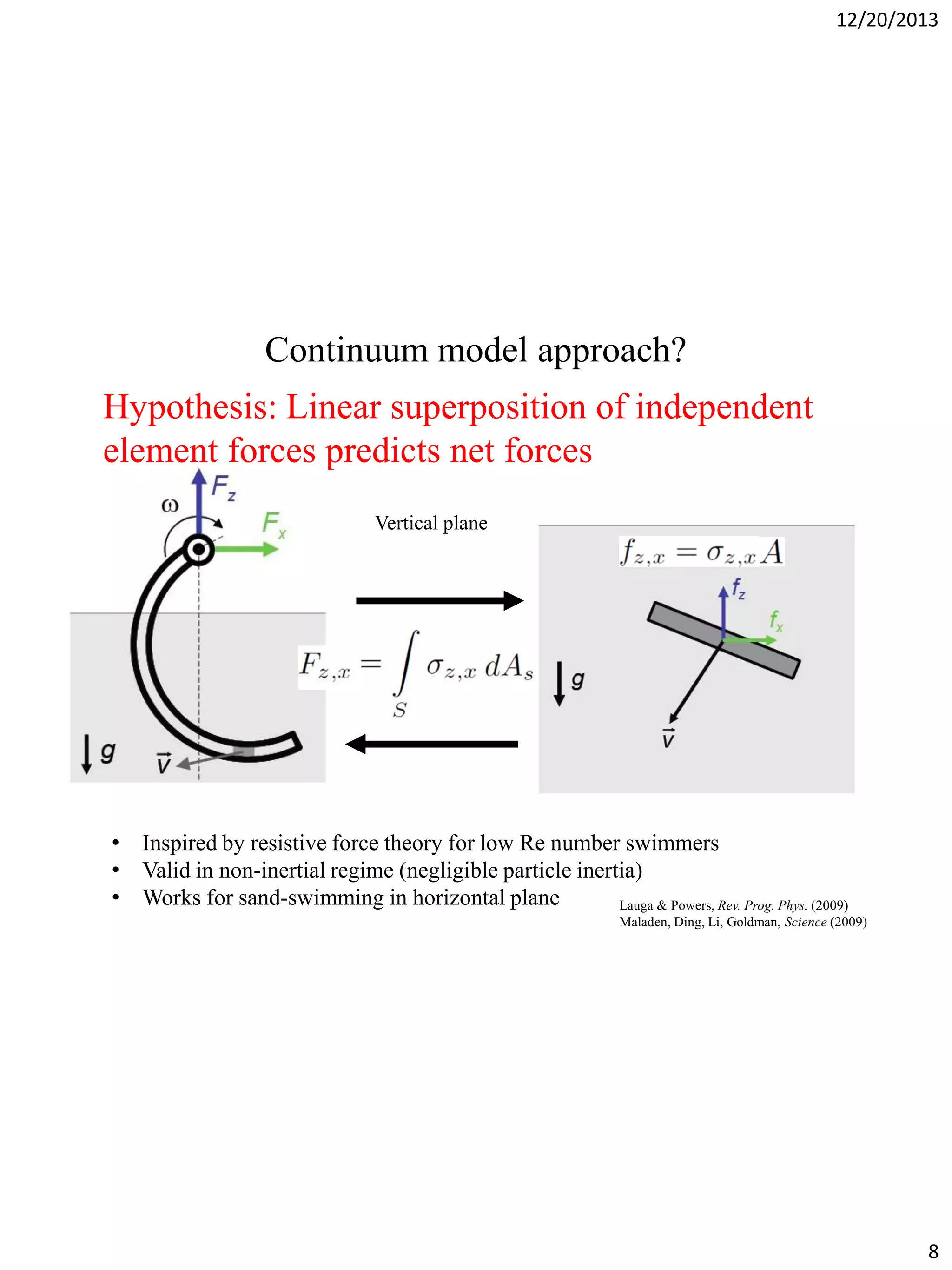
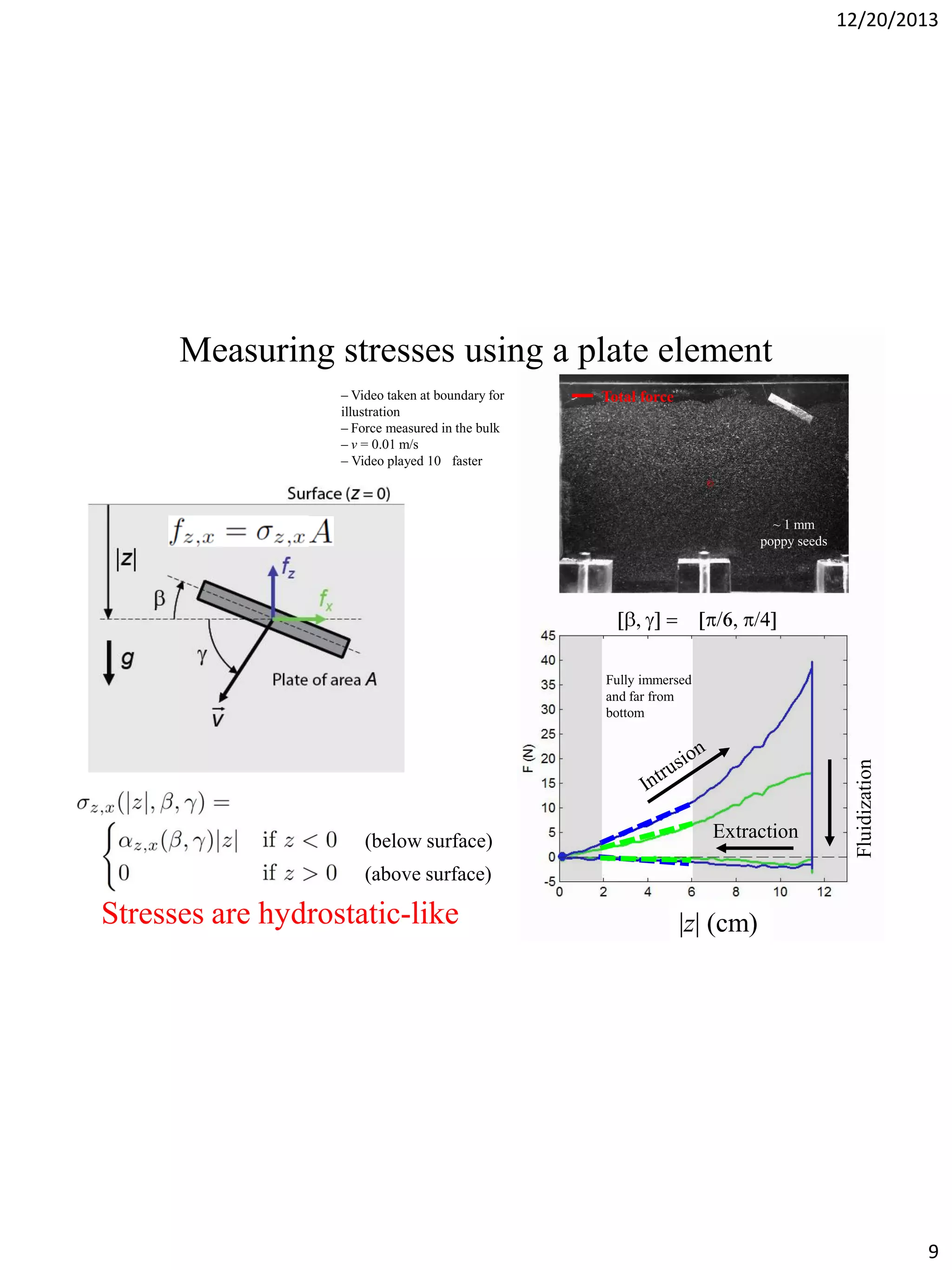
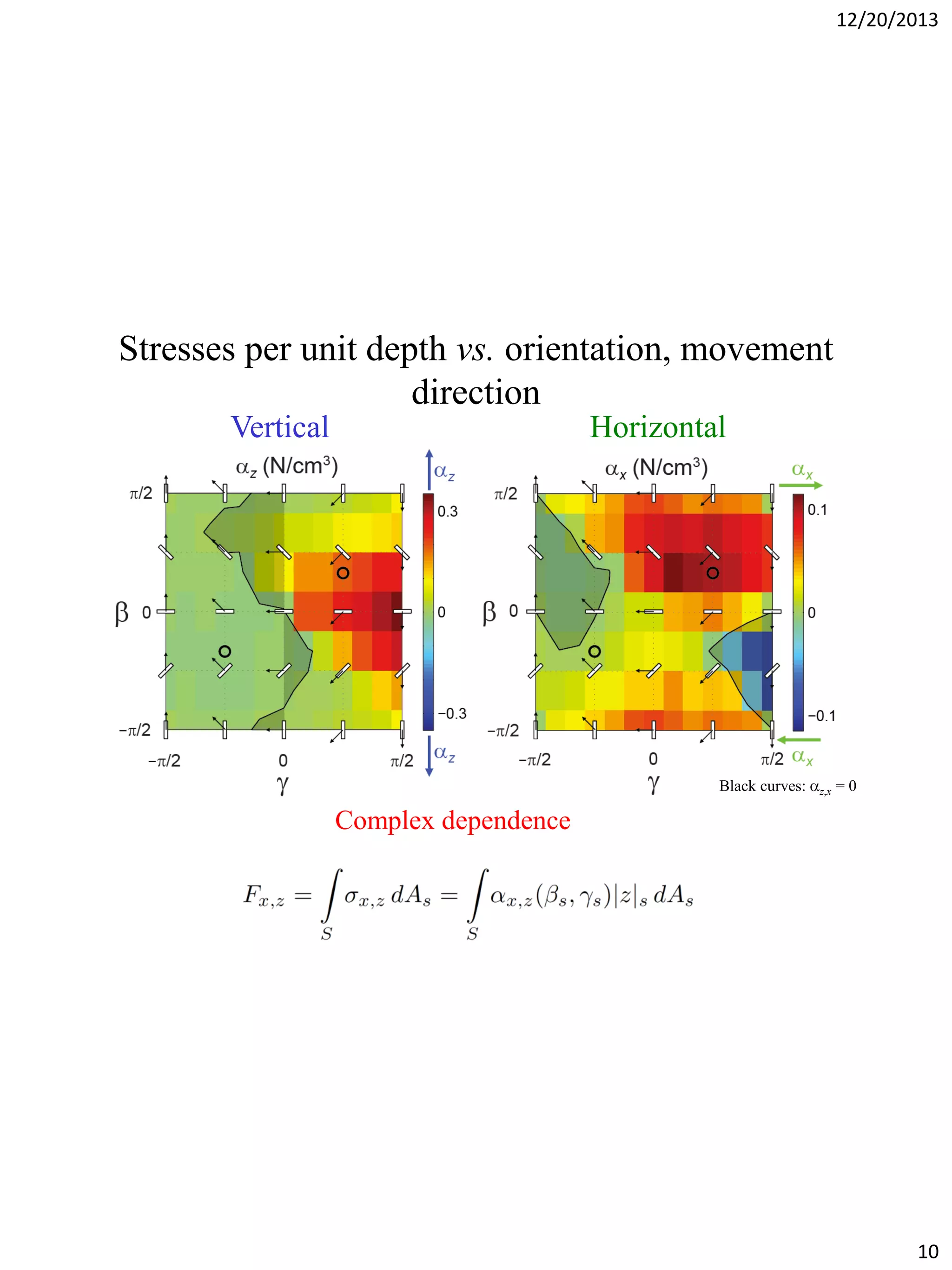
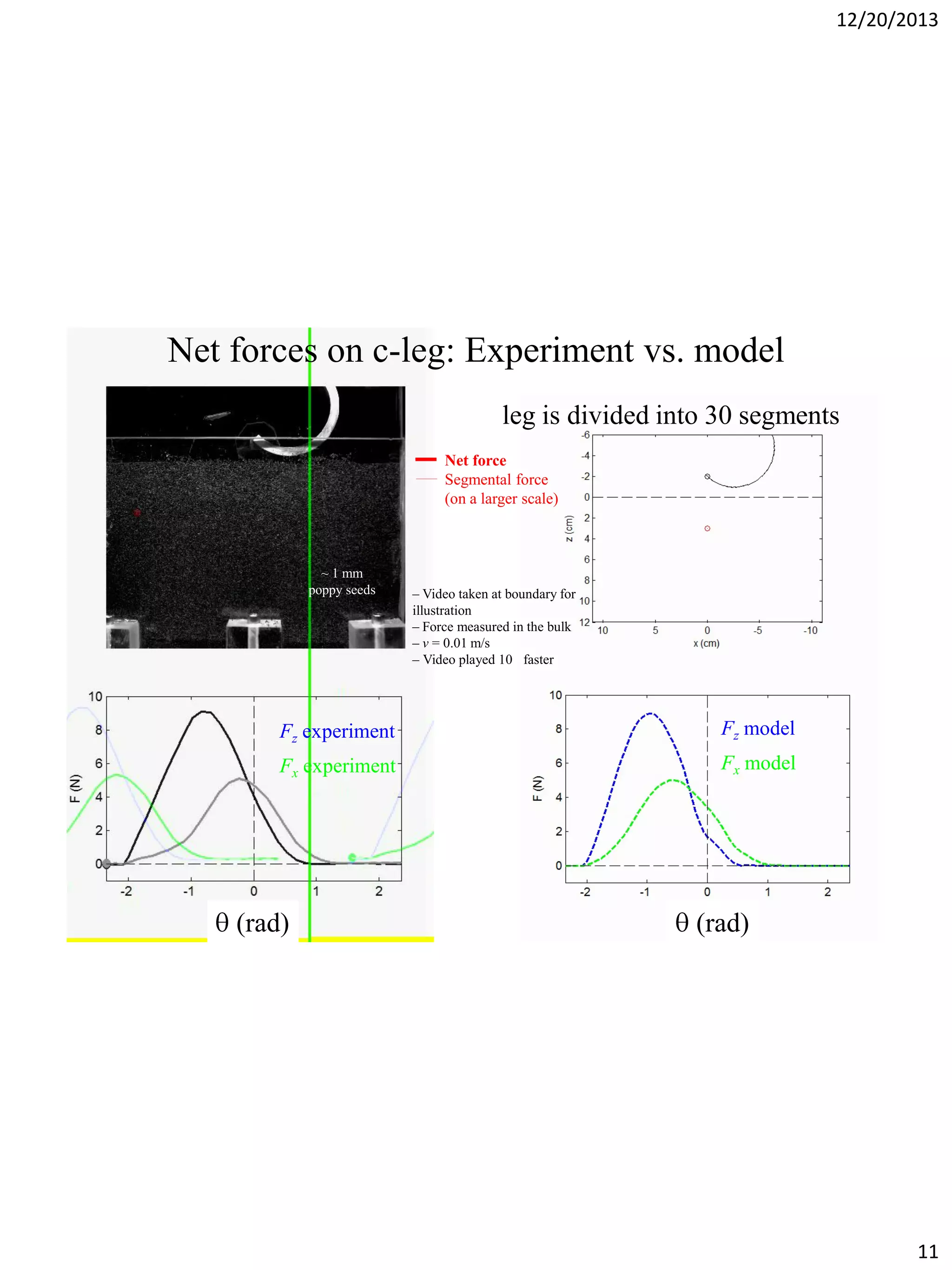
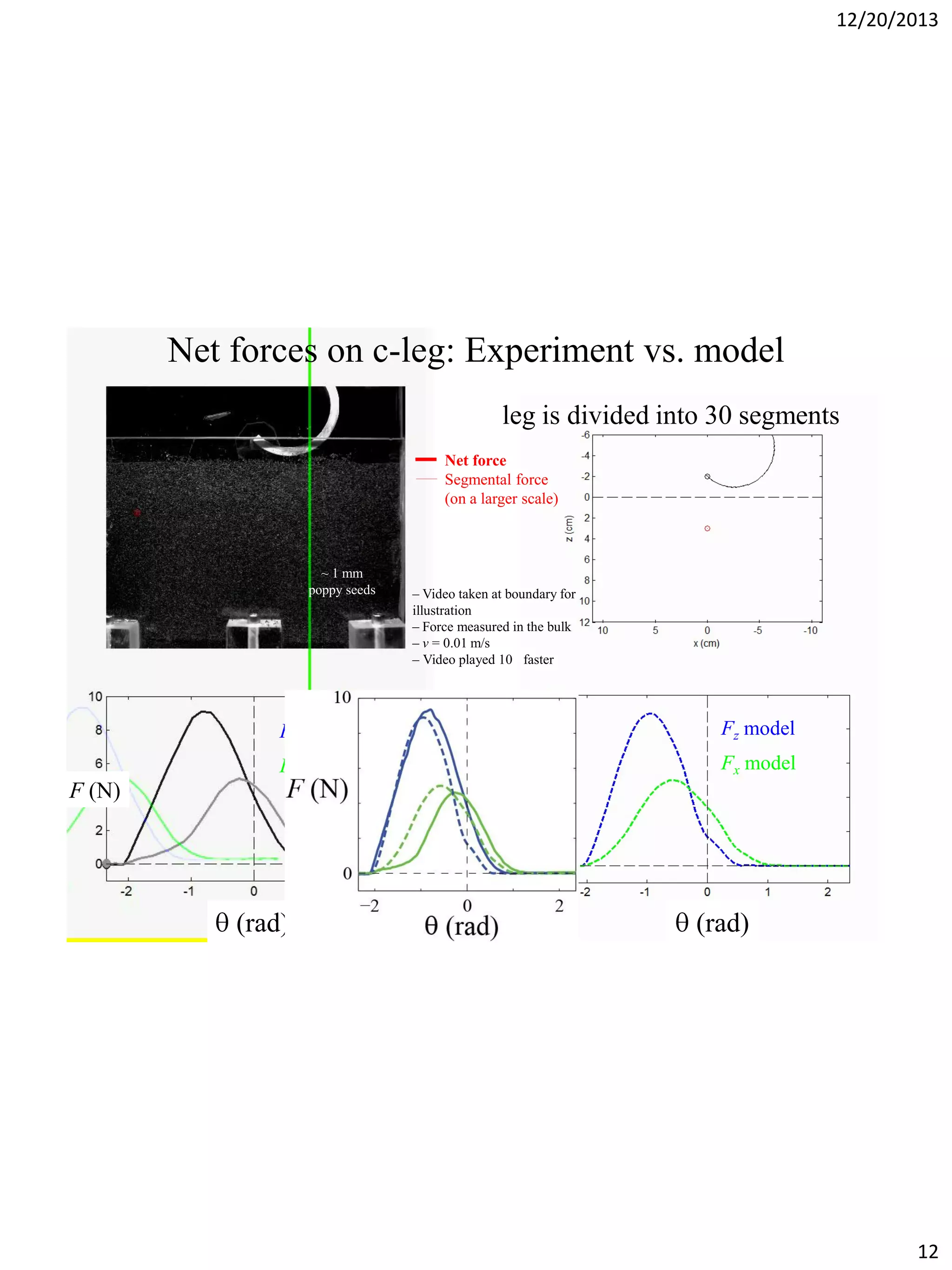
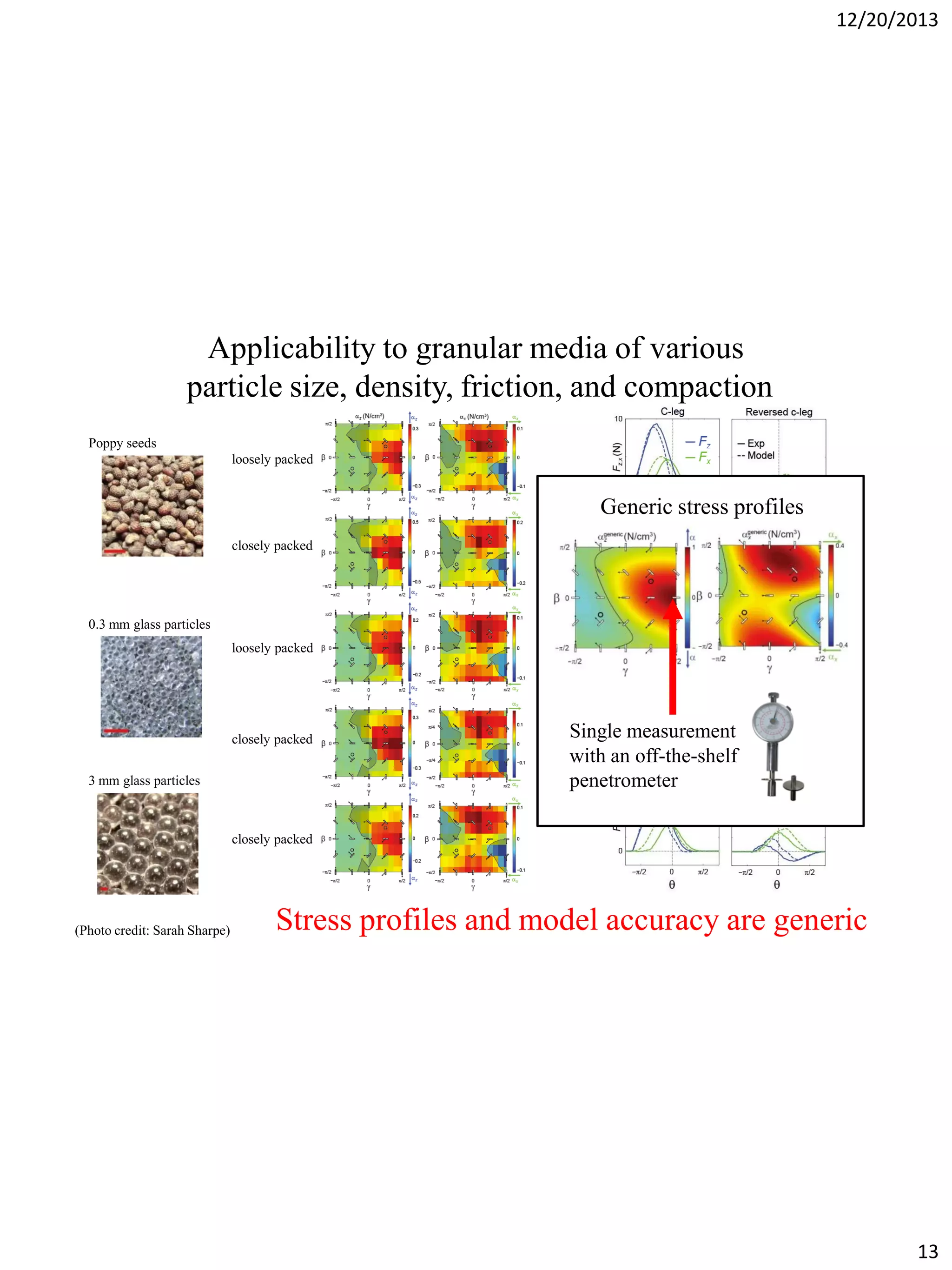
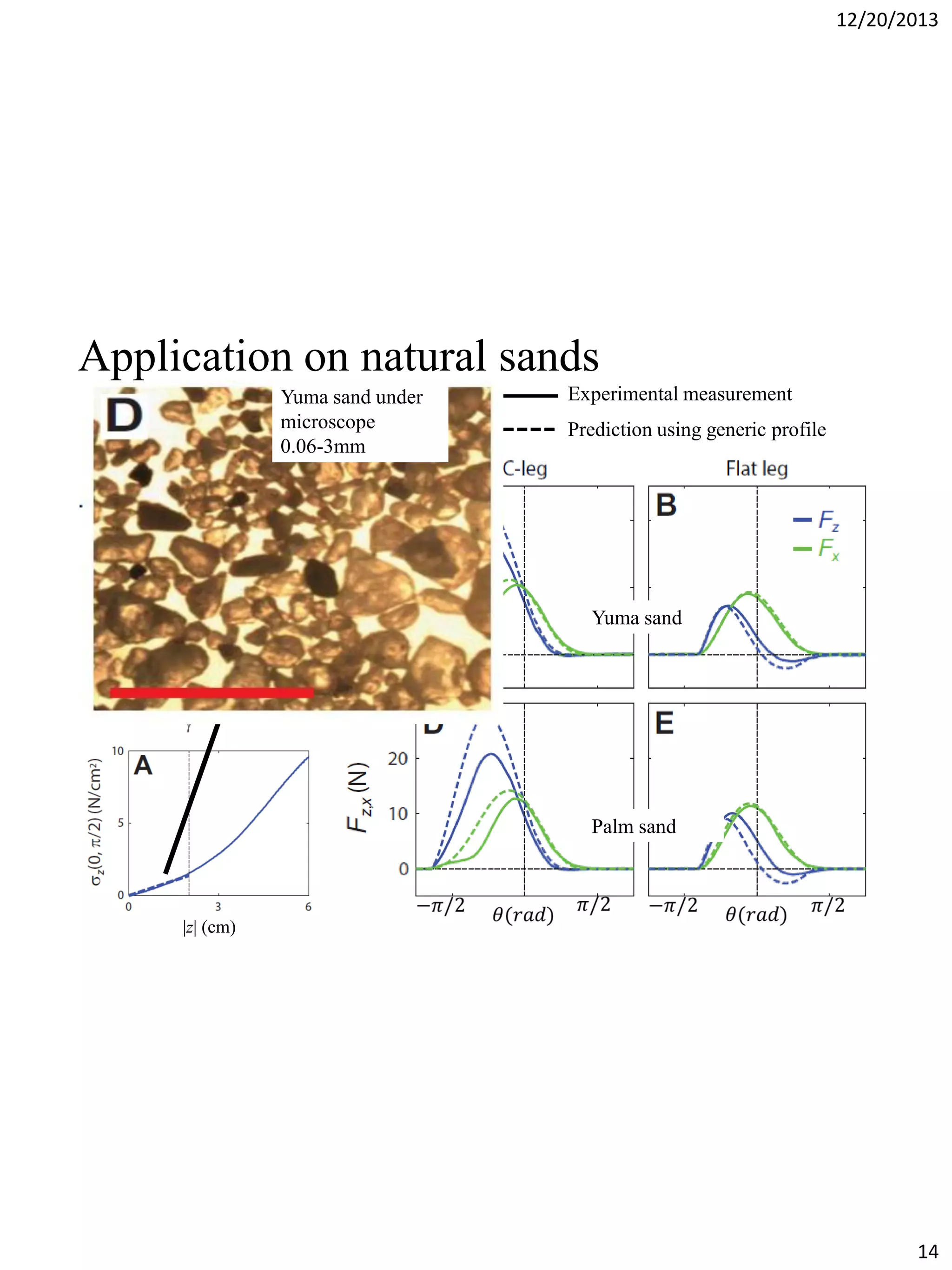
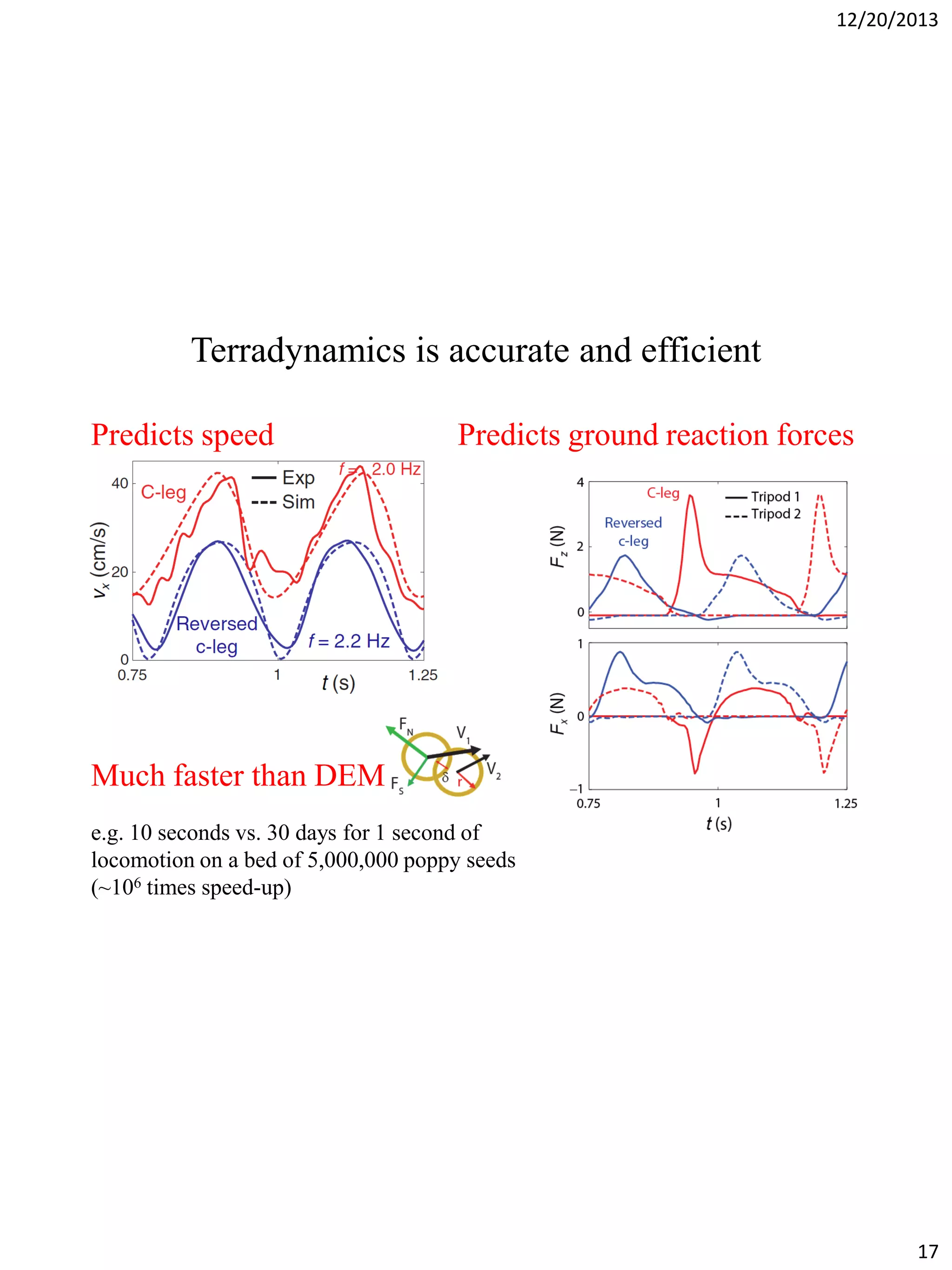
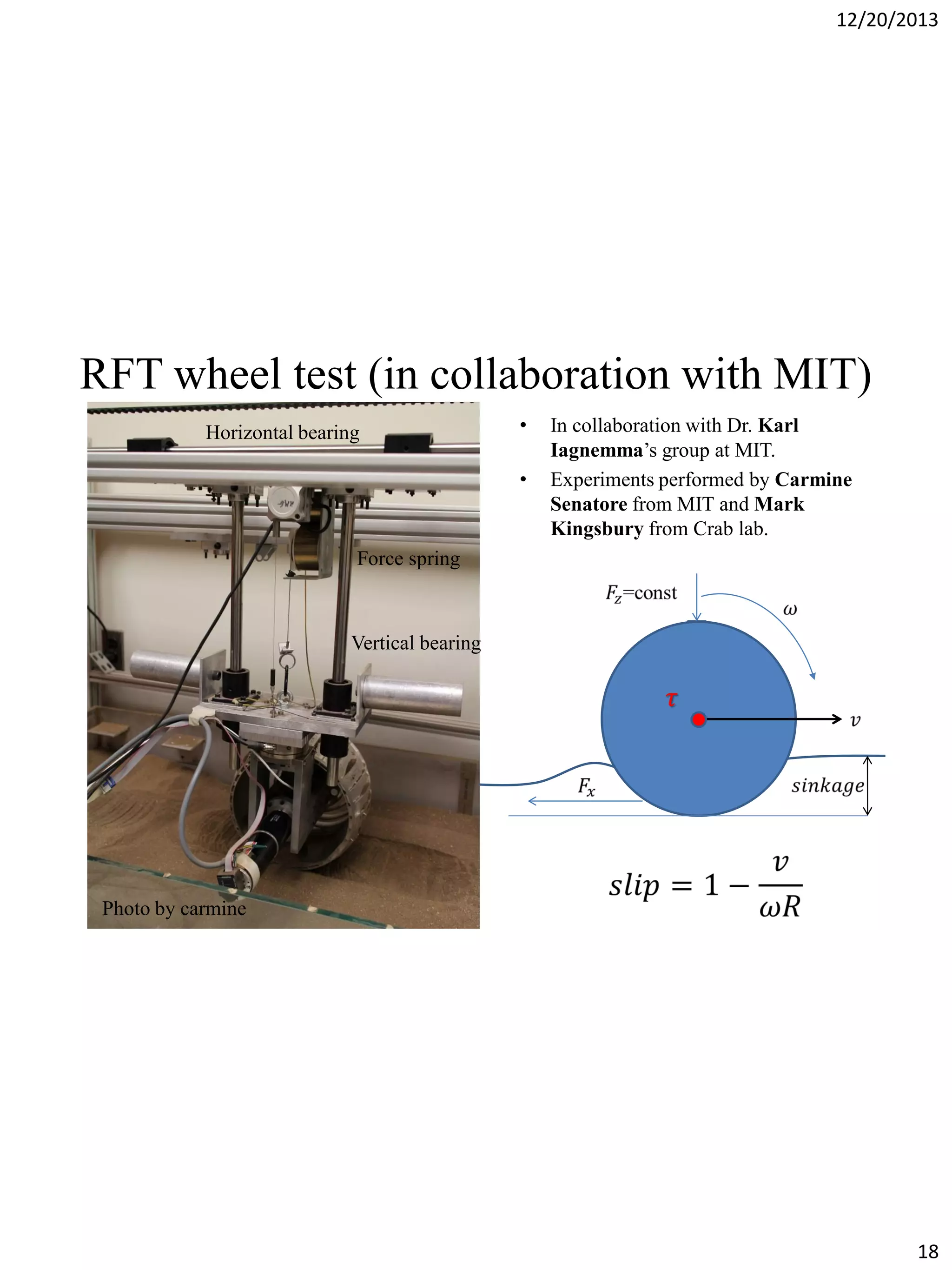
The document discusses terradynamics for legged locomotion on granular media, addressing the challenges posed by granular substrates and the complexity of limb-ground interactions. It presents a resistive force model that predicts locomotion performance without fitting parameters and compares various simulation methods, including discrete element methods and multi-body dynamics. The findings suggest that the resistive force model is effective and much faster than traditional methods for predicting performance in granular environments.

1. 12/20/2013
A Terradynamics for Legged Locomotion
on Granular Media
Tingnan Zhang*, Chen Li*†, and Daniel I. Goldman*
*School of Physics, Georgia Institute of Technology
†University of California at Berkeley
Li, Zhang, Goldman, Science (2013)
1

2. 12/20/2013
Many natural, particulate media can flow under stress
mud Martian soil
JPL
sand debris
2

3. 12/20/2013
Flowing substrates are challenging to move on
JPL
Car on sand
Tank on soil
Rover on Martian soil
Difficult to gain purchase without slipping for wheeled and
tracked vehicles alike
Kumagai (2004), IEEE Spectrum
RHex on dirt/mud
Kod*lab
Lizard vs. snake by BBC
Ghost crab
Slowed 50
3

4. 12/20/2013
Challenges: Limb-ground interaction is complex
Zebra-tailed lizard
X-ray video, slowed 50×
5 cm
Li, Hsieh, and Goldman, J. Exp. Biol. (2012)
SandBot (RHex-class)
10 cm
Slowed 10×
Li, Umbanhowar, Komsuoglu, Koditschek,
and Goldman, PNAS (2009)
Complicated morphology + kinematics
4

5. 12/20/2013
Challenges: No comprehensive force models
In fluids, Navier-Stokes
equations + moving boundary
conditions
Vogel (1996), Life in moving fluids
Flying
Swimming
Dickinson et al. (2000), Science
Comprehensive force models are lacking for general particulate media
5

6. 12/20/2013
Is terramechanics applicable?
Classical terramechanics can accurately and
quickly predict forces and performance for
(large) wheeled and tracked vehicles
Based on penetration resistance, pressuresinkage, and shear resistance tests, not
developed for legged locomotion
penetrometer
Terramechanics for
legged locomotion
?
bevameter
M. G. Bekker (1960), Off-the-road locomotion, research and
development in terramechanics
J. Y. Wong (2010), Terramechanics and off-road vehicle engineering
6

7. 12/20/2013
Discrete Element Method
dynaRoACH (10 cm, 20 g) on 3 mm glass particles
elasticity dissipation
multi-body dynamic simulation coupled to DEM
friction
Maladen, Ding, Umbanhowar, Kamor, and
Goldman, J. Roy. Soc. Interface (2011)
Zhang, Qian, Li, Masarati, Hoover, Birkmeyer, Pullin, Fearing, and Goldman, Intl. J. Robotic. Res. (2013)
Pros: Accurate
(One simulation could take a few days)
Cons: Slow, impractical for large scales
7

8. 12/20/2013
Continuum model approach?
Hypothesis: Linear superposition of independent
element forces predicts net forces
Vertical plane
• Inspired by resistive force theory for low Re number swimmers
• Valid in non-inertial regime (negligible particle inertia)
• Works for sand-swimming in horizontal plane
Lauga & Powers, Rev. Prog. Phys. (2009)
Maladen, Ding, Li, Goldman, Science (2009)
8

9. 12/20/2013
Measuring stresses using a plate element
– Video taken at boundary for
illustration
– Force measured in the bulk
– v = 0.01 m/s
– Video played 10 faster
Total force
~ 1 mm
poppy seeds
(below surface)
Extraction
Fluidization
Fully immersed
and far from
bottom
(above surface)
Stresses are hydrostatic-like
z (cm)
9

10. 12/20/2013
Stresses per unit depth vs. orientation, movement
direction
Vertical
Horizontal
Black curves:
z,x
=0
Complex dependence
10

11. 12/20/2013
Net forces on c-leg: Experiment vs. model
leg is divided into 30 segments
Net force
Segmental force
(on a larger scale)
~ 1 mm
poppy seeds
– Video taken at boundary for
illustration
– Force measured in the bulk
– v = 0.01 m/s
– Video played 10 faster
Fz experiment
Fz model
Fx experiment
Fx model
(rad)
(rad)
11

12. 12/20/2013
Net forces on c-leg: Experiment vs. model
leg is divided into 30 segments
Net force
Segmental force
(on a larger scale)
~ 1 mm
poppy seeds
– Video taken at boundary for
illustration
– Force measured in the bulk
– v = 0.01 m/s
– Video played 10 faster
Fz model
Fz experiment
F (N)
Fx experiment
(rad)
F (N)
Fx model
(rad)
12

13. 12/20/2013
Applicability to granular media of various
particle size, density, friction, and compaction
Poppy seeds
loosely packed
Generic stress profiles
closely packed
0.3 mm glass particles
loosely packed
closely packed
3 mm glass particles
Single measurement
with an off-the-shelf
penetrometer
closely packed
(Photo credit: Sarah Sharpe)
Stress profiles and model accuracy are generic
13

14. 12/20/2013
Application on natural sands
Yuma sand under
microscope
0.06-3mm
Experimental measurement
Prediction using generic profile
Yuma sand
Palm sand
z (cm)
14

15. 12/20/2013
Using resistive force model to predict legged locomotion
Xplorer (150g)
– Legs of similar friction to plate element
– Leg speeds < 0.6 m/s (non-inertial regime)
– Motion mostly confined in the vertical plane
10 cm
– Each body plate and leg is divided into
30 elements
– Total force F and torque are
calculated using resistive force model
– Body movement is calculated by:
Multibody dynamic simulator (MBDyn)
Ghiringhelli et al., Nonlinear Dynamics (1999)
15

16. 12/20/2013
Robot moving on granular media using c-legs
f = 2.0 Hz, slowed 5
c-leg
Experiment
Simulation
16

17. 12/20/2013
Terradynamics is accurate and efficient
Predicts speed
Predicts ground reaction forces
Much faster than DEM
e.g. 10 seconds vs. 30 days for 1 second of
locomotion on a bed of 5,000,000 poppy seeds
(~106 times speed-up)
17

18. 12/20/2013
RFT wheel test (in collaboration with MIT)
Horizontal bearing
•
•
In collaboration with Dr. Karl
Iagnemma’s group at MIT.
Experiments performed by Carmine
Senatore from MIT and Mark
Kingsbury from Crab lab.
Force spring
Vertical bearing
Photo by carmine
18

19. 12/20/2013
MER wheel on fluidized bed
19

20. 12/20/2013
Wheels and testing conditions
McMaster
Small
McMaster
Large
3D Printed
MIT Smooth
Diameter [mm]
152.4
203.2
145 (to lug tips)
260
Width [mm]
44.5
50.8
76.2
160
Fz Tested [N]
7
20
10, 18
60, 120
Loose
Loose and
Compact
Loose and compact
(only for 18 N)
Loose and
Compact
Terrain State Tested
(Poppy seeds)
McMaster
Small
McMaster
Large
3D Printed
MIT Smooth (approx. to scale)
20

21. 12/20/2013
Drawbar vs. slip ratio in experiment and model
Experiment
WR
RFT
10
Drawbar [N]
5
0
-5
-0.5
0
0.5
Slip
21

22. 12/20/2013
Experiment
WR
RFT
10
3D Printed
Fz = 18 N
Compact
Drawbar [N]
5
0
-5
-0.5
0
0.5
Slip
0.8
25
Sinkage [mm]
Torque [Nm]
0.6
0.4
0.2
15
10
0
-0.2
20
-0.6 -0.4 -0.2
0
Slip
0.2
0.4
0.6
-0.6 -0.4 -0.2
0
0.2
0.4
0.6
Slip
22

23. 12/20/2013
Experiment
WR
RFT
6
4
McMaster
Large
Fz = 20 N
Compact
Drawbar [N]
2
0
-2
-4
-6
-8
-10
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
Slip
35
1
30
Sinkage [mm]
Torque [Nm]
0.8
0.6
0.4
0.2
25
20
15
0
10
-0.2
-0.6 -0.4 -0.2
0
Slip
0.2
0.4
0.6
5
-0.6 -0.4 -0.2
0
0.2
0.4
0.6
Slip
23

24. 12/20/2013
Summary
1. Developed a resistive force model in the vertical plane for legged
locomotion on granular media (for slow intrusions)
2. Resistive force model predicts forces (without any fitting
parameters) on intruders of complex morphology and kinematics
3. Resistive force model + multi-body simulation predicts legged robot
performance
4. RFT is able to predict wheel performance under a wide range of
conditions.
24

25. 12/20/2013
Acknowledgements:
Yang Ding, Nick Gravish, Paul Umbanhowar, Gareth Meirion-Griffith, and Hal Komsuoglu for
discussion. Jeff Shen for robot modification. Pierangelo Masarati for MBDyn support. Sarah
Sharpe for taking the photos of granular materials. Paul Umbanhowar and Hamid Marvi for
assistance with natural sand collection.
Funded by: Burrough’s Wellcome Fund, ARL MAST CTA, ARO, NSF PoLS and Miller Research
Fellowship (C.L.).
25

26. 12/20/2013
Starting point: level, uniform, dry granular media
1 cm
Granular media (e.g., sand and gravel):
collections of discrete particles that interact
through dissipative, repulsive contact forces
Nedderman (1992), Statics and Kinematics of Granular Materials
A convenient model flowing substrate for locomotion studies:
representative, relevant, relatively simple, controllable
~ 1 mm
poppy seeds
A fluidized bed
prepares repeatable
packing states
Air flow
Jackson (2000),
The Dynamics of
Fluidized Particles
Air flow
26

27. 12/20/2013
3
McMaster
Small
Fz = 7 N
Loose
Experiment
WR
RFT
2
Drawbar [N]
1
0
-1
-2
-3
-4
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
Slip
0.3
30
0.25
25
Sinkage [mm]
Torque [Nm]
0.2
0.15
0.1
0.05
0
20
15
10
-0.05
-0.5
0
Slip
0.5
-0.6 -0.4 -0.2
0
0.2
0.4
0.6
Slip
27

28. 12/20/2013
Drawbar [N]
5
Experiment
WR
RFT
McMaster
Large
Fz = 20 N
Loose
0
-5
-10
-0.6 -0.4 -0.2
0
0.2
0.4
0.6
Slip
1.2
50
1
Sinkage [mm]
Torque [Nm]
0.8
0.6
0.4
0.2
40
30
20
0
10
-0.2
-0.6 -0.4 -0.2
0
Slip
0.2
0.4
0.6
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
Slip
28

29. 12/20/2013
Experiment
WR
RFT
6
4
McMaster
Large
Fz = 20 N
Compact
Drawbar [N]
2
0
-2
-4
-6
-8
-10
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
Slip
35
1
30
Sinkage [mm]
Torque [Nm]
0.8
0.6
0.4
0.2
25
20
15
0
10
-0.2
-0.6 -0.4 -0.2
0
Slip
0.2
0.4
0.6
5
-0.6 -0.4 -0.2
0
0.2
0.4
0.6
Slip
29

30. 12/20/2013
3
Experiment
WR
RFT
2
Drawbar [N]
1
3D Printed
Fz = 10 N
Loose
0
-1
-2
-3
-4
-5
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
Slip
25
0.4
Sinkage [mm]
20
Torque [Nm]
0.3
0.2
0.1
15
10
0
-0.1
-0.6 -0.4 -0.2
0
Slip
0.2
0.4
0.6
-0.5
0
0.5
Slip
30

31. 12/20/2013
Experiment
WR
RFT
Drawbar [N]
5
3D Printed
Fz = 18 N
Loose
0
-5
-10
-0.6 -0.4 -0.2
0
0.2
0.4
0.6
Slip
35
30
Sinkage [mm]
Torque [Nm]
0.6
0.4
0.2
25
20
15
0
10
-0.2
-0.6 -0.4 -0.2
0
Slip
0.2
0.4
0.6
-0.5
0
0.5
Slip
31

32. 12/20/2013
Experiment
WR
RFT
10
3D Printed
Fz = 18 N
Compact
Drawbar [N]
5
0
-5
-0.5
0
0.5
Slip
0.8
25
Sinkage [mm]
Torque [Nm]
0.6
0.4
0.2
15
10
0
-0.2
20
-0.6 -0.4 -0.2
0
Slip
0.2
0.4
0.6
-0.6 -0.4 -0.2
0
0.2
0.4
0.6
Slip
32

33. 12/20/2013
30
Experiment L
Experiment C
WR L
WR C
RFT L
RFT C
Drawbar [N]
20
10
0
MIT Wheel
Fz = 60 N
Compact/Loose
-10
-20
-30
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
50
Slip
4
40
Sinkage [mm]
Torque [Nm]
3
2
1
0
30
20
10
-1
-0.5
0
Slip
0.5
-0.6 -0.4 -0.2
0
0.2
0.4
0.6
Slip
33

34. 12/20/2013
Experiment L
Experiment C
WR L
WR C
RFT L
RFT C
40
Drawbar [N]
20
0
MIT Wheel
Fz = 120 N
Compact/Loose
-20
-40
-60
-0.6 -0.4 -0.2
0
0.2
0.4
8
60
50
Sinkage [mm]
6
Torque [Nm]
0.6
Slip
4
2
40
30
20
0
10
-2
-0.6 -0.4 -0.2
-0.5
0
0.5
0
0.2
0.4
0.6
Slip
Slip
34