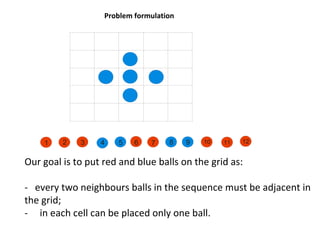
This document proposes a new integer programming model for the HP protein folding problem. [1] It formulates the HP lattice model as a graph problem to maximize the number of contacts between hydrophobic (H) amino acids. [2] The model defines binary variables to represent amino acid placement and contact edges between nodes in the lattice. [3] Computational experiments apply the model to fold two protein sequences on a 3D cubic lattice and present the results graphically.

1. A new integer programming model for HP problem
N. Yanev 1, P. Milanov 2; 3, I. Trenchev 2
1 Faculty of Mathematics and Informatics, University of Sofia, Bulgaria.
2 South-West University “Neot Rilski", Blagoevgrad, Bulgaria.
3 Institute of Mathematics and Informatics, Bulgarian Academy of Sciences.
choby@math.bas.bg, peter milanov77@yahoo.com, trenchev@swu.bg

2. Problem formulation
1 2 3 4 5 6 7 8 9 10 11 12
Our goal is to put red and blue balls on the grid as:
- every two neighbours balls in the sequence must be adjacent in
the grid;
- in each cell can be placed only one ball.

3. Problem formulation
A self-avoiding walk is a path from one point
to another which never intersects itself.
Such paths are usually considered to occur
on lattices, so that steps are only allowed in
a discrete number of directions and of
certain lengths.

4. Goal: problem maximizes the number
of blue, blue pairs of contacts

6. From Protein folding to HP model
Amino acids sequence: HP folding sequence :
SLDRSSCFTGSLDSIRAQSGLGCNSFRY PHPPPPPHPPPHPPHPHPPPHPPPPHPP
In this research, we study the hydrophobic-hydrophilic (HP) model on two-dimensional
(2D) square lattice, which is one of the most extensively studied lattice models. The HP
model was first introduced by Dill (1985).

7. Optimal vs heuristics
Figure 3: Optimal fold of a protein of length Figure 2: A fold constructed by the Hart-
36 Istrail algorithm

8. Conversion to Graph problem
16
15
14
13
12
11
10
x 9
8
7
x
6
x 5
1 2 3 4 4
3
2
1
H H P P H P

9. Mathematical problem is to find a path in the graph from first
column to the last with maximum green arcs

10. Let L(i, k) be integer lattice . Let for 2D or 3D lattices: N = n 2 or N = n 3 .
For any vertex i, k L (in column i ϵ L and row k ϵ L), are defined binary variables xi,k and
zi,j,k,l such that:
1 if the k th amino - acid is in the cell i

xi ,k = 
0 otherwise,
 .
where i = 1..N k = 1..n.
1 if the edge (i, k, j, l) is contact between two HH amono acids,
z i , k , j ,l = 
 0 otherwise, .
where i, j = 1..N, k, l = 1..n.
Let the set G(i) denotes all possible neighborhood of i. The number of elements of
G(i) for 2D lattices is 4 and for 3D lattices is 6.

11. The optimal solution of the linear problem is bounded
by the following upper bound:
2.min{E, O}+k,
where
k = 0, if no H amino acids are placed in the first and
last positions,
1, if a H amino acid is placed in the first or last
position,
2, if two H amino acids are placed in the first and
last positions
E and O represent the sets of H amino acids in even
position and odd position of the sequence,
respectively.

12. Computational runs
We used a 3D cubic lattice with dimension 6 .
The primary sequence of these two proteins is:
SLDRSSCFTGSLDSIRAQSGLGCNSFRY – orexin peptide;
FSGPPGLQGRLQRLLQASGNHAAGILTM – hypotensive hormone.
Figure 4. Graphical presentation for HP folding of 1ANP

13. Future trends:
• Improving of the model;
• Adaptation of CPLEX for special branch and
bound for HP folding;
• Solving larger problems.

14. Thank you for
attention.