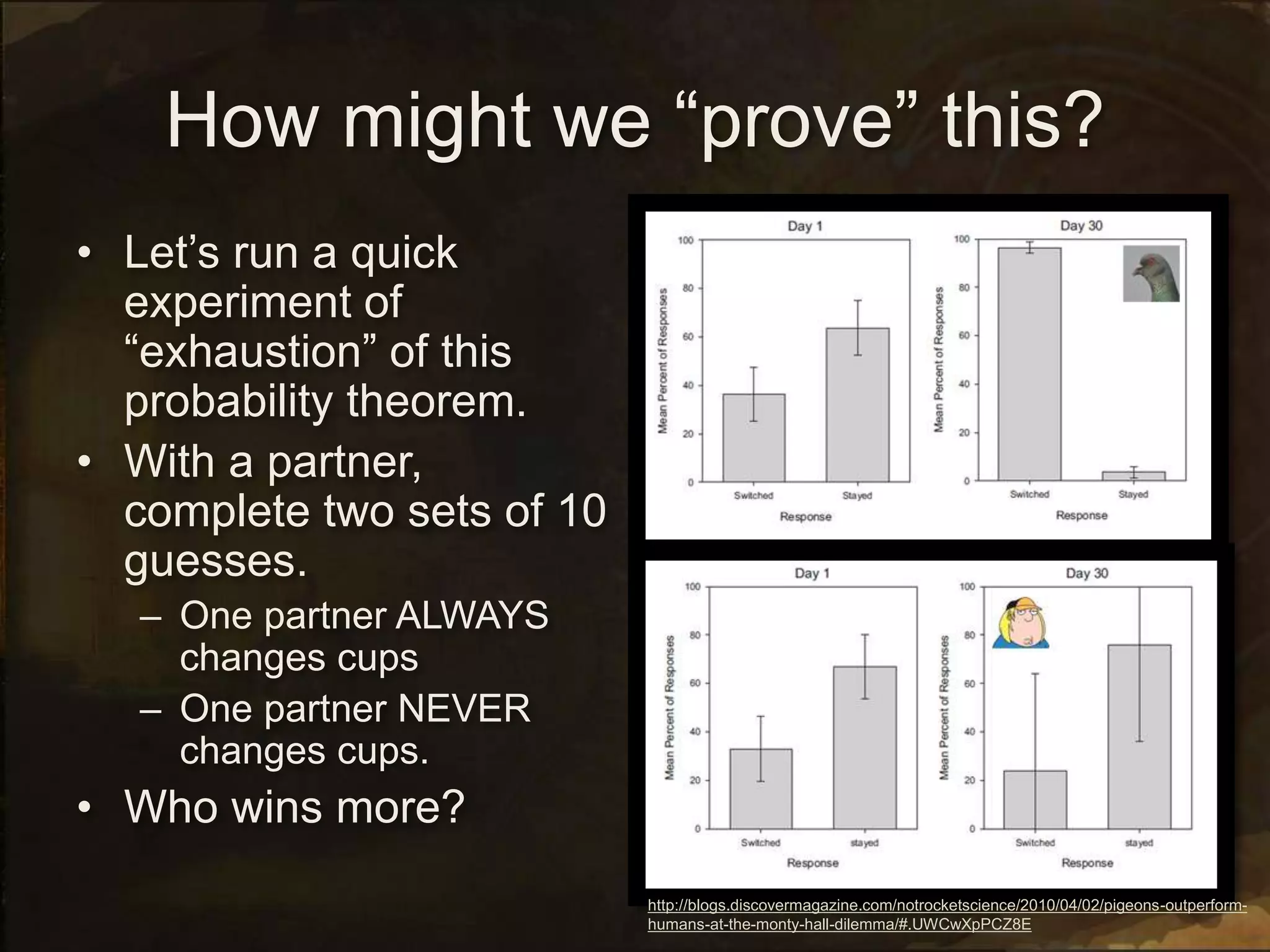
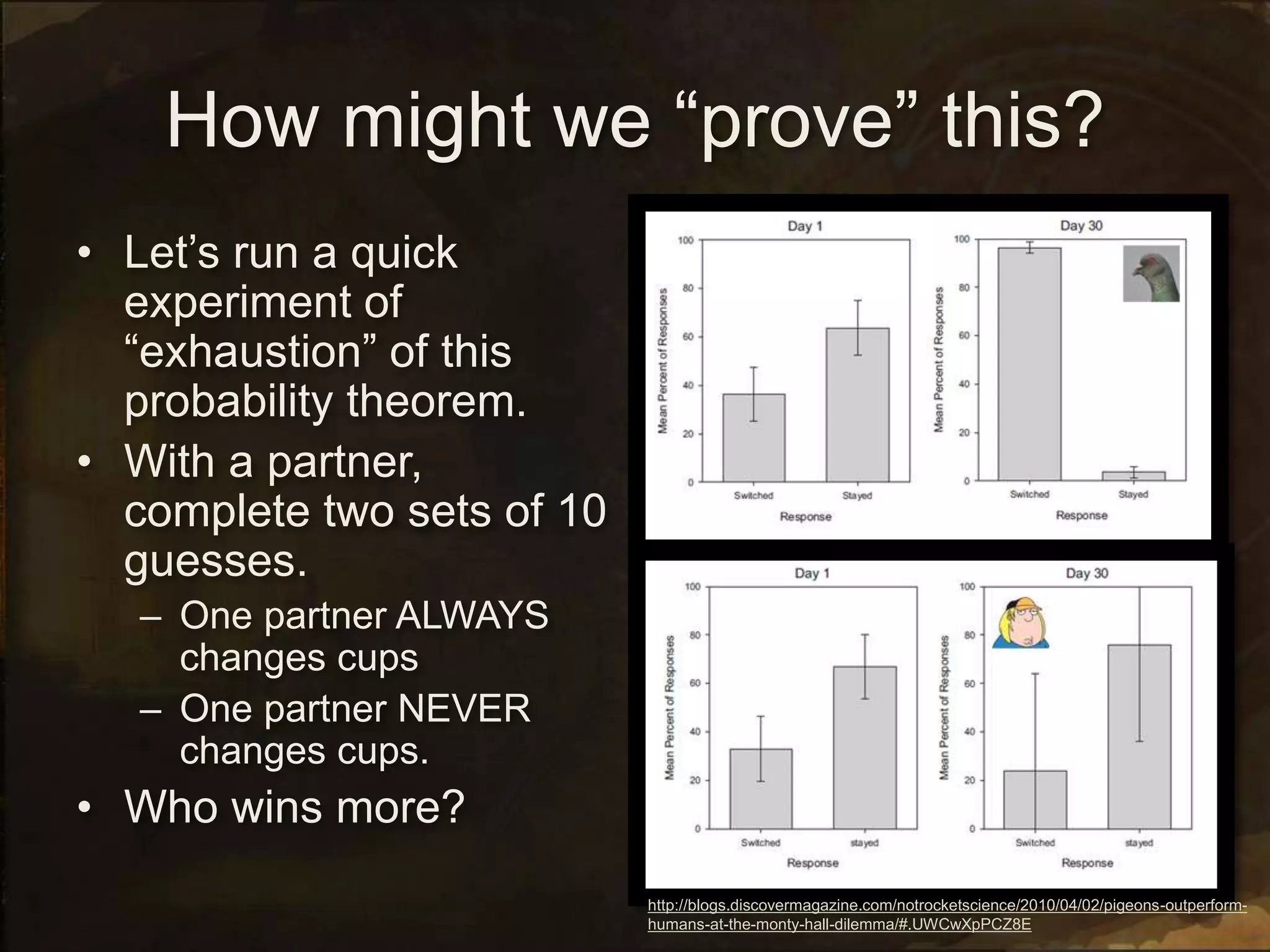
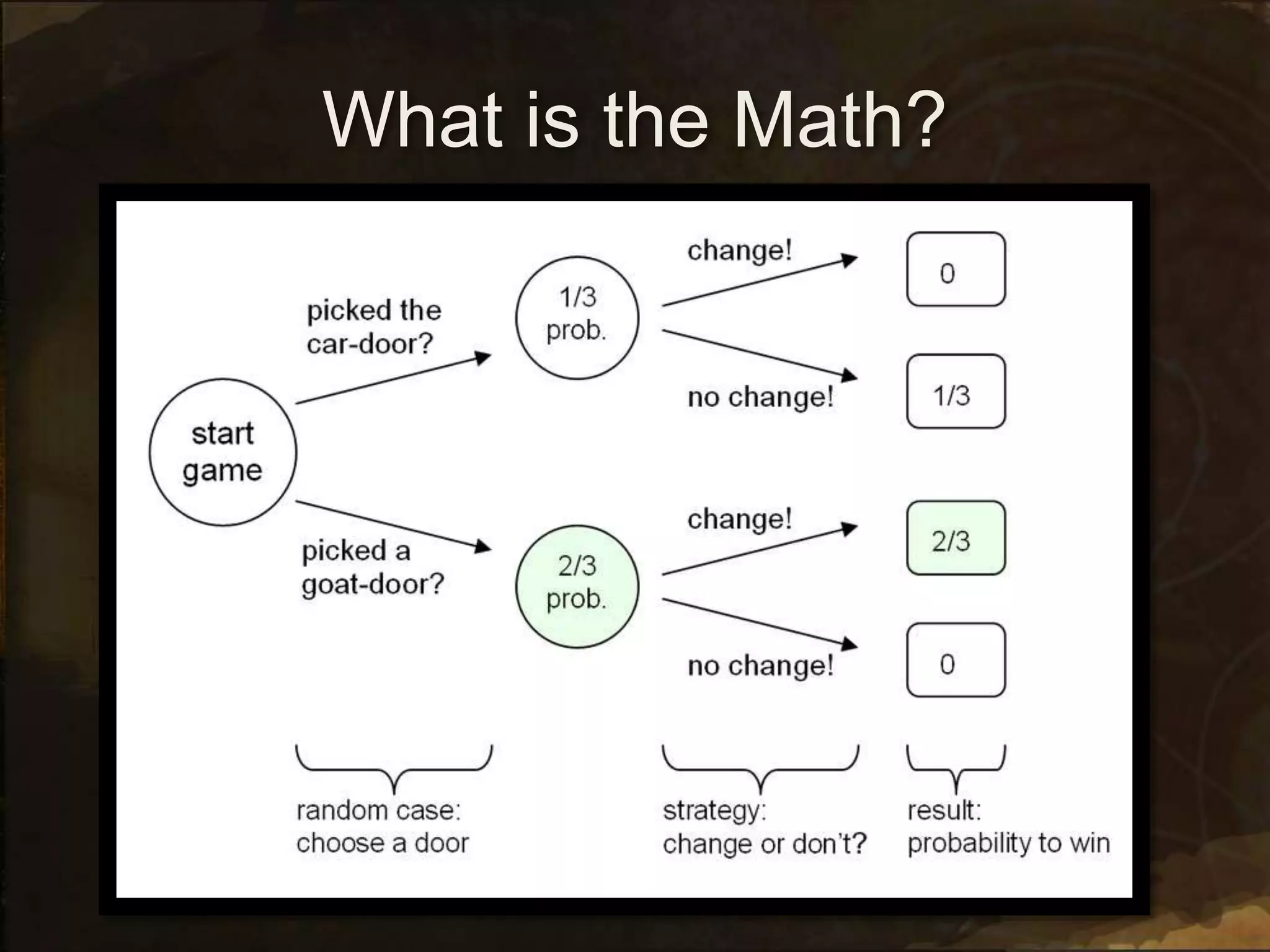
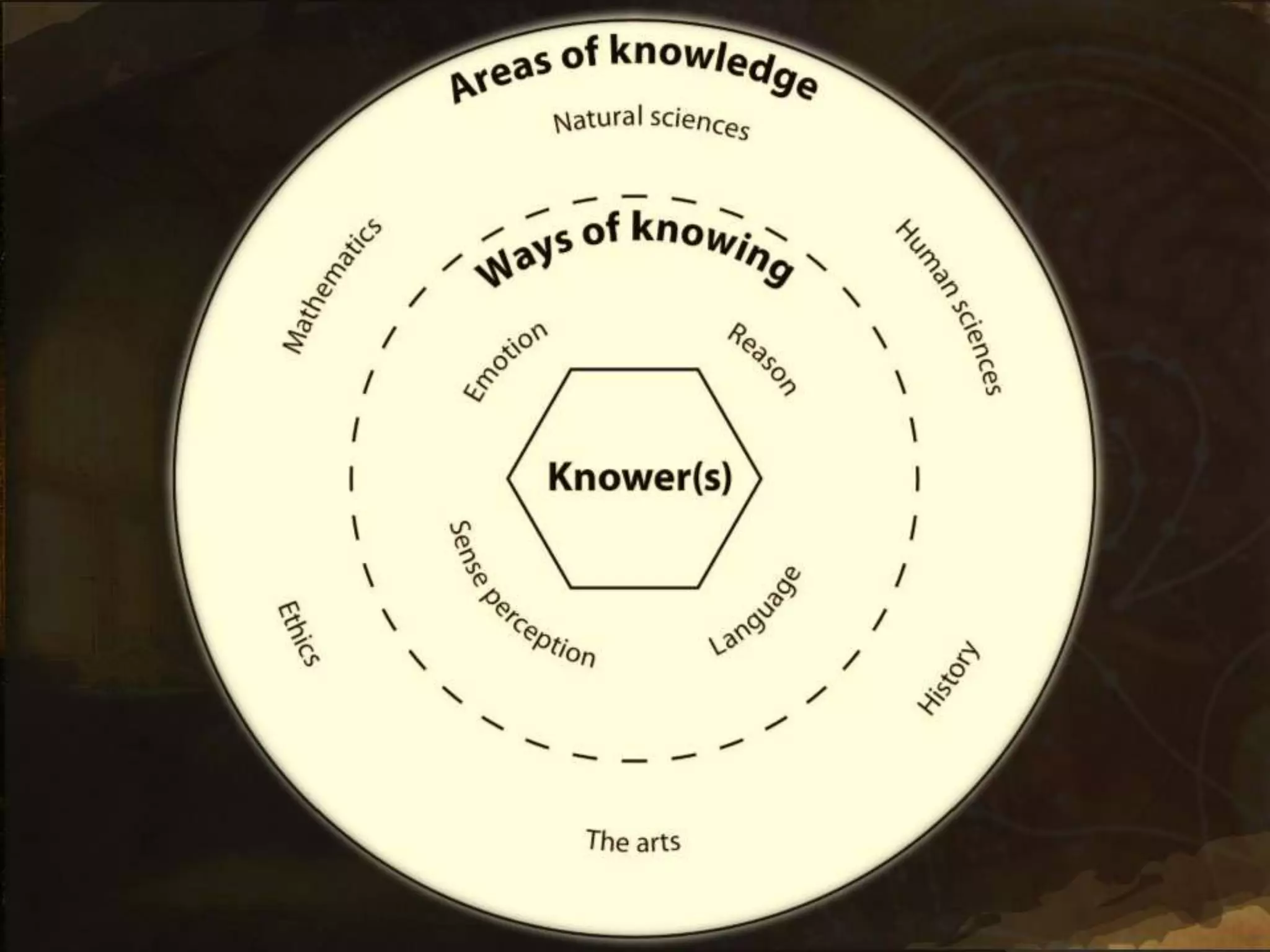
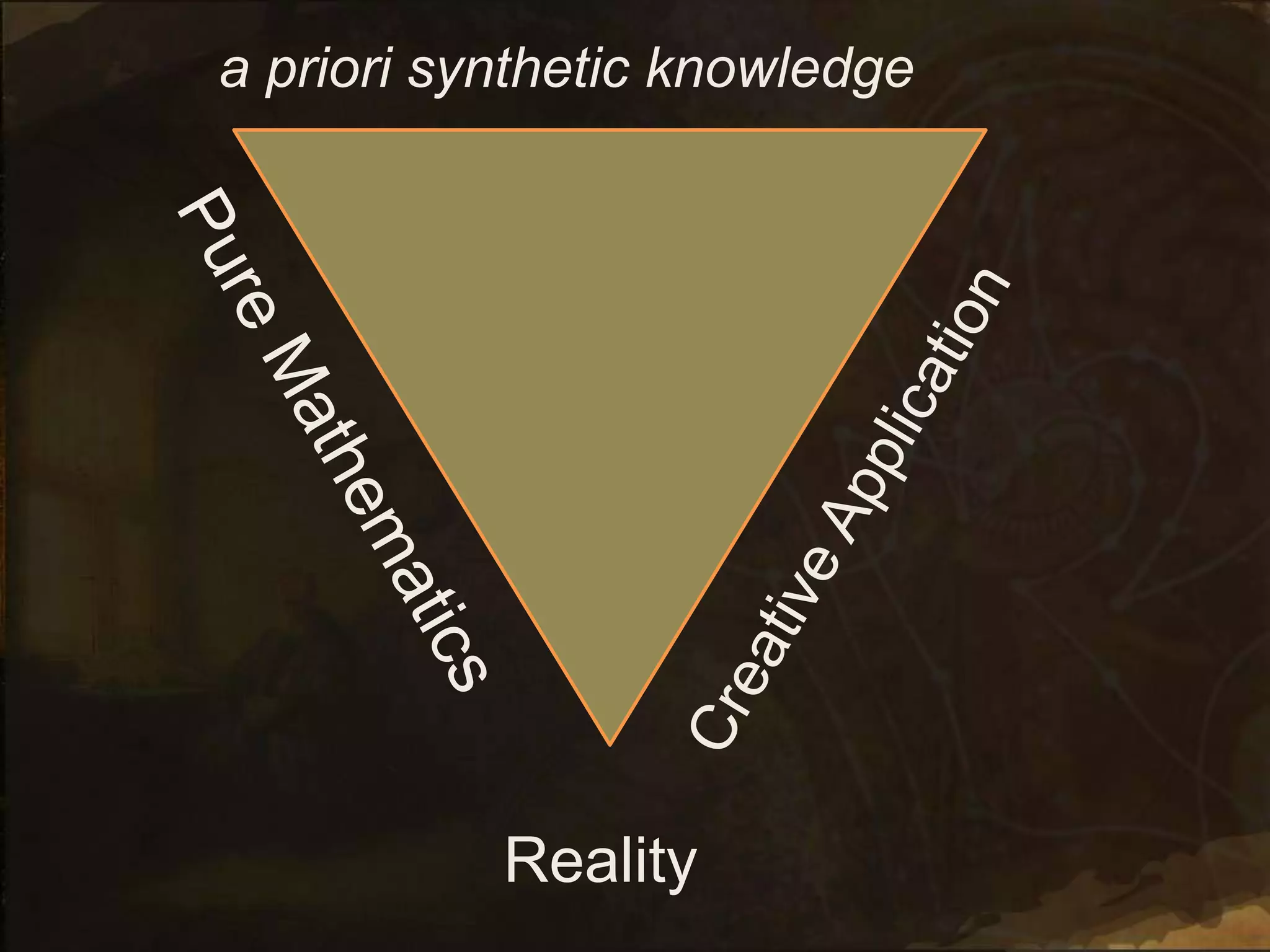
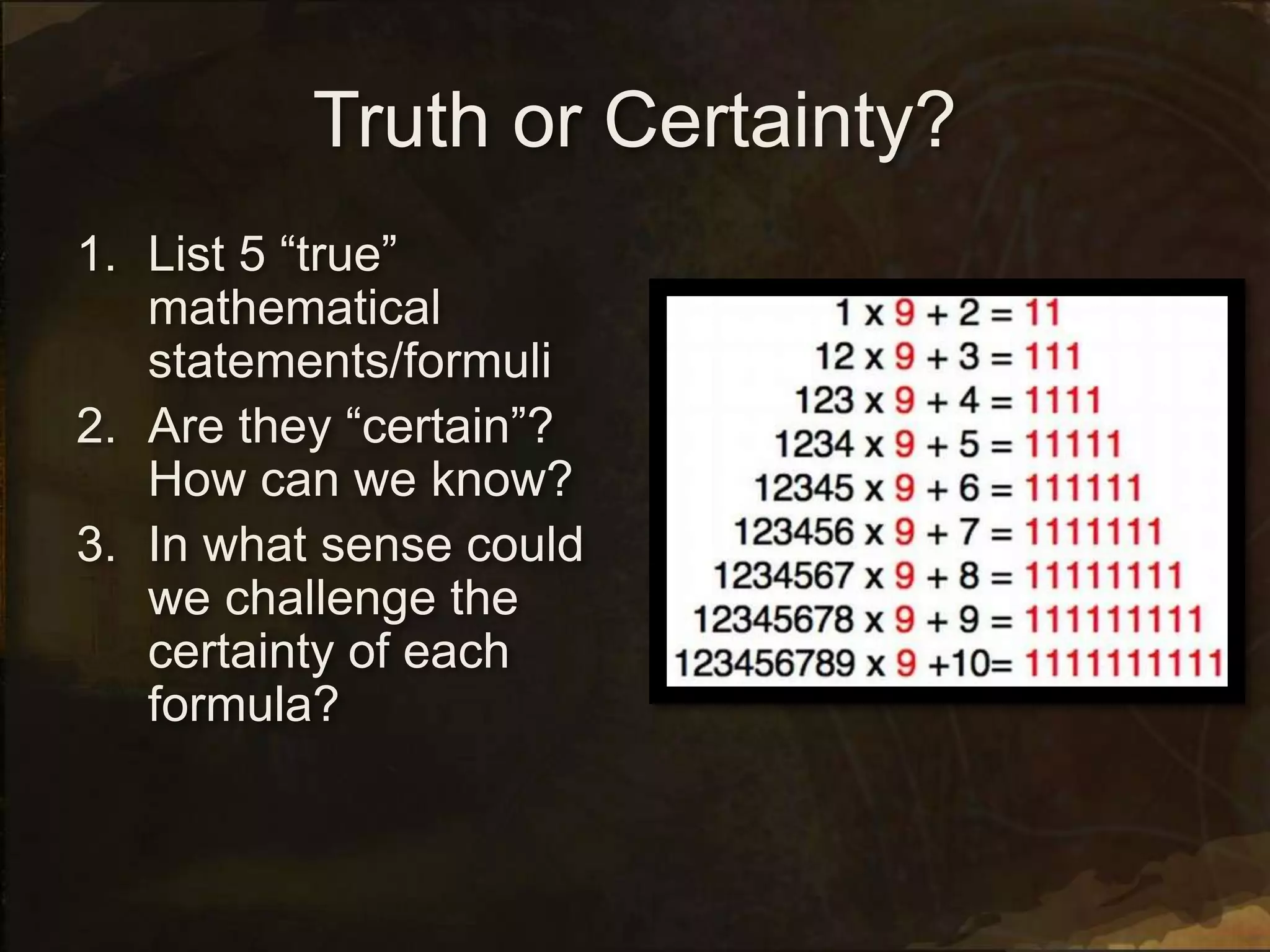
1. The document outlines the agenda for a mathematics class, including readings on history of mathematics, a podcast, and activities on mind reading, the Monty Hall problem, and coloring shapes. 2. It discusses definitions of mathematics, axioms, theorems, and the relationship between math and reality. Concepts like a priori synthetic knowledge and the certainty of mathematical statements are examined. 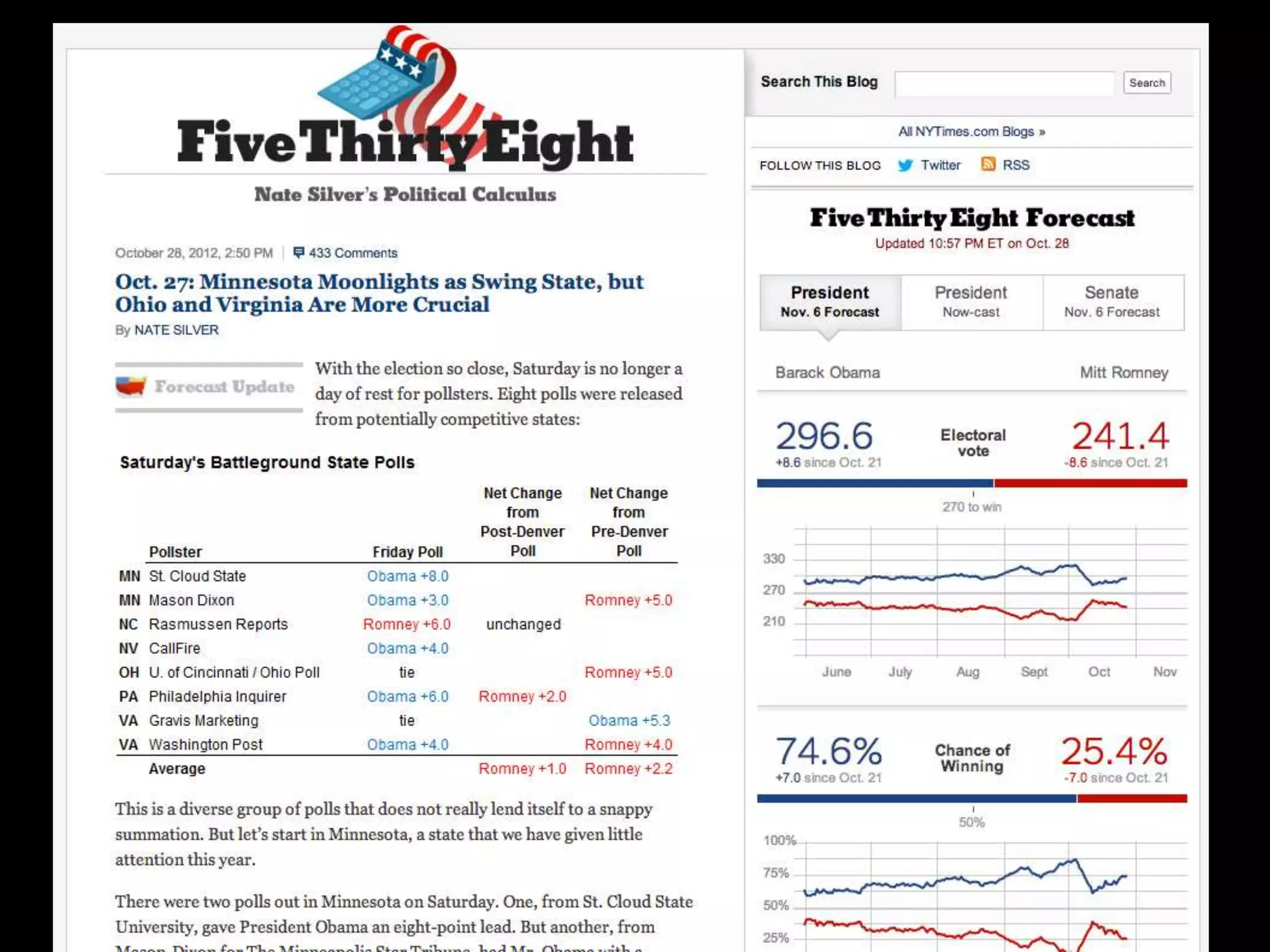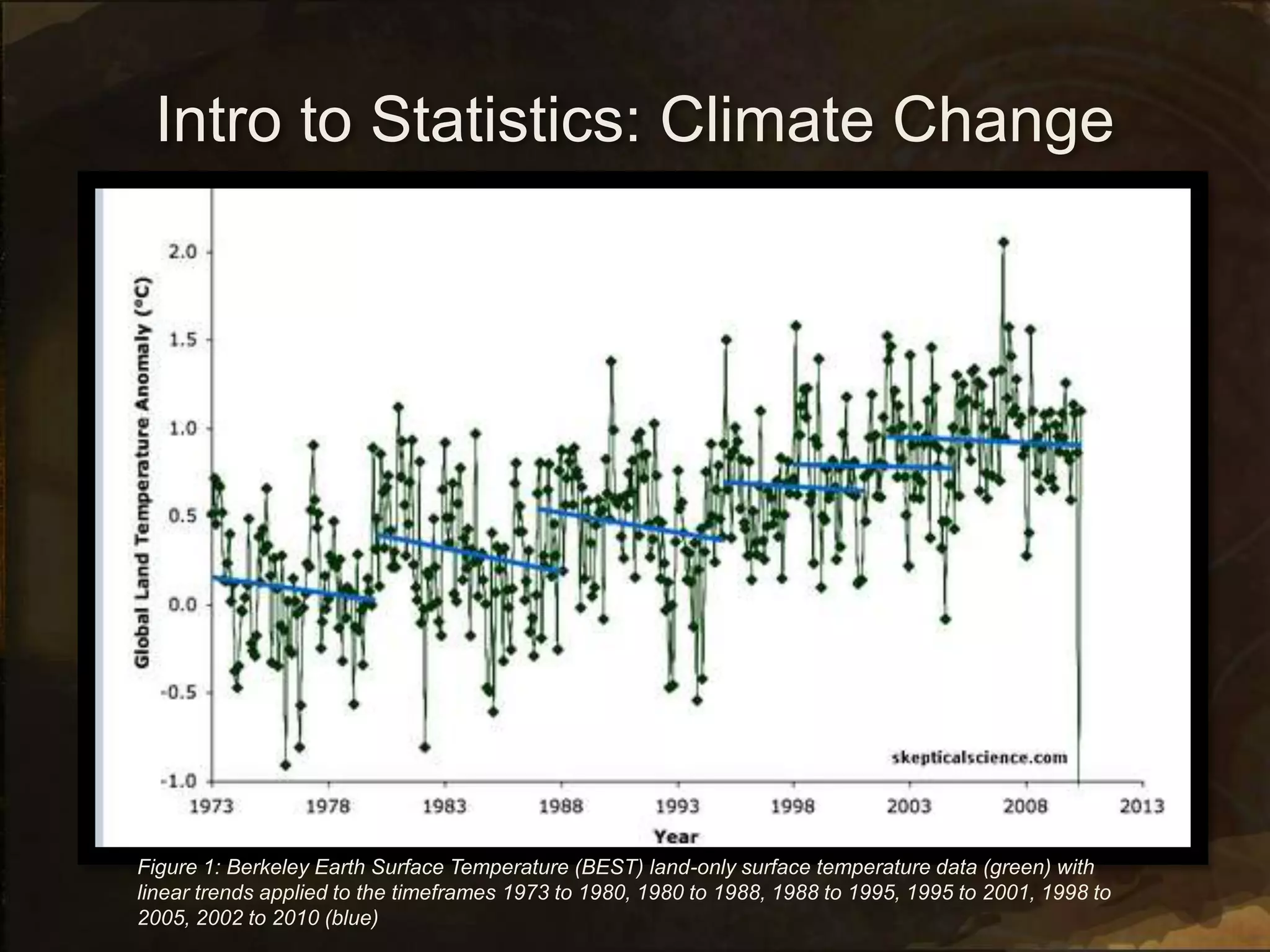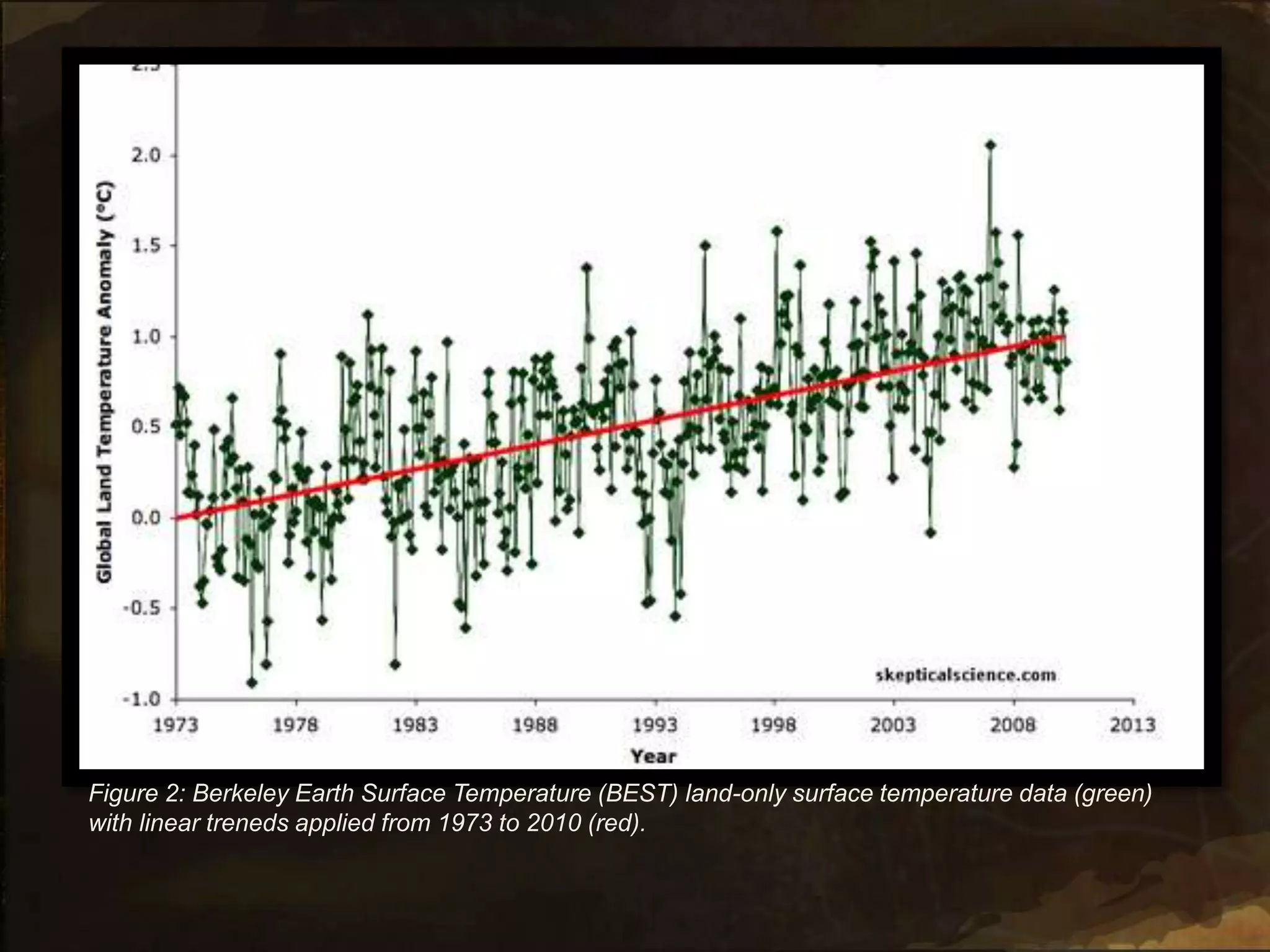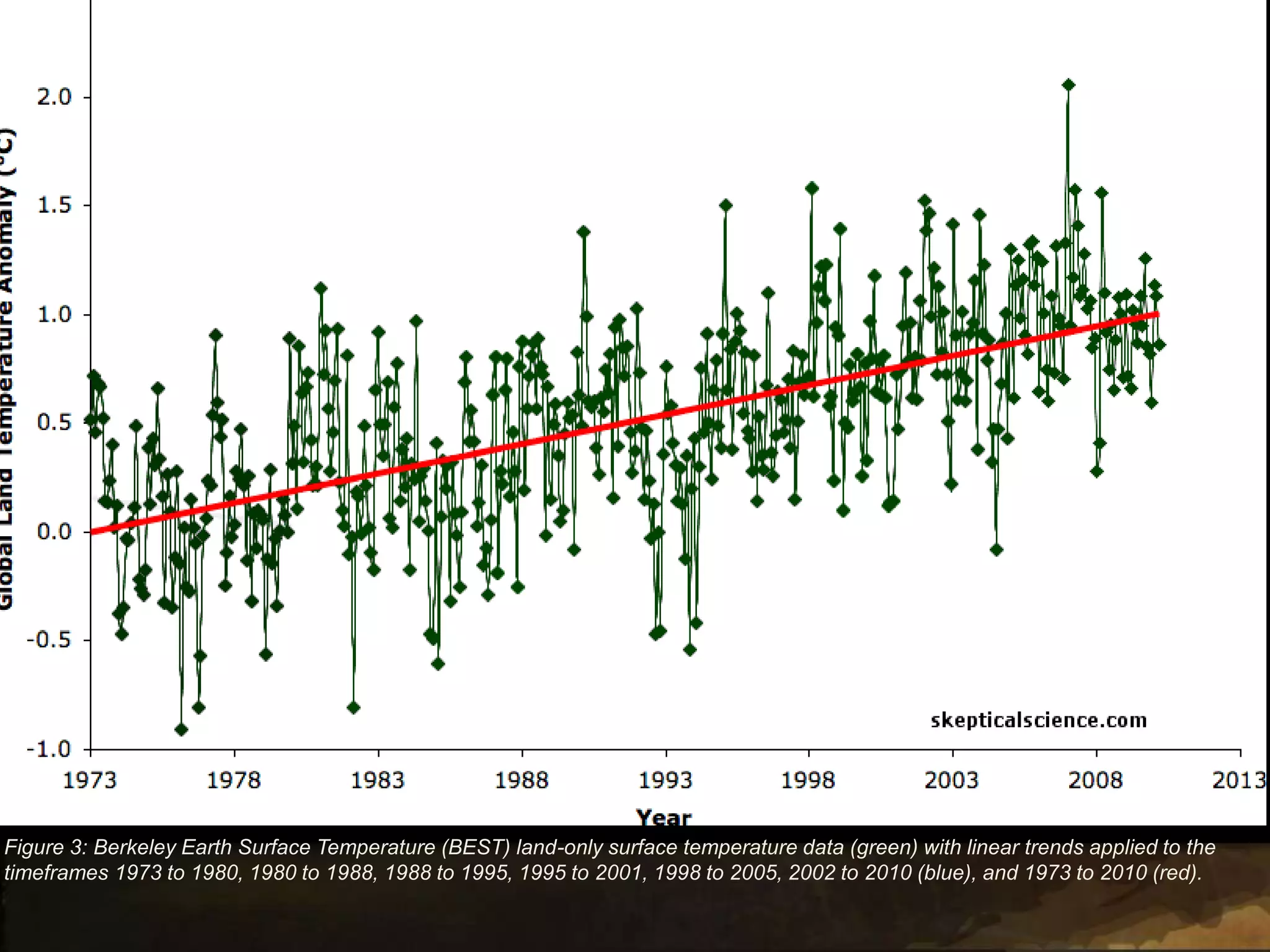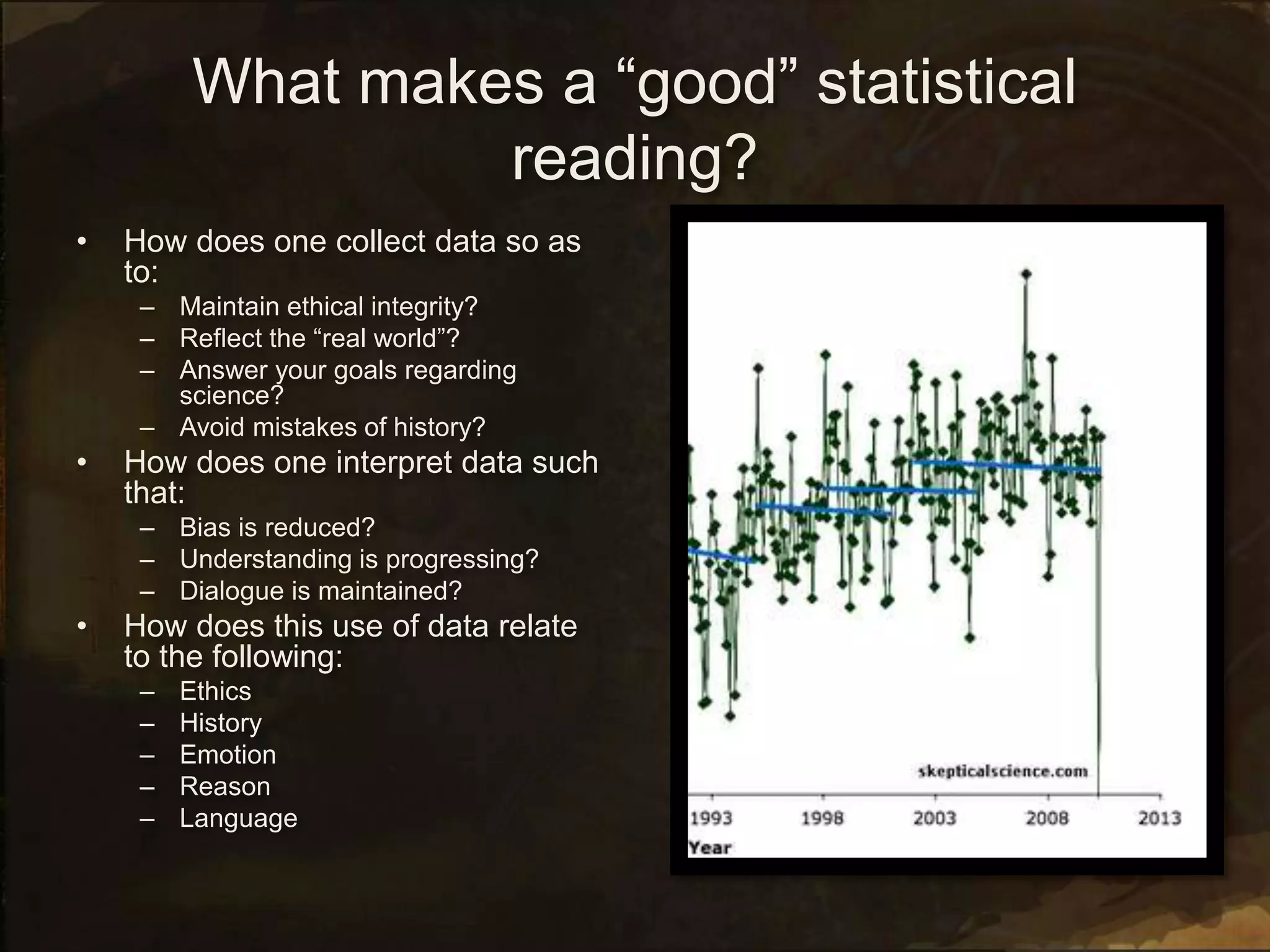3. On Wednesday, students will discuss how statistics and probability relate to their Extended Essay topics and how different interpretations of data affect understanding. They will pose questions about the mathematical aspects of their topics.

1. Mathematics Method
AIO: Climate Change
PP: Albert Einstein or Kurt Godel
Socratic Seminar: History (Thursday)
• Readings:
1. P. 133-137
2. P. 138-143
3. P. 144-147
4. P. 148-150
5. P. 151-152
6. A brief history of
Mathematics
Podcast
http://www.bbc.co.uk/podcasts/series/maths

2. Activity: Mind Reading?
• I will attempt to read 5
students’ minds with
only the most basic of
information.
• PoK question: How do
we use math to
anticipate and predict
future “knowing”? Is
math superior in this
regard to the other
areas of knowledge?

4. Where we are Going?
• Definitions and
Philosophy
• Axioms and
Theorem
• Truth vs. Certainty
• Math and Culture
• Art Connection
Let me see: four times five is twelve, and four times six is thirteen, and four times
seven is–oh dear! I shall never get to twenty at that rate!

5. Mathematics and Prediction
• Nate Silver used
computer simulations to
accurately predict every
State’s outcome during
the recent presidential
election.
• Was ridiculed by
pundits, who believed it
was “impossible” to
know who was going to
win such a close
election.

7. What is Mathematics?
1. Mathematics is founded on a set
of more or less universally
accepted definitions and basic
assumptions.
2. It proceeds from a system of
axioms using deductive
reasoning to prove theorems or
mathematical truths.
3. These theorems have a degree
of “certainty” that is unmatched
by other areas of knowing
4. Question: Should Mathematics
be an area, or a way of
knowing? How is Math different
from “Reason”?

9. Math as “Ding an Sich”
• Kant posited that Math could
provide knowledge that is more
than purely logical (a priori
synthetic knowledge).
• How can math give us
knowledge of the “thing in
itself” beyond empirical
knowing?
• Presupposes that Space and
Time our “forms for our intuition”
not a “Ding an Sich”

10. If two sides of a triangle are
congruent, the angles opposite
them are congruent.
How does this theorem give us
“synthetic knowledge” of reality?
How is it different than formal logic?

11. Reality
a priori synthetic knowledge

13. Math and Academic Rigor
1. A proof of a formula A is a
finite list of formula's in which
A is the last formula, and all
formula's are either axioms or
follow from an formula or
formula's earlier mentioned in
the list by an rule of inference.
2. Direct proof, induction,
transposition (logic),
contradiction, construction,
exhaustion, probablistic, etc.
3. Consider the visual proof of
the Pythagorean Theorem,
how is this a proof? What
does this tell us about reality?

14. Truth or Certainty?
1. List 5 “true”
mathematical
statements/formuli
2. Are they “certain”?
How can we know?
3. In what sense could
we challenge the
certainty of each
formula?

15. 1=0 “Proof”?
x = y.
Then x2 = xy.
Subtract the same thing from both sides:
x2 - y2 = xy - y2.
Dividing by (x-y), obtain
x + y = y.
Since x = y, we see that
2 y = y.
Thus 2 = 1, since we started with y nonzero.
Subtracting 1 from both sides,
1 = 0.

16. Activity: Monty Hall Problem
• Would you like to play a
game?
– In one of the three cups,
there is 5 dollar bill.
– In two of the three cups,
there is a “goat”
1. Select a cup
2. After revealing an
empty cup, you may
either change your
original choice, or keep
it.
3. Did you win?

17. How might we “prove” this?
• Let’s run a quick
experiment of
“exhaustion” of this
probability theorem.
• With a partner,
complete two sets of 10
guesses.
– One partner ALWAYS
changes cups
– One partner NEVER
changes cups.
• Who wins more?
http://blogs.discovermagazine.com/notrocketscience/2010/04/02/pigeons-outperform-
humans-at-the-monty-hall-dilemma/#.UWCwXpPCZ8E

18. Activity: Color Theorem
• Draw 5 shapes,
overlapping so as to create
various fields of space.
• Begin numbering so as to
do two things:
– Have the least amount of
numbers
– Never have one number
share a border with another.
• What is the least amount of
numbers needed?

20. Math across Cultures
• Language
– Integers and numerals
based in India and
Islamic civilization
– Consider “quipu” which
records numbers on
knotted strings.
– Consider imaginary
numbers, e, or pi as a
symbol corresponding to
reality or logic.
• What is the purpose of
our understanding of
numbers?

21. Math across Cultures
• Verification
– How may the
verification, or thought
process, change
between cultures?
– What may the result of
this diversity of
thinking result in
regarding theorems?

22. Math across Cultures
• Education
– Skills-Based or Inquiry
based?
– Differing methods of
teaching skills vs.
Inquiry
– Political dimension,
competition and
economy
– Value of the area of
knowledge in relation
to others.

23. Math and the Arts
• Math interacts with the
philosophy of beauty
• Some would argue that
mathematical principles
are derived from a
pursuit of music, art,
etc.
• Consider the Fibonacci
sequence, how does it
operate in the world?
Why is it “harmonious”?

25. Intuition, Emotion, and Faith
• Many formulas, theorems
and theories concerning
the scope and nature of
Math seem partially based
on intuited “knowing”
(impartial)
• How does the intuition of
order and consistency of
axioms relate to
presuppositions about God,
faith, Platonic “realms of
ideas” etc.?

26. Reading Discussion
• Informal Socratic Seminar
(20 minutes)
– Summarize your notes into
three main points (don’t just
repeat a fact, make a general
observation).
– Present an answer to the
following question:
• In what ways is mathematics
important to society?
– Write one question to present
to the class

27. 3 Ideas for the Week
• Statistical data is the
interaction between
– Science (what we look at)
– Math (how we look)
– Epistemology (why we look)
• Math is a counterweight to
expectation and intuition
• Our response to
mathematical choices reveal
underlying risk behavior.

28. Intro to Statistics: Climate Change
Figure 1: Berkeley Earth Surface Temperature (BEST) land-only surface temperature data (green) with
linear trends applied to the timeframes 1973 to 1980, 1980 to 1988, 1988 to 1995, 1995 to 2001, 1998 to
2005, 2002 to 2010 (blue)

29. Figure 2: Berkeley Earth Surface Temperature (BEST) land-only surface temperature data (green)
with linear treneds applied from 1973 to 2010 (red).

30. Figure 3: Berkeley Earth Surface Temperature (BEST) land-only surface temperature data (green) with linear trends applied to the
timeframes 1973 to 1980, 1980 to 1988, 1988 to 1995, 1995 to 2001, 1998 to 2005, 2002 to 2010 (blue), and 1973 to 2010 (red).

31. What makes a “good” statistical
reading?
• How does one collect data so as
to:
– Maintain ethical integrity?
– Reflect the “real world”?
– Answer your goals regarding
science?
– Avoid mistakes of history?
• How does one interpret data such
that:
– Bias is reduced?
– Understanding is progressing?
– Dialogue is maintained?
• How does this use of data relate
to the following:
– Ethics
– History
– Emotion
– Reason
– Language

32. Activity: Monty Hall Problem
• Would you like to play a
game?
– In one of the three cups,
there is 5 dollar bill.
– In two of the three cups,
there is a “goat”
1. Select a cup
2. After revealing an
empty cup, you may
either change your
original choice, or keep
it.
3. Did you win?

33. How might we “prove” this?
• Let’s run a quick
experiment of
“exhaustion” of this
probability theorem.
• With a partner,
complete two sets of 10
guesses.
– One partner ALWAYS
changes cups
– One partner NEVER
changes cups.
• Who wins more?
http://blogs.discovermagazine.com/notrocketscience/2010/04/02/pigeons-outperform-
humans-at-the-monty-hall-dilemma/#.UWCwXpPCZ8E

34. What is the Math?

35. On Wednesday
• Discussion question:
– Come to class with a
statistics or probability
problem related to your
Extended Essay topic
– Discuss how the
competing views of the
data affect your position
or understanding.
– Write 3 questions about
your topic as it might
relate to math.