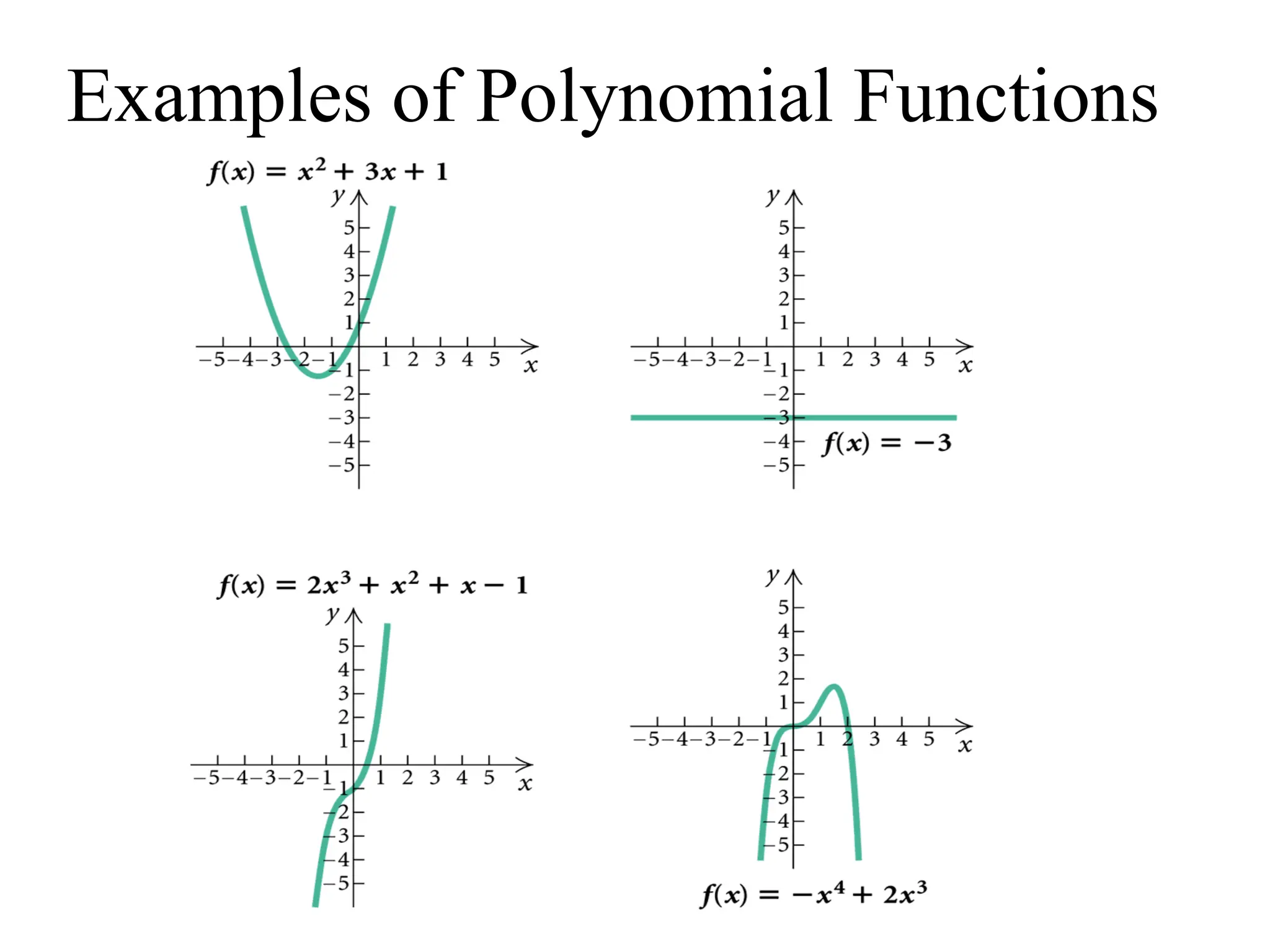
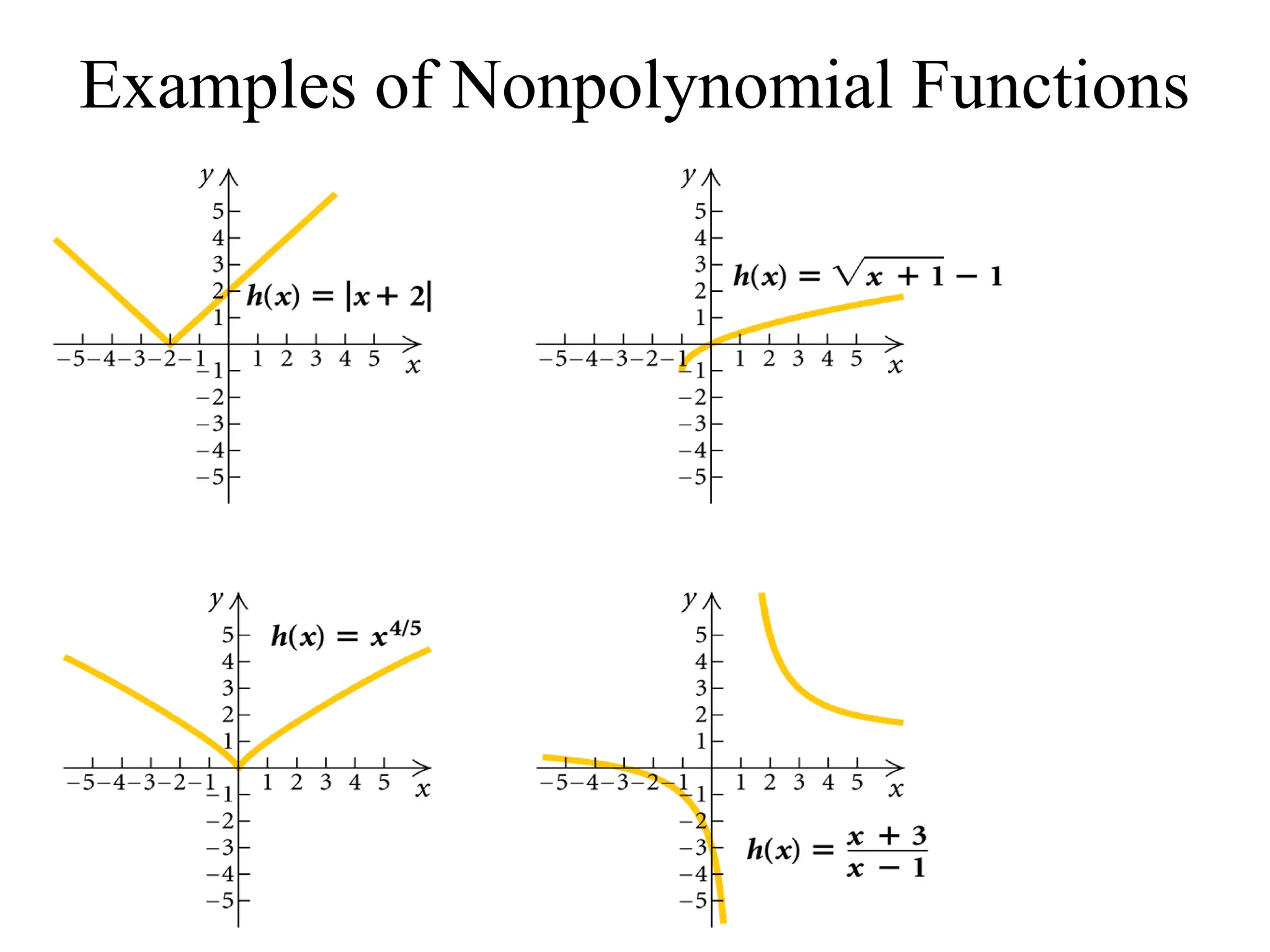
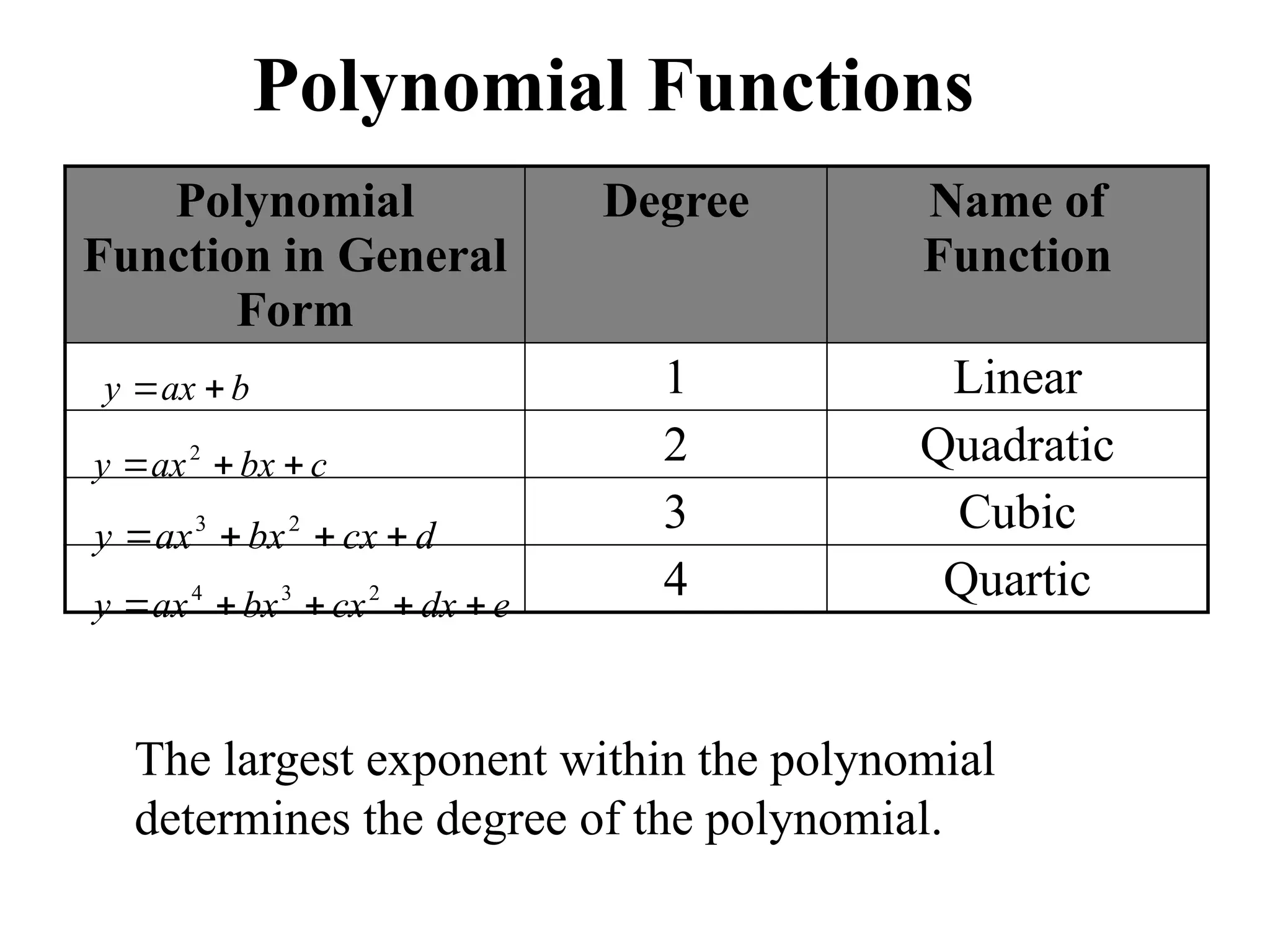
A polynomial is either a monomial or a sum of monomials, represented in functions with terms in descending order of exponents. The degree of a polynomial indicates its highest exponent, with specific names for degrees such as linear (1), quadratic (2), cubic (3), and quartic (4). The document also discusses identifying polynomial functions, determining their degree and leading coefficients, and provides examples of both polynomial and non-polynomial functions.

1. Polynomial
Functions

2. POLYNOMIAL FUNCTIONS
A POLYNOMIAL is a monomial
or a sum of monomials.
A POLYNOMIAL IN ONE
VARIABLE is a polynomial that
contains only one variable.
Example: 5x2
+ 3x - 7

3. A polynomial function is a function of the form
f(x) = an xn
+ an – 1 xn – 1
+· · ·+ a1 x + a0
Where an  0 and the exponents are all whole numbers.
A polynomial function is in standard form if its terms are
written in descending order of exponents from left to right.
For this polynomial function, an is the leading coefficient,
a0 is the constant term, and n is the degree.
an  0
an
an
leading coefficient
a0
a0
constant term n
n
degree
descending order of exponents from left to right.
n n – 1

4. POLYNOMIAL FUNCTIONS
The DEGREE of a polynomial in one variable is
the greatest exponent of its variable.
A LEADING COEFFICIENT is the coefficient
of the term with the highest degree.
What is the degree and leading
coefficient of 3x5
– 3x + 2 ?

5. POLYNOMIAL FUNCTIONS
A polynomial equation used to represent a
function is called a POLYNOMIAL FUNCTION.
Polynomial functions with a degree of 1 are called
LINEAR POLYNOMIAL FUNCTIONS
Polynomial functions with a degree of 2 are called
QUADRATIC POLYNOMIAL FUNCTIONS
Polynomial functions with a degree of 3 are called
CUBIC POLYNOMIAL FUNCTIONS

6. Degree Type Standard Form
You are already familiar with some types of polynomial
functions. Here is a summary of common types of
polynomial functions.
4 Quartic f (x) = a4x4
+ a3x3
+ a2x2
+ a1x + a0
0 Constant f (x) = a0
3 Cubic f (x) = a3x3
+ a2 x2
+ a1x + a0
2 Quadratic f (x) = a2 x2
+ a1x + a0
1 Linear f (x) = a1x + a0

7. Polynomial Functions
The largest exponent within the polynomial
determines the degree of the polynomial.
Polynomial
Function in General
Form
Degree Name of
Function
1 Linear
2 Quadratic
3 Cubic
4 Quartic
e
dx
cx
bx
ax
y 



 2
3
4
d
cx
bx
ax
y 


 2
3
c
bx
ax
y 

 2
b
ax
y 


8. Identifying Polynomial Functions
Decide whether the function is a polynomial function. If it is,
write the function in standard form and state its degree, type
and leading coefficient.
f(x) = x2
– 3x4
– 7
1
2
SOLUTION
The function is a polynomial function.
It has degree 4, so it is a quartic function.
The leading coefficient is – 3.
Its standard form is f(x) = –3x4
+ x2
– 7.
1
2

9. Decide whether the function is a polynomial function. If it is,
write the function in standard form and state its degree, type
and leading coefficient.
Identifying Polynomial Functions
The function is not a polynomial function because the
term 3
x
does not have a variable base and an exponent
that is a whole number.
SOLUTION
f(x) = x3
+ 3
x

10. Identifying Polynomial Functions
Decide whether the function is a polynomial function. If it is,
write the function in standard form and state its degree, type
and leading coefficient.
SOLUTION
f(x) = 6x2
+ 2x
–1
+ x
The function is not a polynomial function because the term
2x–1
has an exponent that is not a whole number.

11. Identifying Polynomial Functions
Decide whether the function is a polynomial function. If it is,
write the function in standard form and state its degree, type
and leading coefficient.
SOLUTION
The function is a polynomial function.
It has degree 2, so it is a quadratic function.
The leading coefficient is
.
Its standard form is f(x) = x2
– 0.5x – 2.
f(x) = – 0.5x + x2
– 2

12. f(x) = x
2
– 3x
4
– 7
1
2
Identifying Polynomial Functions
f(x) = x
3
+ 3x
f(x) = 6x
2
+ 2x
–1
+ x
Polynomial function?
f(x) = –0.5x + x2
– 2

13. POLYNOMIAL FUNCTIONS
EVALUATING A POLYNOMIAL FUNCTION
Find f(-2) if f(x) = 3x2
– 2x – 6
f(-2) = 3(-2)2
– 2(-2) – 6
f(-2) = 12 + 4 – 6
f(-2) = 10

14. POLYNOMIAL FUNCTIONS
EVALUATING A POLYNOMIAL FUNCTION
Find f(2a) if f(x) = 3x2
– 2x – 6
f(2a) = 3(2a)2
– 2(2a) – 6
f(2a) = 12a2
– 4a – 6

15. POLYNOMIAL FUNCTIONS
EVALUATING A POLYNOMIAL FUNCTION
Find f(m + 2) if f(x) = 3x2
– 2x – 6
f(m + 2) = 3(m + 2)2
– 2(m + 2) – 6
f(m + 2) = 3(m2
+ 4m + 4) – 2(m + 2) – 6
f(m + 2) = 3m2
+ 12m + 12 – 2m – 4 – 6
f(m + 2) = 3m2
+ 10m + 2

16. POLYNOMIAL FUNCTIONS
EVALUATING A POLYNOMIAL FUNCTION
Find 2g(-2a) if g(x) = 3x2
– 2x – 6
2g(-2a) = 2[3(-2a)2
– 2(-2a) – 6]
2g(-2a) = 2[12a2
+ 4a – 6]
2g(-2a) = 24a2
+ 8a – 12

17. Examples of Polynomial Functions

18. Examples of Nonpolynomial Functions