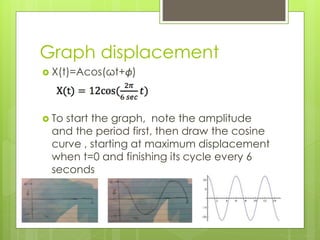
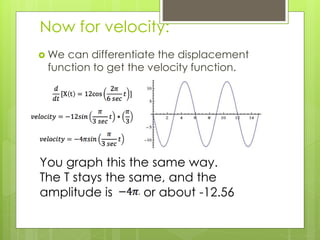
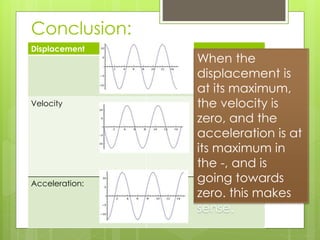
1) The document describes an object on a frictionless spring performing simple harmonic motion, oscillating with an amplitude of 12 meters over a period of 6 seconds. 2) Key values like the mass, amplitude, period, and angular frequency are determined from the description and used to derive the equations of motion. 3) The displacement, velocity, and acceleration as a function of time are determined by taking the derivative of each function, and graphs of each are drawn based on the simple harmonic motion equation and known values.

1. Determining
the equation
for simple
harmonic
motion of an
object on a
spring Itai Buxbaum
LD2
2/1/15

2. The situation:
 In your sleep, you dream that you have
invented a special, frictionless spring
mechanism, where no energy is being lost to
friction (thermal energy).
 As you wake up, you remember that the 2.0
kg object on the spring would move 12
meters from the equilibrium point, then return,
and continue 12 meters past the equilibrium
point in the other direction! It took 6 seconds
for this period to complete its cycle.
 Luckily remember that in PHYS 101 you
learned about SHM and now you decide that
you want to graph the functions for velocity
displacement and acceleration!

3. Game plan: what do we need
to figure out?
 We will need to find:
 The period, T and frequency, f
 the angular frequency ω
 A graph of the displacement of the object
 A graph of the velocity of the object
 And a graph of the acceleration of the
object

4. What do you remember? Lets
parse what we know into
physics terms…
The mass of the object
was 2 kg
m=2 kg
The max displacement
was 12m
Amplitude, A= 12
It took 6 seconds to
complete the period
Period, T= 6
No energy was lost due
to friction
Cool!

5. Step 2.
lets get to it!
 Lets start with angular frequency ω, the
magnitude of the angular velocity!

We know that T, period is 6 seconds so

6. Step 3. Put it into a function:
 The displacement function for Simple
Harmonic Motion looks like this:
 X(t)=Acos(ωt+ϕ)
 ϕ will be zero because we will start x(0)
with maximum displacement.
 Lets plug in what we have figured out and
then graph it:

7. Graph displacement
 X(t)=Acos(ωt+ϕ)
 To start the graph, note the amplitude
and the period first, then draw the cosine
curve , starting at maximum displacement
when t=0 and finishing its cycle every 6
seconds

8. Now for velocity:
 We can differentiate the displacement
function to get the velocity function.
You graph this the same way.
The T stays the same, and the
amplitude is or about -12.56

9. For acceleration:
 We can differentiate the velocity function
to get the acceleration function.

10. Conclusion:
Displacement
Velocity
Acceleration:
When the
displacement is
at its maximum,
the velocity is
zero, and the
acceleration is at
its maximum in
the -, and is
going towards
zero. this makes
sense.