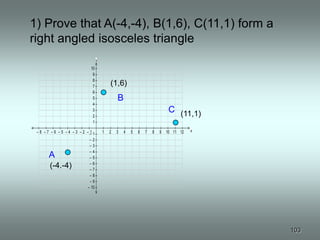
Here are the steps to solve this revision exercise: 1. Use the distance formula to find the lengths of each side: a) AB = √(−1 − 2)2 + (4 − 3)2 = 3.16 b) BC = √(1 − (−1))2 + (−3 − 4)2 = 7.28 c) AC = √(1 − 2)2 + (−3 − 3)2 = 6.08 2. Use the midpoint formula to find the midpoints of each side: a) MPAB = (0.5, 3.5) b) MPBC = (0, 0.5) c) MPAC = (

1. Unit 4 Coordinate Geometry
Starters
 Lesson 1: Midpoint of a line  Lesson 8: Perpendicular
and distance between 2 Lines
points  Lesson 9: Collinear points
 Lesson 2: To find the and drawing lines
gradient of a line  Lesson 10:Intercept –
 Lesson 3: Gradient of a line intercept method
making an angle with the  Lesson 11: Simultaneous
axes Equations
 Lesson 4: Rearranging the  Lesson 12/13:
equation of a straight line Simultaneous Equations-
 Lesson 5/6: Finding the Substitution
equation of lines from  Lesson 14/15:
given information Applications
 Lesson 7: Parallel Lines 1

2. Co-ordinate Geometry
Lesson 1
Midpoint of a line and distance
between 2 points
2

3. To find the mid point of a line
Midpoint of a line
A line segment is part of a line
y
10
The mid point is exactly half way between
the end points (x2,y2)
8
( x1 x2 ) ( y1 y2 )
mp ,
2 2 6
ie we average the points
4
In the example
2
x1 , y1 ( 4, 0), x2 , y2 0,8 (x1,y1)
–8 –6 –4 –2 x
( x1 x2 ) ( y1 y2 )
mp , –2
2 2
( 4 0) (0 8)
mp ,
2 2
mp 2, 4
3

4. Midpoint of a Line
The midpoint of the line joining two points (x1,y1) and (x2,y2) is
.
( x1 x2 ) y1 y2
,
2 2 ( x1 , y1 )
4

5. Be careful when there are negatives
x1 y1 x2 y2 It is useful to
put the correct
x1 , y1 (6, 1), x2 , y2 2, 3 coordinate over
the top then you
( x1 x2 ) ( y1 y2 ) won’t get
mp , confused
2 2
(6 2) ( 1 3)
mp ,
2 2
(6 2) ( 1 3)
mp ,
2 2
4 ( 4)
mp ,
2 2
mp 2, 2
5

6. Sometimes you are given the midpoint
Mid point of AB is (4,5) If A is (2,9) find B
A x1 , y1 (2,9), B x2 , y2 ( x, y ), mp 4,5
(2 x) (9 y )
(4,5) ,
2 2
(2 x) (9 y )
4 , 5
2 2
8 2 x, 10 9 y
x 6, y 1
B (6,1)
6

7. Calculate the midpoint of the lines joining the following
pairs of points;
1. (9 , 4) and (6 , 2)
2. (3 , 7) and (-4 , -1)
3. (-1 , 5) and (0 , -4)
4. (-5 , 7) and (5 , -7)
5. (-2 , -4) and (3 , -6)
6. (3.7 , -1.8) and (-2.4 , 1.5)
7. (x , 2x) and (-x , -2x)
8. (p , 0) and (-p , -p)
9. (z,- 3 z) and (-z, 3 z)
7

8. Ex 2.1: #1a-I (1column) 2-5
WB P170#12-25
(15mins)
8

9. Distance between two points
We can find the distance between two points by Pythagoras
y
8
2 2 2
h a b (x2,y2)
7
x 6
2 2 2
d ( x2 x1 ) ( y2 y1 ) 5
(y2-y1)
4
2 2
d ( x2 x1 ) ( y2 y1 ) 3
(x1,y1)
x 2
(x2-x1)
1
–8 –7 –6 –5 –4 –3 –2 –1 1 x
–1
x1 y1 x2 y2
( x1 , y1 ) ( 8,2) ( x2 , y2 ) ( 2,6)
9

10. Distance between two points
We can find the distance between two points by Pythagoras
2 2 2
y
h a b 8
d2 ( x2 x1 ) 2 ( y2 y1 ) 2 7
(x2,y2)
d ( x2 x1 ) 2 ( y2 y1 ) 2 x 6
5
2 2
d ( x2 x1 ) ( y2 y1 ) (y2-y1)
4
d (( 2) ( 8)) 2 (6 2) 2 (x1,y1) 3
x 2
(x2-x1)
d ( 2 8) 2 (4) 2 1
x
d (6) 2 (4) 2 –8 –7 –6 –5 –4 –3 –2 –1
–1
1
d 36 16
x1 y1 x2 y2
d 52 ( x1 , y1 ) ( 8,2) ( x2 , y2 ) ( 2,6)
d 7.2(1dp )units
10

11. Calculate the distance between the following points;
1. (9 , 4) and (6 , 2) = 3.6 units
2. (3 , 7) and (-4 , -1) = 10.6 units
3. (-1 , 5) and (0 , -4) = 9.1 units
4. (-5 , 7) and (5 , -7) = 17.2 units
5. (-2 , -4) and (3 , -6) = 5.4 units
6. (3.7 , -1.8) and (-2.4 , 1.5) = 6.5 units
7. (x , 2x) and (-x , -2x) 20 x units
8. (p , 0) and (-p , -p) 5 p units
9. (z,- 3 z) and (-z, 3 z) = 4z units
11

12. Remember
13 25
5
7
5
3
4 12 24
12

13. End of Lesson 1
Ex 2.2: #a-j odd, 2,3,4,5,7,8,9
WB P168 #1-11
13

14. Lesson 2
To find the gradient of a line
14

15. To find the gradient of a line
y
Gradient m 10 (x1,y1)
y 8
m
x 6
( y2 y1 ) 4
m
( x2 x1 ) 2
–8 –6 –4 –2 x
In the example –2
x1 y1 x2 y2 (x2,y2)
x1 , y1 ( 4,0), x2 , y2 0,8
(8 0)
m
(0 ( 4))
8
m
4
m 2
15

16. Be careful when there are negatives
x1 y1 x2 y2
x1, y1 ( 9, 3), x2 , y2 1, 4
( y2 y1 ) Sometimes we have unknowns
m The gradient of the line between
( x2 x1 )
(4, 2) and ( p,5) is p - 6. Find p
(( 4) ( 3))
m (5 2)
(( 1) ( 9)) p 6
( p 4)
( 4 3)
m ( p 4)( p 6) 3
( 1 9)
p 2 10 p 24 3
1
m p 2 10 p 21 0
8
( p 7)( p 3) 0
p 7, p 3
16

17. End of Lesson 2
WB P174 #26-35
Ex 2.3: # 2-9
17

18. Lesson 3
Gradient of a line making an
angle with the axes
18

19. To find the Gradient of a line making an angle θ
with the x axis
O y y2 y1
tan Gradient = m
A x x2 x1
2– 2
10
8
6
4
–2 O
8
6
4 y2 y1
tan m A
tan
x2 x1
In the example y
x1 y1 x2 y2 10
x1 , y1 ( 4,0), x2 , y2 0,8 (x2,y2) 8
(8 0) 6
Tan
(0 ( 4)) 4 O
8 2
Tan (x1,y1)
4 –8 –6 –4 –2 x
Tan 2 A
–2
Tan 1 (2) 63.4 (1dp ) 19

20. eg find the angle 2a line with the gradient of – ¾
2–
10
8
6
4
2– 2
10
8
6
4
makes with the positive direction of the x axis
3
Tan 10
y
4
8
1 3
tan 6
4
4
36.9
2
36.9 143.1
smallest angle is 36.9°
– 2 2 4 6 8 10 x
– 2
Largest angle is 36.9 180 143.1
20

21. Eg Ex 2.4
1. Calculate the gradient of a line making the following
angle with the positive direction of the x-axis
a) 240
tan 24 0.4452 gradient
b) 1260
tan126 1.376 gradient
3. Calculate angle line makes with positve x axis
given gradient is 3
gradient 3
tan 3 Note gradient undefined
1 tan
tan 3 1
tan (shift tan 9999999)
60
90
21

22. End of Lesson 3
Ex 2.4: #1 odd, 2 all, 3 odd, 4 -7
22

23. Lesson 4
Rearranging the equation
of a straight line
23

24. Rearranging the equation of a straight line
If a line is written in the form y mx c
Gradient y -intercept
Eg Ex 2.5 #1
Find the gradient of
2 y 3x 2 0 There are two forms for straight lines
We need to make y the subject
ax by c 0
2 y 3x 2 0 and
2 y 3x 2 y mx c
2 3 2
y x ( all of both sides by 2)
2 2 2
3
y= x 1
2
3
we can now see the gradient is and the y intercept is -1
2 24

25. eg 5 y 3 x 35 0
5y 3 x 35 ( all of both sides by 5)
5 5 5
-3
y x 7
5
-3
we can now see the gradient is and the yintercept is -7
5
From this we can now find the angle the line makes with the x axis
3
tan =- 31 180
5
1 3 149
tan -
5
( tells us angle angle with Positive direction
30.96
of the x axis going counter clockwise is 1490 )
31
25

26. The other form of the straight line is
ax by c o
Everything on one side =0
x is positive
no fractions
Rules to convert y mx c to ax by c 0
get rid of fractions
- whole numbers over 1
- bottoms the same
- multiply both sides by the bottom
put x on the side where it is positive
everything else on that side as well, other side =0
26

27. Eg
x 3
y
4 5
20 5 x 4 3
y
20 5 4 4 5
20 y 5 x 12
20 20 20
20 y 5 x 12
5 x 20 y 12
5 x 20 y 12
27

28. End of Lesson 4
Ex 2.5: 1k-p, 2-5
Ex 2.6: all
28

29. Lesson 5 & 6
Finding the equation of
lines from given
information
29

30. Revision Exercise
A (2,3),
B(-1,4) and 1. a) 3.16 b) 7.28
C(1,-3) form the c) 6.08
vertices of a
triangle. 2. a) (0.5 , 3.5) b) (0 , 0.5)
c) (1.5 , 0)
Find the
1. lengths,
3. a) -0.33 b) -3.5
2. midpoints and
3. gradients of all c) 6
three lines (sides)
in the triangle.
30

31. Finding the equation of lines from given information
y
10
( y y1 ) ( x2 , y2 )
m 8
( x x1 )
6
( x x1 )m ( y y1 )
4
( y y1 ) m( x x1 ) 2– 2
10 10
8 8
6 6
4 4
2– 2
6 6
4 4 ( x1 , y1 ) 2
We can find the equation given
–8 –6 –4 –2 x
3 combinations of information 2
–2
1)If we know the gradient (m) and one point (x1,y1) y
10
m 3, point(2,5) 8
( y y1 ) m( x x1 ) 6
4
( y 5) 3( x 2) 2
y 5 3x 6 –6 –4 –2
–2
2 4 6 x
–4
3x y 1 0
–6
or y 3x 1 –8
– 10 31

32. 2
eg Find the equation of the line with a gradient of that
5
passes through ( 3,4)
2
m , point(-3,4)
5
( y y1 ) m( x x1 )
2
( y 4) ( x ( 3)) 5 2 14
5 or y x
2 5 5 5
y 4 ( x 3)
5 5y 2 x 14
2 6
y 4 x
5 5 2 x 5 y 14 0
2 14
y x
5 5
32

33. 2) If you are given two points then you can find the gradient first,
then do as 1 above x1 y1 x2y2
eg
Find the equation of the line that passes through (4,1) and (7,3)
y2 y1 3 1 2
m m m
eg(7,3) x2 x1 7 4 3
First find
( y y) m( x Then the either
x1 ) using
point and or (4,1) ( y y1 ) m( x x1 )
2 gradient
( y 3) ( x y7) y1 m( x x1 ) 2
3 ( y 1) ( x 4)
2 14 3
y 3 x 2 8
3 3 y 1 x
2 5 3 2 5 3 3
y x or y x
3 3 2 5
3 3 3 y x
3y 2x 5 3 3
2x 3y 5 0
We would get the same answer if we used either point 33

34. 3) A (2,3), B(-1,4) and C(1,-3) form the vertices of a
triangle.
Find the equations of all three lines in the triangle.
34

35. 4) If we are given the angle with the x axis and a point. This is similar to being
given the gradient (Extn)
Eg A line passes through (3,4) and makes an angle of 63.4 with the
positive direction of the x axis
( y y1 ) m( x x1 )
tan 63.4 m
y 4 2( x 3)
m 2
y 4 2x 6
y 2x 2
2x y 2 0
Summary: We can find the equation of a straight line given
1) gradient (m) and one point ( x1 , y1 )
2) two points, then you can find the gradient first, then do as 1 above
3) the angle with the x axis and a point.
35

36. End of Lesson 5 & 6
Ex 2.7: all
WB P178 #36-51
Ex 2.8: 1h,I,j, 2all, 3-6
Ex 2.9: all
36

37. Lesson 7
Parallel Lines
37

38. Parallel Lines
Parallel Lines
Are always the same distance apart
Never meet
If a line is written in the form y mx c
2– 2
10 10
8 8
6 6
4 4
2– 2
10 10
8 8
6 6
4 4
We can see Gradient y -intercept
If lines have the same gradient then they are parallel y
10
y 2 x 6 is parallel to y 2x 1 8
6
4
2
Any line with a gradient
– 10 – 8 – 6 – 4 – 2 2 4 6 8 10 x
of 2 will be parallel to these – 2
– 4
– 6
– 8
– 10
38

39. If lines two lines y m1 x c and y m2 x c are parallel then m1 m2
Eg Find the line through (5,7) parallel to 3 y 4x 5 0
First make y the subject so line is in the form of
y mx c. Then we can see the gradient
3y 4x 5 0 4
( y 7) ( x 5)
3
3y 4x 5 4 20
4 5 y 7 x
y x 3 3
3 3 4 41
y x
4 3 3
m 3 4 41
3 or y x
then using point(5,7) 3 3 3
and 3y 4 x 41
(y y1 ) m( x x1 )
3 y 4 x 41 0 39

40. If a line through (3,4) and (6,a) is parallel to 4 x 2 y 5 0
Find "a"
If lines are parallel then they must have the same gradient
( y2 y1 )
m ,
4x 2 y 5 0 ( x2 x1 )
2y 4x 5 The gradient of the two
5 points will be the same
y 2x
2 (a 4)
m 2 2
(6 3)
a 4
2
3
6 a 4
a 10
40

41. End of Lesson 7
Ex 2.10: 2-7
41

42. Lesson 8
Perpendicular Lines
42

43. Perpendicular Lines
2– 2
10 10
8 8
6 6
4 4
2– 2
10 10
8 8
6 6
4 4
Perpendicular means: at right angles to
If lines are perpendicular then they are at right angles to each other
We know -ve
y 2x 4
+ve y
10
8
We can see these 6
lines are not 4
perpendicular 2
– 10 – 8 –6 –4 –2 2 4 6 8 10 x
–2
–4
–6
–8 y 2x 1
– 10
43

44. If two lines y m1 x c and y m2 x c are perpendicular
then
m1 m2 2– 2
10 10
8 8
6 6
4 4
2– 2
10 10
8 8
6 6
4 4 1
1 1
ie m1 and m2
m2 m1 y 2x 6
y
The gradients are negative reciprocals of each other yy
10
We can see these two 8
lines are perpendicular 6
4
Consider gradients of
2
x
– 10 –8 –6 –4 –2 2 4 6 8 10 xx
1 –2
m 2 and m -
2 –4
–6
1
y x 3 –8
2
– 10 44

45. Egs Ex 2.11
Find the gradient perpendicular to 3
-1
gradient is
3
7
Find the gradient perpendicular to
2
-2
gradient is
7
Find the gradient perpendicular to p
-1
gradient is
p
45

46. A (2,3), B(-1,4) and C(1,-3) form the
vertices of a triangle.
Find the equations of the
perpendicular bisectors of all three
lines
46

47. Egs Ex 2.11
Eg Find equation of a line through (-2,3) perpendicular to 3 y 4x 7 0
3y 4x 7 3 6
y 3 x
4 7 4 4
y x 4
3 3 m 3 3
3 y x
4 2
3
gradient 4 3 3 2
4 or y x
equation of perpendicular line is 4 4 2 2
(y y) m( x x1 ) 4y 3x 6
3 3x 4 y 6 0
( y 3) ( x ( 2))
4
3
y 3 ( x 2)
4
47

48. End of Lesson 8
Ex 2.11:#1-3,5-10 Extn 11-13
WB p182 # 52-59
48

49. Lesson 9
Collinear points and
Drawing lines
49

50. Collinear points and Drawing lines y
6
C
Collinear Points 4 (2,4)
Ie points on the same line 2
If points are on the same line, any two
–6 –4 –2 x
should give the same gradient 2 4 6
–2
B (0,-2)
–4
–6
y y1 –8
using m A
x x1 (-3,-11) – 10
– 12
( 2 ( 11)) ( 4 ( 11)) ( 4 ( 2))
mAB mAC mBC
(0 ( 3)) (2 ( 3)) (2 (0))
6
9 15
2
3 5
3 3
3
gradient of AB = gradient of AC = gradient of BC
50
So these points are collinear

51. NOTE: if points are collinear ie on the same line we can solve for an unknown
(2,1),( 3, q),(1, 2)are colinear so all points must meet the same equation
and have the same gradient
( y2 y1 ) ( y y1 ) m( x x1 )
m ,
( x2 x1 )
The gradient of any two point will be the same
( 2 1) ( 2 (q)) 2 q
m m 3
(1 2) (1 ( 3)) 4
2 q 2 q 12
3 m
m 1 3 q 14
1
2 q q 14
m 3 m
4
As points are collinear these gradients must be equal
51

52. Drawing lines:
To draw lines we need two pieces of information
1) 2 points- plot and join
2) 1 point and the gradient-plot point and use gradient
to find others
3) equation – either sub in x=1,2,3 etc
-or use gradient intercept
- or use intercept-intercept method
For Ex 2.13 we will rearrange in the form of y=mx+c to
establish the gradient and y intercept
52

53. End of Lesson 9
Ex2.12: all
Drawing Lines:
Ex 2.13 odd
WB P186 #64-75
WB P187 #76-81
53

54. Lesson 10
Intercept – intercept
method
54

55. Intercept – intercept method
1– 1
4
3
2 2
1– 1
6
5
4
3
2 2
If given the line in the form ax by c 0 it is easier to plot using this method
To find x intercept, put y = 0 Remember equation of x axis is y = 0
To find y intercept, put x = 0 equation of y axis is x = 0
y
Eg. 2x 3y 6 4
1)Cuts y axis put x 0
3
2(0) 3 y 6
2
3y 6
y 2 1
This gives us (0,2)
2)Cuts x axis put y 0 – 2 – 1 1 2 3 4 5 6 x
2 x 3(0) 6 –1
2x 6 –2
x 3
This gives us (3,0) 55

56. y
4
If given the graph
3
We can read the equation of the graph
2
1) gradient intercept method
1
2
y x 2
3 –2 –1 1 2 3 4 5 6 x
–1
2) Find gradient
–2
y2 y1
m Use gradient and point (3,0)
x2 x1
3 2 3
(0 2) ( y y) m( x x1 ) or y x 2
m 3 3 3
(3 0) 2
( y 0) ( x 3) 3y 2x 6
2 3
m 2 2x 3y 6 0
3 y x 2
3
56

57. End of Lesson 10
Ex 2.14all
Ex 2.15 all
57

58. Lesson 11
Simultaneous Equations
58

59. Simultaneous Equations
Simultaneous equations represent 2 lines on a graph that may intersect
We have three methods of finding the point of intersection
1) Graphing- either plot or use calculator
2) Elimination
3) Substitution (covered tomorrow)
59

60. 2)Elimination
Line up equations x over x
y over y
Sometimes we may need to rearrange to do this
Decide what to eliminate.
i.e. what number is, or can we get, the same
Do we need to add or subtract to eliminate?
7x y 1 1 7x y 1 4x 3y 3
4x 3y 3 2 7(0) y 1 4(0) 3( 1) 3
3 (7 x y 1) Multiply y 1
equation 1 Correct
by 3 to make the y
4 x 3 y First write out Now ytheysame are the Sub y=-1
3 termthe 1 terms
equations across same but have opposite back into the
21x 3 y 3
the page signs so we can add second
4x 3y 3 Sub x=0 back equation to
25 x 0 into equation Lines intersect at (0, 1)
check
1
x 0 60

61. Examples
3
y x 5 and y 2x 6
4
4 y 3x 25
2 y 5x 7
On Graphics Calculator either;
• Graph equations then - G-solve, intersect, Answer (4,2)
• Solve Simultaneous Equations in Equation Mode
* 61

62. 4x 7 y 20
10 x 5 y 25
*
62

63. Ex 2.18 #2
4x 2 3y
8
5 2
x 1 y 2
4
2 3
63

64. End of Lesson 11
Ex 2.17:1-17 odd
Ex 2.18 1-5 Extn all
64

65. Lesson 12 & 13
Simultaneous Equations
- Substitution
65

66. Simultaneous Equations
3) Substitution
If we know what x or y is, then in the second equation, we can put what
x or y is instead of writing x or y.
Hence we have the whole equation with only one variable.
Eg. y 5 4 x, 1 y 5 4 x, 10 x 7 y 1
10 x 7 y 1 2 y 5 4(2) 10(2) 7( 3) 1
10 x 7(5 4 x) 1 y 3 20 21 1
Sub
First write out Correct
10 x 35 28x equations acrossinto 2
1 1
the Now we can sub
y=-3 into the
18x 36 It is sensible to
page.
second equation
write the y= equation
x 2 first to check
Now we sub
x=2 back Point of intersection (2,-3)
into the first
equation
66

67. Example
y x 4
3x 2 y 2 0
* 67

68. Example
y 3x 9
4 x y 13
*
68

69. Example
y 2x 3
y x 9
*
69

70. Example
y 3x 1
y 3x 5
Lines have the same gradient
They are parallel.
No solution possible
*
70

71. End of Lesson 12 & 13
Ex 2.19 #1-15 odd Extn 16-18
Applications: Extra sheet
Ex 5.5 1-14 Extn all
71

72. Lesson 14 & 15
Applications of
Simultaneous Equations
72

73. End of Lesson 14 & 15
Applications:
Ex 2.20: 1-15 Extn all
Ex 16.17 sheet
RUR Q
Merit & Excellence Questions
WB P 192 #1-7
RUR Q
Exam Excellence Q 2.4 W/S
73

74. Starters
 Lesson 1  Lesson 9
 Lesson 2  Lesson 10
 Lesson 3  Lesson 11
 Lesson 4  Lesson 12
 Lesson 5  Lesson 13
 Lesson 6  Lesson 14
 Lesson 7  Lesson 15
 Lesson 8
74

75. Starter Lesson 1
Find the equation and list features
y
10
9
8
7
6
5
4
3
2
1
– 5 – 4 – 3 – 2 – 1 1 2 3 4 5 x
– 1
– 2
– 3
– 4
– 5
– 6
– 7
– 8
– 9
– 10
75

76. Answers Starter Lesson 1 y
10
9
8
7
6
5
4
3
2
1
– 5 – 4 – 3 – 2 – 1 – 1 1 2 3 4 5 x
– 2
– 3
– 4
– 5
– 6
– 7
– 8
– 9
– 10
y k ( x 1)( x 3)( x 5)
(0,-5)
Sub in (0, 5)
5 k ( 1)(3)(5)
1
5 15k y ( x 1)( x 3)( x 5)
3
1
k
3 76

77. y
Starter Lesson 2 10
9
8
7
6
5
1) Find the equation 4
3
and list features 2
1
– 5 – 4 – 3 – 2 – 1 – 1 1 2 3 4 5 x
– 2
– 3
– 4
– 5
– 6
– 7
– 8
– 9
– 10
2) Find the midpoint of A(-2,-5) B(3,1)
and the distance between the two points
3) Sketch the graph of y 2 x 1, x 3
77

78. 1)
10
9
y
Answers
Lesson 2
8
7
6
5
4
3
2
1
– 5 – 4 – 3 – 2 – 1 – 1 1 2 3 4 5 x
– 2
– 3
– 4
– 5
– 6
– 7
– 8
– 9
– 10
y k ( x 2)( x 1)( x 5)
(0,-4)
Sub in (0, 4)
4 k ( 2)(1)(5)
2
4 10k y ( x 2)( x 1)( x 5)
5
2
k
5 78

79. Answers Lesson 2
2)
A ( 2, 5), B (3,1)
x1 x2 y1 y2 d ( x2 x1 ) 2 ( y2 y1 ) 2
mp ,
2 2 ((3) ( 2)) 2 ((1) ( 5)) 2
2 3 5 1
, (3 2) 2 (1 5) 2
2 2
1 4 (5) 2 (6) 2
,
2 2 25 36
1 61
, 2
2 7.8(1dp)
79

80. Answers Lesson 2
y
8
7
6
5
4
3
2
1
– 3 – 2 – 1 1 2 3 4 5 6 x
– 1
– 2
– 3
– 4
– 5
y 2 x 1, x 3 We have a hole at x=3
80

81. Starter Lesson 3
1) Accurately sketch the graph 2x 1
y
x 5
That means properly
1) Cuts x axis y 0
2) Cuts y axis x 0
3)Vertical asymptote y
4) Horizontal asymptote x
2) What transformation maps y x2 9 onto y 9 x2
3) Sketch the graph of y 3x 5, x 2
81

82. Q1)
y
1) Cuts x axis y 0 15 2x 1
14
13 y
2x 1 0 12
11 x 5
10
9
2x 1 8
7
6
5
1 4
x 3
2
2 1
x
– 15– 14– 13– 12– 11– 10 – 9 – 8 – 7 – 6 – 5 – 4 – 3 – 2 ––11 1 2 3 4 5
– 2
2) Cuts y axis x 0 – 3
– 4
– 5
2(0) 1 – 6
– 7
y – 8
– 9
(0) 5 – 10
1
y 4) Horizontal asymptote x
5
2 1 2x
x
1
x
3)Vertical asymptote y y y x 5
5 x x
x 5 0 2 2
x 5 y y
1
y 2 y 2
82

83. 2) y
10
9
8
7
6
5
4
y x2 9
3
2
1
– 10 – 9 – 8 – 7 – 6 – 5 – 4 – 3 – 2 ––11 1 2 3 4 5 6 7 8 9 10 x
– 2
– 3
– 4
– 5
– 6
– 7 y 9 x2
– 8
– 9
– 10
Reflection in the x axis
83

84. y
10
9
8
7
6
5
4
3
2
1
– 5 – 4 – 3 – 2 – 1 – 1 1 2 3 4 5 x
– 2
– 3
– 4
– 5
– 6
– 7
– 8
– 9
– 10
– 11
– 12
– 13
– 14
– 15
y 3x 5, x 2 We have a hole at x = -2
84

85. Starter Lesson 4
1) Accurately sketch the graph
x 3
That means properly y
x 4
1) Cuts x axis y 0
2) Cuts y axis x 0
3)Vertical asymptote y
4) Horizontal asymptote x
2) What transformation maps y ( x 2)2 onto y ( x 2)2
3
3) Sketch the graph of y x 4, x 1
4
85

86. Q1)
y
15 x 3
14
13 y
1) Cuts x axis y 0 12
11 x 4
10
9
x 3 0 8
7
6
x 3 5
4
3
2
2) Cuts y axis x 0 1
x
– 15– 14– 13– 12– 11– 10 – 9 – 8 – 7 – 6 – 5 – 4 – 3 – 2 ––11 1 2 3 4 5
– 2
(0) 3 – 3
– 4
y – 5
(0) 4 – 6
– 7
– 8
– 9
3 – 10
y
4 4) Horizontal asymptote x
x 3
3 x x
3)Vertical asymptote y y y x 4
4 x x
x 4 0 1
x 4 y y
1
y 1 y 1
86

87. 2) y
10
9
8
7 y ( x 2) 2
6
5
4
3
2
1
–5 –4 –3 –2 – 1– 1 1 2 3 4 5 6 7 8 x
–2
–3
–4
–5
–6
–7 y ( x 2) 2
–8
–9
– 10
Reflection in the x axis
87

88. y
3
2
1
– 5 – 4 – 3 – 2 – 1 1 2 3 4 5 x
– 1
– 2
– 3
– 4
– 5
– 6
– 7
– 8
– 9
– 10
3 We have a hole at x = 1
y x 4, x 1
4
88

89. Starter Lesson 5
1) Accurately sketch the graph
2x 1
That means properly y
1) Cuts x axis y 0 x 4
2) Cuts y axis x 0
3)Vertical asymptote y
4) Horizontal asymptote x
List Features
2) Sketch the graph of y ( x 1)(3 x)( x 2)
89

90. Q1)
y
1) Cuts x axis y 0 15 2x 1
14
13
y
2x 1 0 12
11
x 4
10
9
2x 1 8
7
6
5
1 4
x 3
2
2 1
– 15– 14– 13– 12– 11– 10 – 9 – 8 – 7 – 6 – 5 – 4 – 3 – 2 ––11 1 2 3 4 5 x
2) Cuts y axis x 0 – 2
– 3
– 4
– 5
2(0) 1 – 6
– 7
y – 8
(0) 4 – 9
– 10
1
y 4) Horizontal asymptote x
4 2x 1
2 1 x x
y y x 4
3)Vertical asymptote y 4 x x
x 4 0 2 2
y y
x 4 1
y 2 y 2
90

91. Features
1
x intercept x
2
1
y intercept y
4
Vertical asymptote x 4
Horizontal asymptote y 2
fundemental discontinuity at x -4
point symmetry at (-4,2)
axis of symmetry y x 6, y x 2
x ,y 2
x ,y 2
91

92. y
8
7
6
5
4
3
2
1
– 5 – 4 – 3 – 2 – 1 1 2 3 4 5 x
– 1
– 2
– 3
– 4
– 5
– 6
– 7
– 8
– 9
– 10
y ( x 1)(3 x)( x 2)
92

93. Starter Lesson 6
1) Accurately sketch the graph
3x 4
That means properly y
1) Cuts x axis y 0 x 2
2) Cuts y axis x 0
3)Vertical asymptote y
4) Horizontal asymptote x
List Features
2) Sketch the graph of x 2 ( y 1) 2 25
List Features
93

94. Q1)
y
15 3x 4
1) Cuts x axis y 0 14
13
y
12
11
x 2
3x 4 0 10
9
8
3x 4 7
6
5
4
4 3
2
x 1
3 – 10 – 9 – 8 – 7 – 6 – 5 – 4 – 3 – 2 ––11
–2
1 2 3 4 5 6 7 8 9 10 x
–3
2) Cuts y axis x 0 –4
–5
–6
3(0) 4 –7
–8
y –9
– 10
(0) 2
y 2 4) Horizontal asymptote x
3x 4
3 4 x x
y y x 2
3)Vertical asymptote y 2 x x
x 2 0 3 3
y y
x 2 1
y 3 y 3
94

95. Features
4
x intercept x
3
y intercept y 2
Vertical asymptote x 2
Horizontal asymptote y 3
fundemental discontinuity at x -2
point symmetry at (-2,3)
axis of symmetry y x 5, y x 1
x ,y 3
x ,y 3
95

96. y
6
x2 ( y 1) 2 25 5
4
3
Centre(0,1) 2
Radius =5units 1
Y intercepts (0,6)and(0,- –5 –4 –3 –2 –1 1 2 3 4 5 x
–1
4)
–2
Max(0,6), Min(0,-4) –3
–4
–5
0
x2 y2 25 translated by
1
96

97. Q1)
Starter Lesson 7
Find the equation, and list features
y
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
–5 –4 –3 –2 –1 1 2 3 4 5 6 7 8 9 10 x
– 1
– 2
– 3
– 4
– 5
97

98. Features
x intercept x 4.6
2
y intercept y 7
3
Vertical asymptote x 3
Horizontal asymptote y 5
fundemental discontinuity at x 3
point symmetry at (3,5)
axis of symmetry y x 2, y x 8
x ,y 3
x ,y 3
98

99. 2)What transformation will map
x2 y2 1 on to the graph x 2 y 2 16
y
5
4
3
2
1
–5 –4 –3 –2 –1 1 2 3 4 5 x
–1
–2
–3
–4
–5
99

100. Image radius
SF
Object radius
4
SF
1
SF 4
Enlargement about (0,0) of scale factor 4
Must have
centre
100

101. 3) What transformation maps y x 2 on to y ( x 3)2 5
y
8
7
Translation by 6
5
3
the vector 4
-5 3
2
1
–5 –4 –3 –2 –1 1 2 3 4 5 6 7 x
–1
–2
–3
–4
–5
–6
101

102. Starter Lesson 8
1) Prove that A(-4,-4), B(1,6), C(11,1) form a
right angled isosceles triangle
102

103. 1– 1
10 10
9 9
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1– 1
12
11
10
9
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1) Prove that A(-4,-4), B(1,6), C(11,1) form a
right angled isosceles triangle
y
10
9
8
7 (1,6)
6
5 B
4
3 C (11,1)
2
1
–8 –7 –6 –5 –4 –3 –2 ––1
1 1 2 3 4 5 6 7 8 9 10 11 12 x
–2
–3
–4
A –5
–6
(-4.-4) –7
–8
–9
– 10
103

104. y y1
A( 4, 4), B(1,6), C (11,1) m
y x x1
10
6 ( 4) 9
(1,6)
mAB 8
7
1 ( 4) 6 B
5
10 4
3
2
5 1
(11,1)
2 –8 –7 –6 –5 –4 –3 –2 ––1
1 1 2 3 4 5 6 7 8 9 10 11 12 x C
–2
–3
–4
A –5
–6
1 6 (-4.-4) –7
mBC –8
11 1 –9
– 10
5
10 1
2 1 as gradients multiply to give -1
1 2
2 they are at right angles
104

105. d AB ( x x1 ) 2 ( y y1 ) 2 d AC ( x x1 ) 2 ( y y1 ) 2
d AB ( 4 1) 2 ( 4 6) 2 d AC ( 4 11) 2 ( 4 1) 2
d AB ( 5) 2 ( 10) 2 d AC ( 15) 2 ( 5) 2
d AB 25 100 d AC 225 25
d AB 125 d AC 250
Because 2 sides are equal and one
d BC ( x x1 ) 2 ( y y1 ) 2
is not equal, therefore the triangle is
d BC (1 11) 2 (6 1) 2 isosceles
d BC ( 10) 2 (5) 2 We proved before that AB is
Perpendicular to BC so this is a right
d BC 100 25 angled isosceles triangle
d BC 125
105

106. Starter Lesson 9
1)Find the equation of the line through
(9,1) and (4,7)
2)Find the equation of the line through
(3,2) and (3,10)
106

107. 1)Find the equation of the line through
(9,1) and (4,7)
y2 y1 Equation
m y y1 m( x x1 )
x2 x1
7 1 6
m y 1 ( x 9)
4 9 5
6 6 54
m y 1 x
5 5 5
6 59
y x
5 5
5y 6 x 59 0
107

108. 2)Find the equation of the line through
(3,2) and (3,10)
y2 y1
m
x2 x1
10 2
m
3 3
m undefined
We know lines with an undefined gradient
arevertical and so x
In this case x 3
108

109. Starter Lesson 10
1) Find the line through the point (5,4) parallel
to the line 3x y 2 0
3
2)Draw the lines y x 5
4
4
y x 2
3
3)Prove the above lines are perpendicular
109

110. 1) Find the line through the point (5,4) parallel
to the line 3x y 2 0
y 3x 2 gdt 3 pt (5, 4)
y y1 m( x x1 )
y 4 3( x 5)
y 4 3x 15
y 3x 11
110

111. 3
2)Draw the lines y x5
4
4
y x 2
3
3)Prove the above lines are perpendicula r
y
5
3 4
4 1
3
4 3
2
As gradients multiply to = -1
1
Lines are perpendicular
–5 –4 –3 –2 –1 1 2 3 4 5 x
–1
–2
–3
–4
–5
111

112. Starter Lesson 11
1) Find the equation of the line that passes
through (1,8) and (6,8)
2) Use the intercept- intercept method to plot
6x 4 y 3
3) Find the line through the point (1,4)
perpendicular to the line 4 x y 3 0
112

113. 1) Find the equation of the line that passes
through (1,8) and (6,8)
y2 y1
m
x2 x1
8 8
m Line has a gradient of zero so horizontal
6 1
0 y ?
m
5 both y coordinates are 8
m 0 y 8
113

114. 2) Use the intercept- intercept method to plot
6x 4 y 3 y
Cuts x axis y 0 5
6 x 4(0) 3 4
3
6x 3
2
3
x
6 1
1 x
x –5 –4 –3 –2 –1 1 2 3 4 5
2 –1
Cuts y axis x 0 –2
6(0) 4 y 3 –3
4y 3 –4
3 –5
y
4
114

115. 3) Find the line through the point (1,4) perpendicular
to the line 4 x y 3 0 1
m (1, 4)
4x 3 y 4
y 4x 3 y y1 m( x x1 )
m 4 1
y 4 ( x 1)
1 4
m 1 1
4 y 4 x
4 4
1 1 16
y x
4 4 4
1 17
y x
4 4
x 4 y 17 0
115

116. Lesson 12 Starter
1) Solve
2y x 2
5 x 2 y 10 0
3x 1
2) Sketch y
x 2
and list features
That means properly
1) Cuts x axis y 0
2) Cuts y axis x 0
3)Vertical asymptote y
4) Horizontal asymptote x
116

117. 1) Solve
2y x 2 5 x 2 y 10 0 2y x 2
5 x 2 y 10 0 5(3) 2 y 10 0 2(2.5) 3 2
15 2 y 10 0 5 3 2
x 2y 2 5 2y
true
5 x 2 y 10 y 2.5
4 x 12
(3, 2.5)
x 3 Checked on the
calculator of course
117

118. 3x 1 y
3x 1
2) Sketch y and list features 15
14 y
x 2 13
12 x 2
11
1) Cuts x axis y 0 10
9
8
7
3x 1 0 6
5
4
3x 1 3
2
1
1 – 15– 14– 13– 12– 11– 10 – 9 – 8 – 7 – 6 – 5 – 4 – 3 – 2 ––11
– 2
1 2 3 4 5 x
x – 3
– 4
3 – 5
– 6
– 7
2) Cuts y axis x 0 – 8
– 9
– 10
3(0) 1
y
(0) 2 4) Horizontal asymptote x
3x 1
1 3 1 x x
y y y x 2
2 2 x x
3)Vertical asymptote y 3 3
y y
x 2 0 1
x 2 y 3 y 3
118

119. Features
1
x intercept x
3
1
y intercept y
2
Vertical asymptote x 2
Horizontal asymptote y 3
fundamental discontinuity at x 2
point symmetry at (-2,3)
axis of symmetry y x 5, y x 1
x ,y 3
x ,y 3
119

120. Starter Lesson 13
1) Find the line perpendicular to 5 y 4 x 7 0 which
passes through the point (3,1)
2) If (3,4) (6,2) (8,a) are collinear
Find a
120

121. 1) Find the line perpendicular to 5 y 4 x 7 0 which
passes through the point (3,1)
5y -4 x 7
4 7
y x
5 5
4 5
m ,m
5 4
y y1 m( x x1 )
5
y 1 ( x 3)
4
5 11
y x
4 4
5 x 4 y 11 0
121

122. 2) If (3,4) (6,2) (8,a) are collinear
Find a
y2 y1
m if lines are collinear they have the same gdt
x2 x1
2 4 2 a 2
m
6 3 3 8 6
2 2 2 a 2 3
m
3 2 3 2 2
4 3(a 2)
4 3a 6
2 3a
2
a
3
122

123. Starter Lesson 14
1)Show that the line through (0,4) and (4,1) is
perpendicular to the line through (3,6) and (-3,-2)
2)Find the midpoint of A(4,2) and B(10,10)
123

124. 1)Show that the line through A(0,4) and B(4,1) is
perpendicular to the line through C(3,6) and D(-3,-2)
y2 y1 y2 y1
mAB mCD
x2 x1 x2 x1
1 4 2 6
mAB mCD
4 0 3 3
3 8
mAB mCD
4 6
4
mCD
3
as mAB mCD 1
3 4
1 lines are perpendicular
4 3
124

125. 2)Find the midpoint of A(4,2) and B(10,10)
( x1 x2 ) ( y1 y2 )
m ,
2 2
(4 10) (2 10)
m ,
2 2
14 12
m ,
2 2
m 7, 6
125

126. Starter Lesson 15
Prove that the points A(-3,7) B(9,15) C(5,-5)
form a right angled isosceles triangle
126

127. Prove that the points A(-3,7) B(9,15) C(5,-5) d AB ( x2 x1 ) 2 ( y2 y1 ) 2
form a right angled isosceles triangle d (9 ( 3)) 2 (15 7) 2
y d 122 82
18
17 d 208
16
15 B d AC ( x2 x1 ) 2 ( y2 y1 ) 2
14
13
12 d (5 ( 3)) 2 ( 5 7) 2
11
10 d 82 122
9
8
A 7 d 208
6
5 d BC ( x2 x1 ) 2 ( y2 y1 ) 2
4
3
2 d (9 5) 2 (15 ( 5) 2
1
– 5 – 4 – 3 – 2 – –1 1 1 2 3 4 5 6 7 8 9 10 x d 42 202
–2
–3 d 416
–4
–5
–6 C As two sides are the same and one is different,
–7
–8 this proves that the triangle is isosceles
127

128. y2 y1 y2 y1
mAB mAC
x2 x1 x2 x1
15 7 5 7
9 ( 3) 5 ( 3)
8 12
12 8
2 3
3 2
mAB mAC
2 3
3 2
1 ABis toAC
Triangle is a right angled isosceles
128