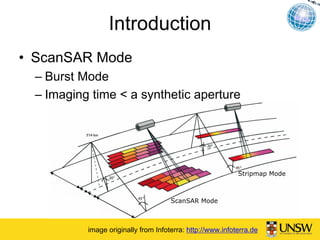
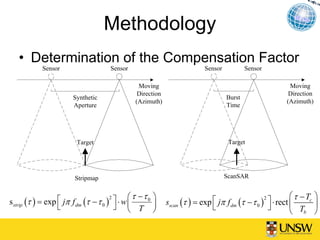
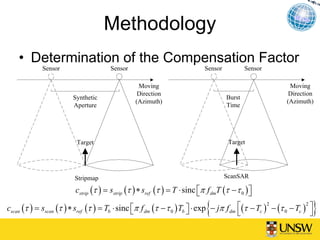
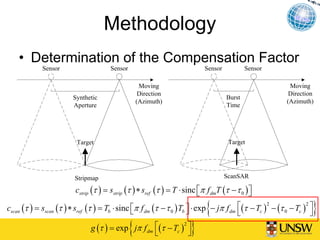
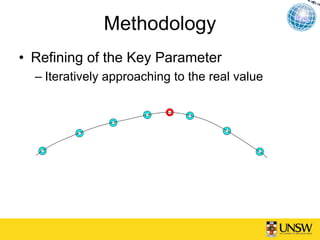
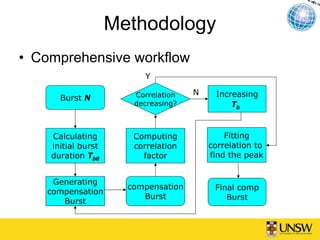
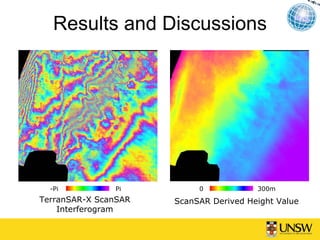
This document describes a method for blind azimuth phase elimination in TerraSAR-X ScanSAR interferometry. The method determines a compensation factor based on the differences between stripmap and ScanSAR imaging geometries. It then performs an iterative process to refine the key parameter of burst duration and generate a compensation burst to eliminate nonlinear azimuth phases. Results on a TerraSAR-X dataset show the method can provide ScanSAR interferograms and DEMs without azimuth distortions. The method provides a solution for interferometry using only ScanSAR SLC data.

1. Blind Azimuth Phase
Elimination for TerraSAR-X
ScanSAR Interferometry
Alex Zhe Hu, Linlin Ge and Xiaojing Li
Geodesy and Earth Observing Systems Group (GEOS),
School of Surveying and Spatial Information Systems,
The University of New South Wales, Sydney, Australia
Email: z.hu@student.unsw.edu.au

2. Contents
• Introduction
• Methodology
• Results and Discussions
• Concluding Remarks

3. Contents
• Introduction
• Methodology
• Results and Discussions
• Concluding Remarks

4. Introduction
• ScanSAR Mode
– Burst Mode
– Imaging time < a synthetic aperture
Stripmap Mode
ScanSAR Mode
image originally from Infoterra: http://www.infoterra.de

5. Introduction
• ScanSAR Mode
– Cover multiple swathes
– Large range coverage
Stripmap Mode
ScanSAR Mode
image originally from Infoterra: http://www.infoterra.de

6. Introduction
• ScanSAR Interferometry
– Cover multiple swathes
– Large range coverage
– Global DEM
– Large-scale Earthquakes

7. Introduction
• ScanSAR Interferometry
ALOS EnviSAT
RADARSAT TerraSAR-X
PALSAR ASAR
L-band C-band C-band X-band
250–350km 400km 300–500km 150km
100m 75–150m 50–100m up to 16m
Ortiz and Holzner and
Shimada 2007 ?
Zebker 2007 Bamler 2002

8. Introduction
• TerraSAR-X ScanSAR Interferometry
– Distortion and signal loss in azimuth direction
after resampling
– Only SLC data available for the public

9. Introduction
• TerraSAR-X ScanSAR Interferometry
– Distortion and signal loss in azimuth direction
after resampling
– Only SLC data available for the public
– Blind Azimuth Phase Elimination

10. Contents
• Introduction
• Methodology
• Results and Discussions
• Concluding Remarks

11. Methodology
• Phase Estimation Strategy
– The simulated burst for compensation should
have similar fringe patterns

12. Methodology
• Brief workflow
Determination of the
Compensation Factor
Coarse Initialisation of
the Key Parameter
Refining of
the Key Parameter
Elimination of
the Azimuth Phase

13. Methodology
• Determination of the Compensation Factor
Sensor Sensor Sensor Sensor
Moving Moving
Direction Direction
Synthetic Burst
(Azimuth) (Azimuth)
Aperture Time
Target Target
Stripmap ScanSAR
⎛ τ −τ 0 ⎞ ⎛ τ − Tc ⎞
s strip (τ ) = exp ⎡ jπ f dm (τ − τ 0 ) ⎤ ⋅ w ⎜ sscan (τ ) = exp ⎡ jπ f dm (τ − τ 0 ) ⎤ ⋅ rect ⎜
2 2
⎣ ⎦ ⎝ T ⎟ ⎣ ⎦ ⎟
⎠ ⎝ Tb ⎠

14. Methodology
• Determination of the Compensation Factor
Sensor Sensor Sensor Sensor
Moving Moving
Direction Direction
Synthetic Burst
(Azimuth) (Azimuth)
Aperture Time
Target Target
Stripmap ScanSAR
cstrip (τ ) = sstrip (τ ) ∗ sref (τ ) = T ⋅ sinc ⎡π f dmT (τ − τ 0 ) ⎤
⎣ ⎦
⎣ ⎦ {
cscan (τ ) = sscan (τ ) ∗ sref (τ ) = Tb ⋅ sinc ⎡π f dm (τ − τ 0 ) Tb ⎤ ⋅ exp − jπ f dm ⎡(τ − Tc ) − (τ 0 − Tc ) ⎤
⎣
2 2
}
⎦

15. Methodology
• Determination of the Compensation Factor
Sensor Sensor Sensor Sensor
Moving Moving
Direction Direction
Synthetic Burst
(Azimuth) (Azimuth)
Aperture Time
Target Target
Stripmap ScanSAR
cstrip (τ ) = sstrip (τ ) ∗ sref (τ ) = T ⋅ sinc ⎡π f dmT (τ − τ 0 ) ⎤
⎣ ⎦
⎣ ⎦ {
cscan (τ ) = sscan (τ ) ∗ sref (τ ) = Tb ⋅ sinc ⎡π f dm (τ − τ 0 ) Tb ⎤ ⋅ exp − jπ f dm ⎡(τ − Tc ) − (τ 0 − Tc ) ⎤
⎣
2 2
}
⎦
{
g (τ ) = exp jπ f dm ⎡(τ − Tc ) ⎤
⎣
2
⎦ }

16. Methodology
• Determination of the Compensation Factor
Sensor Sensor Sensor Sensor
Moving Moving
Direction Direction
Synthetic Burst
(Azimuth) (Azimuth)
Aperture Time
Target Target
Stripmap ScanSAR
{
g (τ ) = exp jπ f dm ⎡(τ − Tc ) ⎤
⎣
2
⎦ }
cscan (τ ) = ⎣ sscan (τ ) ∗ sref (τ ) ⎦ ⋅ g (τ ) = Tb ⋅ sinc ⎡π f dm (τ − τ 0 ) Tb ⎤ ⋅ exp ( jφ )
⎡ ⎤ ⎣ ⎦

17. Methodology
• Coarse Initialisation of the Key Parameter
g (τ ) = exp { jπ f dm ⎡(τ − Tc ) ⎤} = exp { jπ f dm ⎡(τ − Ts − Tb 2 ) ⎤}
2 2
⎣ ⎦ ⎣ ⎦
– The compensation factor is a function of burst
duration Tb

18. Methodology
• Coarse Initialisation of the Key Parameter
cscan (τ ) = sscan (τ ) ∗ sref (τ ) = F −1 { F ⎡ sscan (τ ) ⎤ ⋅ F ⎡ sref (τ ) ⎤}
⎣ ⎦ ⎣ ⎦
{ ⎣ ⎦ ⎣ }
= F −1 a ⋅ ⎡ S strip (ω ) ∗W (ω ) ⎤ ⋅ F ⎡ sref (τ ) ⎤
⎦

19. Methodology
• Coarse Initialisation of the Key Parameter
cscan (τ ) = sscan (τ ) ∗ sref (τ ) = F −1 { F ⎡ sscan (τ ) ⎤ ⋅ F ⎡ sref (τ ) ⎤}
⎣ ⎦ ⎣ ⎦
{ ⎣ ⎦ ⎣ }
= F −1 a ⋅ ⎡ S strip (ω ) ∗W (ω ) ⎤ ⋅ F ⎡ sref (τ ) ⎤
⎦
1
aTb
{ {
⋅ F −1 F F ⎡cscan (τ ) ⎤ F ⎡ sref (τ ) ⎤
⎣ ⎦ ⎣ ⎦ } ⎣ ⎦ }
F ⎡ S strip (ω ) ⎤ = sinc (Tbω )
– time difference between two peaks of sinc
function is determined by Tb

20. Methodology
• Coarse Initialisation of the Key Parameter

21. Methodology
• Refining of the Key Parameter
– Iteratively approaching to the real value

22. Methodology
• Comprehensive workflow
Y
Correlation N Increasing
Burst N
decreasing? Tb
Calculating Computing Fitting
initial burst correlation correlation to
duration Tb0 factor find the peak
Generating
compensation Final comp
compensation
Burst Burst
Burst

23. Contents
• Introduction
• Methodology
• Results and Discussions
• Concluding Remarks

24. Results and Discussions
Information Master Image Slave Image
Acquisition Date 16 February 2010 27 February 2010
Acquisition Start
02:56:12 (UTC) 02:56:13 (UTC)
Time
Acquisition Stop
02:56:30 (UTC) 02:56:31 (UTC)
Time
Number of
4 (strip_04 – strip_07)
Swathes
Number of Bursts 59 (strip_04 – strip_07) 61 (strip_04 – strip_07)
Central Latitude 28.785 ° 28.785 °
Central Longitude 47.514 ° 47.513°
Range Resolution 2.504 (metre) 2.503 (metre)
Azimuth
18.5 (metre) 18.5 (metre)
Resolution

25. Results and Discussions
Original Bursts

26. Results and Discussions
Original Bursts
Compensation Phases

27. Results and Discussions
Original Bursts
Compensation Phases
Bursts after azimuth phase elimination

28. Results and Discussions
Resampled slave Burst-based interferogram

29. Results and Discussions
-Pi Pi 0 300m
TerranSAR-X ScanSAR ScanSAR Derived Height Value
Interferogram

30. Results and Discussions
ScanSAR Derived DEM

31. Results and Discussions
-50 50m
Height difference to SRTM DEM Histogram of the difference

32. Contents
• Introduction
• Methodology
• Results and Discussions
• Concluding Remarks

33. Concluding Remarks
• Simplifying the TerraSAR-X ScanSAR
interferometry by making it Stripmap-like
• Precise enough to remove the non-linear
azimuth phases
• Providing a solution for TerraSAR-X
ScanSAR interferometry starts from SLC
data
• Can also be applied to other advanced
SAR system with non-linear azimuth
phases, such as Spotlight

34. Acknowledgement:
The authors are grateful to Infoterra for providing the
TerraSAR-X ScanSAR dataset on this research.
The first author also sincerely thanks GEOS and the Faculty of
Engineering of UNSW for supporting his scholarship on his PhD
study.