Документ описывает основы геометрии, включая понятия линий, углов, поверхностей и пространственных форм, таких как треугольники и квадраты. Он также рассматривает применение геометрии в реальном мире, инструменты для измерений, а также различные типы углов и их свойства. Важнейшими инструментами в геометрии являются линейка, циркуль и транспортир.










































































![[От редакции]
ГЕОМЕТРИЯ
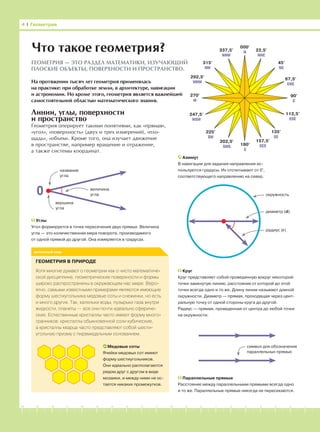
Что такое геометрия?
Линии, углы, поверхности
и пространство
Инструменты
в геометрии
Инструменты, используемые
в геометрии
Использование циркуля
Использование линейки
Другие инструменты
Использование транспортира
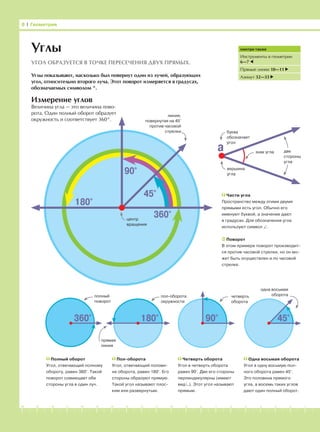
Углы
Измерение углов
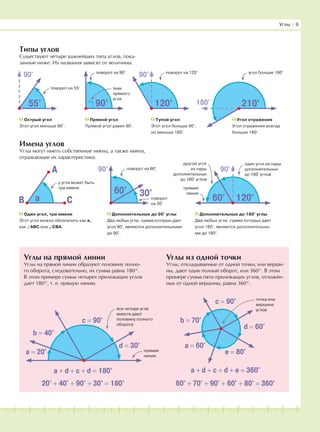
Типы углов
Имена углов
Углы на прямой линии
Углы из одной точки
Прямые линии
Точки, прямые и плоскости
Набор прямых
Углы и параллельные прямые
Проведение параллельной
прямой
Симметрия
Зеркальная симметрия
Плоскости симметрии
Вращательная симметрия
Оси симметрии
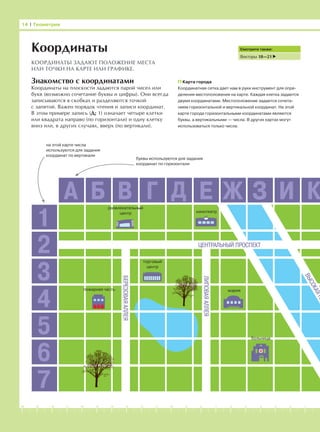
Координаты
Знакомство с координатами
Чтение карты
Использование координат
Содержание
Координаты графиков
Изображение координат
Уравнение прямой
Карта мира
Векторы
Что такое вектор?
Запись векторов
Направление векторов
Равные векторы
Модуль вектора
Сложение и вычитание векторов
Умножение векторов
Работа с векторами
в геометрии
Параллельный
перенос
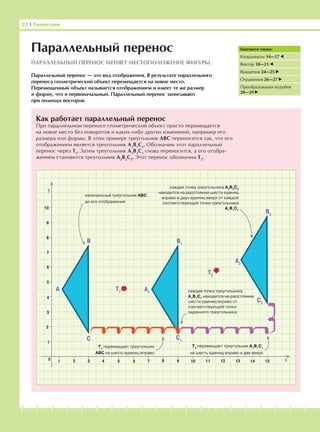
Как работает параллельный
перенос
Запись параллельного переноса
Направление переноса
Вращения
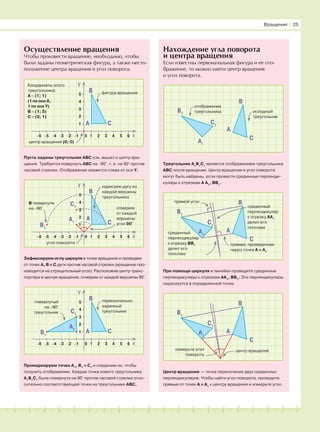
Свойства вращения
Осуществление вращения
Нахождение угла поворота
и центра вращения
Отражения
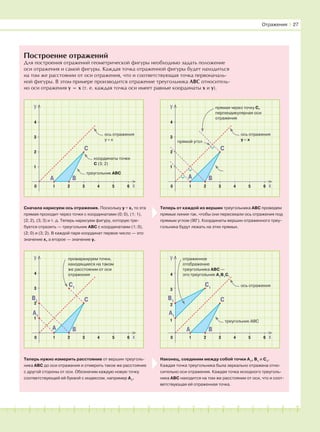
Свойства отражения
Построение отражений
Преобразования
подобия
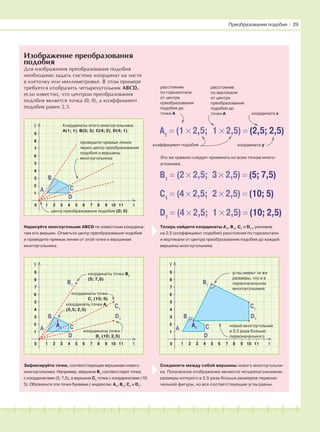
Свойства преобразования подобия
Изображение преобразования
подобия
Масштабирование
Выбор масштаба
Как произвести
масштабирование
3
4
4
6
6
6
7
7
7
8
8
9
9
9
9
10
10
10
11
11
12
12
12
13
13
14
14
15
15
16
16
17
17
18
18
18
19
19
19
20
20
21
22
22
23
23
24
24
25
25
26
26
27
28
28
29
30
30
30](https://image.slidesharecdn.com/5-200114072406/85/5-90-320.jpg)


