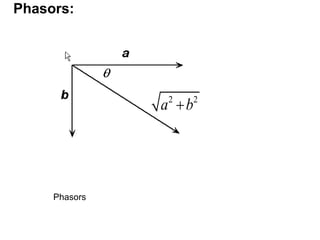
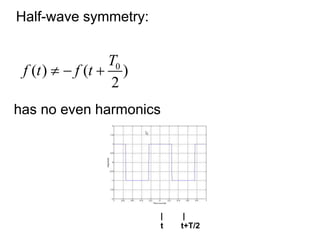
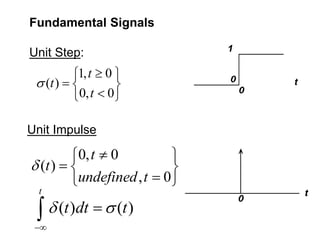
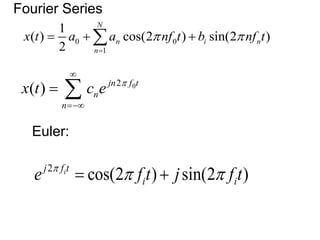This document discusses Fourier series and their properties. Fourier series can be used to represent periodic functions as the sum of sinusoids. The coefficients in the Fourier series depend on integrals of the function over one period. Fourier series are useful for analyzing signals that repeat over time.

1. Fourier Series

2. Fourier Series
2
0 0
0
2
0 0
0
1
( )cos(2 ) ( )
1
( )sin(2 ) ( )
n
n
a x t nf t d t
b x t nf t d t


 

 





0
0
0 0
0 0
0 0
1
2
1 2
( ) 2 2
f
T
t f t
d t f dt dt dt
T T
 

  


  
is the “fundamental frequency”
0 0
1
1
( ) cos(2 ) sin(2 )
2
N
n i n
n
x t a a nf t b nf t
 

  


3. Fourier Series
2
0 0
0
2
0 0
0
1
( )cos(2 ) ( )
1
( )sin(2 ) ( )
n
n
a x t nf t d t
b x t nf t d t


 

 





0
0
0 0
0 0
0 0
1
2
1 2
( ) 2 2
f
T
t f t
d t f dt dt dt
T T
 

  


  
is the “fundamental frequency”
0 0
1
1
( ) cos(2 ) sin(2 )
2
N
n i n
n
x t a a nf t b nf t
 

  


4. Fourier Series
Integration limits: when 0 2
t
 
 , then
0 0 0
2 2 1
2 /
t
T T
 
 
  
so we get:
0 0
1
1
( ) cos(2 ) sin(2 )
2
N
n i n
n
x t a a nf t b nf t
 

  

0
0
0
0 0
0
0 0
2
( )cos(2 )
2
( )sin(2 )
T
n
T
n
a x t nf t dt
T
b x t nf t dt
T







5. Fourier Series
Euler:
0 0
1
1
( ) cos(2 ) sin(2 )
2
N
n i n
n
x t a a nf t b nf t
 

  

2
cos(2 ) sin(2 )
i
j f t
i i
e f t j f t

 
 
0
2
( ) jn f t
n
n
x t c e 


 

6. Fourier Series
0
2
( ) jn f t
n
n
x t c e 


 
0
0
0
2
0
2
1
( )
T
jn t
n
T
c x t e dt
T



 
We can show
2 2
n n n
c a b
  1
tan ( / )
n n
b a
 

;
recall that
2 2 1
cos( ) sin( ) cos( tan ( ))
b
a b a b
a
   
   

7. Phasors:
Phasors
2 2
a b


8. Symmetry
Odd f(-t) =-f(t)
Fourier: sine terms
only
Even f(t) = f(-t)
Fourier: cosine terms
only
Neither

9. Half-wave symmetry:
0
( ) ( )
2
T
f t f t
  
has no even harmonics
| |
t t+T/2

10. Example of non-symmetric waveform:
0
( ) ( )
2
T
f t f t
  

11. Fundamental Signals
Unit Step:
1, 0
( )
0, 0
t
t
t


 
  

 

12. Fundamental Signals
Unit Step:
1, 0
( )
0, 0
t
t
t


 
  

 
Unit Impulse
0, 0
( )
, 0
t
t
undefined t


 
  

 
( ) ( )
t
t dt t
 


