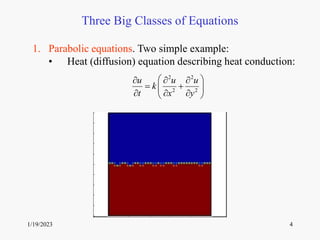
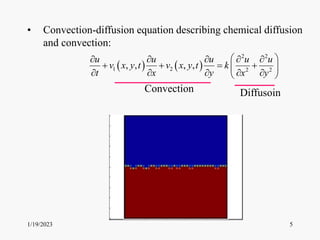
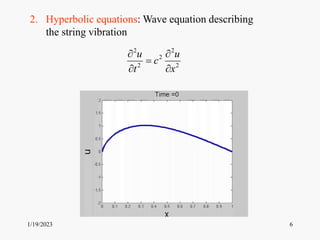
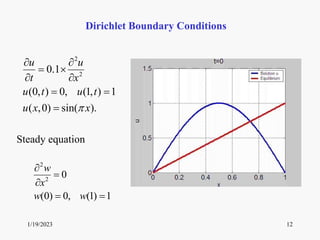
This document introduces partial differential equations (PDEs) and discusses three main classes of PDEs - parabolic, hyperbolic, and elliptic equations. It provides examples of common PDEs like the heat equation and wave equation. The document outlines the topics that will be covered in a course on PDEs, including methods for finding exact and numerical solutions to PDEs like separation of variables, Fourier series, and characteristics. It presents the tentative schedule covering derivation and solving techniques for common PDEs over several weeks.

1. Weijiu Liu
Department of Mathematics
University of Central Arkansas
Introduction to Partial Differential Equations

2. 1/19/2023 2
Overview

3. 1/19/2023 3
What are PDEs?
2 2
2 2
sin cos
u u u u u u
x y u xyt
t x y x x y
     
    
     
An equation containing an unknown function and its
partial derivatives:

4. 1/19/2023 4
Three Big Classes of Equations
2 2
2 2
u u u
k
t x y
 
  
 
 
  
 
1. Parabolic equations. Two simple example:
• Heat (diffusion) equation describing heat conduction:

5. 1/19/2023 5
   
2 2
1 2 2 2
, , , ,
u u u u u
v x y t v x y t k
t x y x y
 
    
   
 
    
 
• Convection-diffusion equation describing chemical diffusion
and convection:
Convection Diffusoin

6. 1/19/2023 6
2 2
2
2 2
u u
c
t x
 

 
2. Hyperbolic equations: Wave equation describing
the string vibration

7. 1/19/2023 7
2 2 2
2 2 2
0
u u u
x y z
  
  
  
3. Elliptic equations: Laplace’s equation

8. 1/19/2023 8
What we want to do about the equations
• Find an exact solution
• Find a numerical solution
• Study their well-posedness
• Study their stability
• Design a control law to force their solution
to your desired one
• More …

9. 1/19/2023 9
What are methods to find a solution
• Separation of variables
• Fourier series
• Fourier transformation
• Laplace transformation
• Method of characteristics
• Green functions
• D’Alembert’s formulas
• Symmetry analysis
• More …

10. 1/19/2023 10
Tentative schedule
• Derivation of the heat equation, 1 week
• Separation of variables for solving the heat
equation and Laplace’s equation, 2 weeks
• Fourier series, 3 weeks
• Derivation of the wave equation, 1 week
• Separation of variables for solving the wave
equation, 1week
• High dimensional equations, 3 weeks
• Non-homogeneous problems, 2 weeks
• Equations on infinite domains, 1 week

11. 1/19/2023 11
Equilibrium

12. 1/19/2023 12
Dirichlet Boundary Conditions
2
2
0.1
(0, ) 0, (1, ) 1
( ,0) sin( ).
u u
t x
u t u t
u x x

 
 
 
 

2
2
0
(0) 0, (1) 1
w
x
w w



 
Steady equation

13. 1/19/2023 13
Neumann Boundary Conditions
2
2
3
0.1
(0, ) 0, (1, ) 0
( ,0) .
u u
t x
u u
t t
x x
u x x
 
 
 
 
 
 

2
2
0
(0) 0, (1) 0
w
x
w w
x x



 
 
 
Steady equation