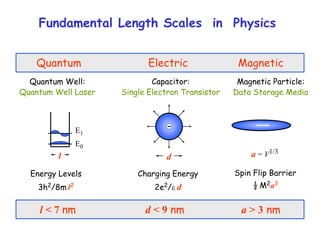
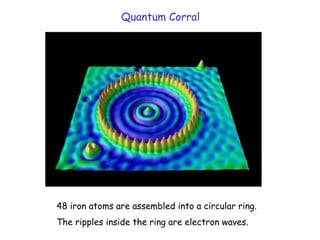
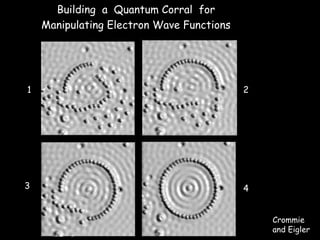
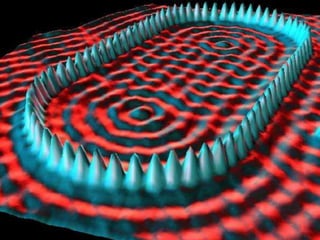
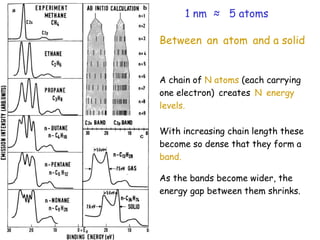
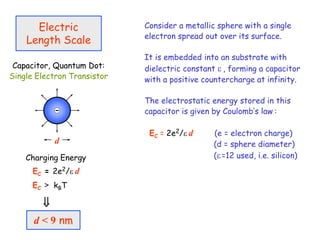
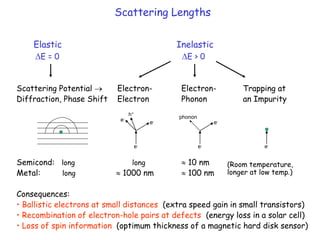
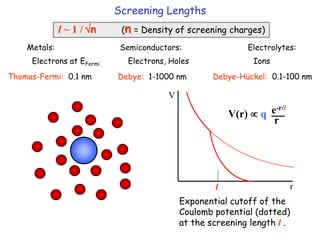
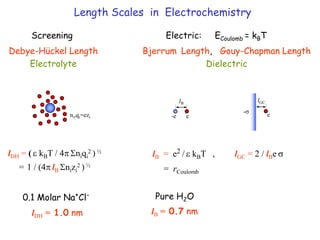
The document discusses various length scales that are important in physics, chemistry, and biology. It provides examples of fundamental length scales in quantum physics where quantum effects become prominent below 7 nanometers. In electric phenomena, the charging energy of a single electron becomes comparable to thermal energy below 9 nanometers. For magnetic structures, the energy barrier for flipping the spin of a magnetic particle must be larger than thermal energy, which requires a size above 3 nanometers. The document also discusses important length scales for polymers, electrolytes, and self-organization driven by competing short-range attraction and long-range repulsion forces between different blocks or particles.

1. Length Scales in Physics, Chemistry, Biology,…
Length scales are useful to get a quick idea what will happen when
making objects smaller and smaller. For example, quantum physics
kicks in when structures become smaller than the wavelength of
an electron in a solid. In that case, the electrons get squeezed
into a “quantum box” and have to adapt to the shape of the solid
by changing their wave function. Their wavelength gets shorter,
and that increases their energy. Since the wave function of the
outer electrons determines the chemical behavior, one is able to
come close to realizing the medieval alchemist’s dream of turning
one chemical element into another.

2. Fundamental Length Scales in Physics
Quantum Electric Magnetic
Quantum Well:
Quantum Well Laser
Capacitor:
Single Electron Transistor
Magnetic Particle:
Data Storage Media
a = V1/3
Charging Energy
2e2/ d
Spin Flip Barrier
½ M2a3
Energy Levels
3h2/8m l2
d
E1
E0
l
l < 7 nm d < 9 nm a > 3 nm

3. Quantum Corral
48 iron atoms are assembled into a circular ring.
The ripples inside the ring are electron waves.

4. Building a Quantum Corral for
Manipulating Electron Wave Functions
Crommie
and Eigler
2
1
3 4

5. http://www.almaden.ibm.com/vis/stm/gallery.html

7. Kanji character for atom
(lit. original child)
Carbon monoxide man

8. 1 nm ≈ 5 atoms
Between an atom and a solid
A chain of N atoms (each carrying
one electron) creates N energy
levels.
With increasing chain length these
become so dense that they form a
band.
As the bands become wider, the
energy gap between them shrinks.

9. Quantum
Length Scale
Quantum Well, Corral:
Quantum Well Laser
Energy Level Spacing:
E1E0 = 3h2/8m l2
E1
E0
l
l < 7 nm
Consider the two lowest energy levels of
an electron in a box (in one dimension):
The energy E of an electron is determined
by its momentum p in classical physics:
E = p2/2m (m = electron mass)
Quantum physics relates the momentum p
to the wavelength  of the electron:
p = h/ (De Broglie)
(h=Planck’s constant)
That produces an inversely quadratic
relation between E and  :
E = h2/2m 2
The quantum box restricts  :
1 = l
0 = 2 l
E1E0 > kBT


10. Electric
Length Scale
Capacitor, Quantum Dot:
Single Electron Transistor
Charging Energy
EC = 2e2/ d
d
d < 9 nm

EC > kBT
Consider a metallic sphere with a single
electron spread out over its surface.
It is embedded into an substrate with
dielectric constant  , forming a capacitor
with a positive countercharge at infinity.
The electrostatic energy stored in this
capacitor is given by Coulomb’s law :
EC = 2e2/ d (e = electron charge)
(d = sphere diameter)
(=12 used, i.e. silicon)

11. Magnetic
Length Scale
Magnetic Particle:
Data Storage Media
a = V1/3
Spin Flip Barrier
EM = ½ M2a3
a > 3 nm

EM > kBT
Consider a needle-shaped magnetic particle
with two possible magnetization directions:
The magnetic energy barrier is proportional
to the volume of the particle, i.e. the third
power of its average dimension a :
EM = ½ M2a3 (e = electron charge)
(a = average diameter)
(cgs unit system)
The magnetization M is estimated from the
magnetic moment 2B = eh/2mc of an iron
atom in a magnet and the iron atom density.

12. Elastic Inelastic
E = 0 E > 0
Scattering Potential  Electron- Electron- Trapping at
Diffraction, Phase Shift Electron Phonon an Impurity
Semicond: long long  10 nm
Metal: long  1000 nm  100 nm
Consequences:
• Ballistic electrons at small distances (extra speed gain in small transistors)
• Recombination of electron-hole pairs at defects (energy loss in a solar cell)
• Loss of spin information (optimum thickness of a magnetic hard disk sensor)
e-
e-
e-
h+
e- e-
e-
phonon
(Room temperature,
longer at low temp.)
Scattering Lengths

13. Screening Lengths
l ~ 1 / n (n = Density of screening charges)
Metals: Semiconductors: Electrolytes:
Electrons at EFermi Electrons, Holes Ions
Thomas-Fermi: 0.1 nm Debye: 1-1000 nm Debye-Hückel: 0.1-100 nm
Exponential cutoff of the
Coulomb potential (dotted)
at the screening length l .
V(r)  q e-r/l
r
V
r
l

14. Length Scales in Electrochemistry
Screening Electric: ECoulomb = kBT
Debye-Hückel Length
Electrolyte
Bjerrum Length, Gouy-Chapman Length
Dielectric
Pure H2O
lB = 0.7 nm
lB = e2 /  kBT , lGC = 2 / lBe 
= rCoulomb
lDH = (  kBT / 4 niqi
2 ) ½
= 1 / (4 lB nizi
2 ) ½
0.1 Molar Na+Cl-
lDH = 1.0 nm
ni,qi=ezi
lGC
-
e
lB
-e e

15. Length Scales in Polymers
(including Biopolymers, such as DNA and Proteins)
Random Walk, Entropy Stiffness  vs. kBT
Persistence Length
(straight segment)
lP =  / kBT
DNA (double) Polystyrene
lP  50 nm lP  1 nm
lP
cos = 1/e
a
Radius of Gyration
(overall size, N straight segments)
RG  lP N
Copolymers
RG  20-50 nm
RG

16. Self-Organization via two Competing Length Scales
Short Range Attraction versus Long Range Repulsion
Ferromagnetic Exchange: 
Magnetic Dipole Interaction: 
Ferromagnet Diblock Copolymer
Hydrophilic versus Hydrophobic
Depends on the relative block size