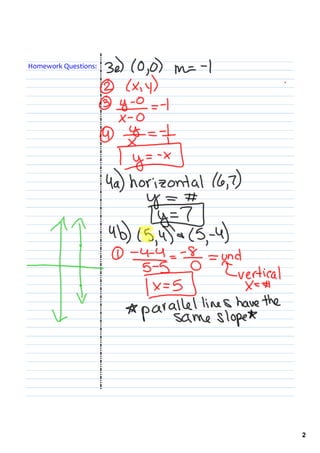
This document provides instruction on writing and graphing linear equations in different forms. It begins with a review of equivalent forms of linear equations, including point-slope, slope-intercept, and standard form. Students are then given examples of writing equations of lines given a point and slope, or two points. The document concludes with examples of graphing lines by using the point-slope and slope-intercept forms to easily find points and draw the line. Students are challenged to graph a line given in standard form and explain their process.

1. Day 2: Opener
Think back:
Complete the
following problem on a
math raffle ticket.
Good Luck!
1. Write the equation of the line that is parallel to x = ‐6 and
passes through the point (3,10).
1

2. Homework Questions:
2

3. 3

4. 4

5. Section 4.7 Jiffy Graphs
TOPIC ONE (cont.) Solve your given equation for y.
Information from
Equations
Think back: Are these equations equivalent? How do you
know?
Since they are equivalent then they should all be the
same line! This means they should all have the same
__________, ________________, and ___________.
It's Your Turn!
Complete the following 1. What is the slope of line l ?
4 questions with your
partner.(5 minutes)
2. Where does l cross the y‐axis?
3. Where does l cross the x‐axis?
4. Which equation for l makes it easiest to see that the point
(5,3) is on the line? Explain.
5

6. Linear Equation Forms Point‐Slope Form (IYT # 1 & 4):
•
•
Slope‐Intercept Form (IYT # 1 & 2):
•
•
Standard Form (IYT # 3):
•
•
6

7. TOPIC TWO We can use the different forms of linear equations that we
Writing equations of learned today to write the equation of a line in a jiffy!
lines using the
different forms.
Given slope and through (10, ‐3) with slope 7
the given point: (Ex. #1)
Step 1: Substitute the given information into point‐slope form.
Step 2: Simplify to slope‐intercept form (solve for y).
Given 2 points: (Ex. # 2) (0,7) and (‐4,9)
Step 1: Find the slope between these 2 points.
Step 2: Substitute one of the points and the slope into point‐
slope form.
Step 3: Simplify to slope‐intercept form (solve for y).
7

8. TOPIC THREE Think back: How did we graph equations last chapter?
Jiffy Graphing
We are going to use the forms of linear equations to help us
graph in a jiffy!
Using Point‐Slope Graph y+2 = ‐3(x+1).
Form: (Ex. # 3)
Step 1: Plot the given point.
Step 2: Use the slope to
plot two more points.
Step 3: Connect all three
points with a line.
Using Slope‐Intercept Graph y = 1.75x ‐1.
Form: (Ex.#4)
Step 1: Plot your
y‐intercept.
Step 2: Use the slope to
plot two more points.
Step 3: Connect all three
points with a line.
8

9. Exit Slip: 1.) Think about how you might graph the equation of a line
given to you in standard form. Write down what your method
would be on a half‐sheet of paper and turn it in before you
leave.
Think back:
What information can
you easily get from
standard form?
OR
Can you change it to an
equivalent form?
2.) Graph 3x+4y = 12 using your method.
9

10. 10