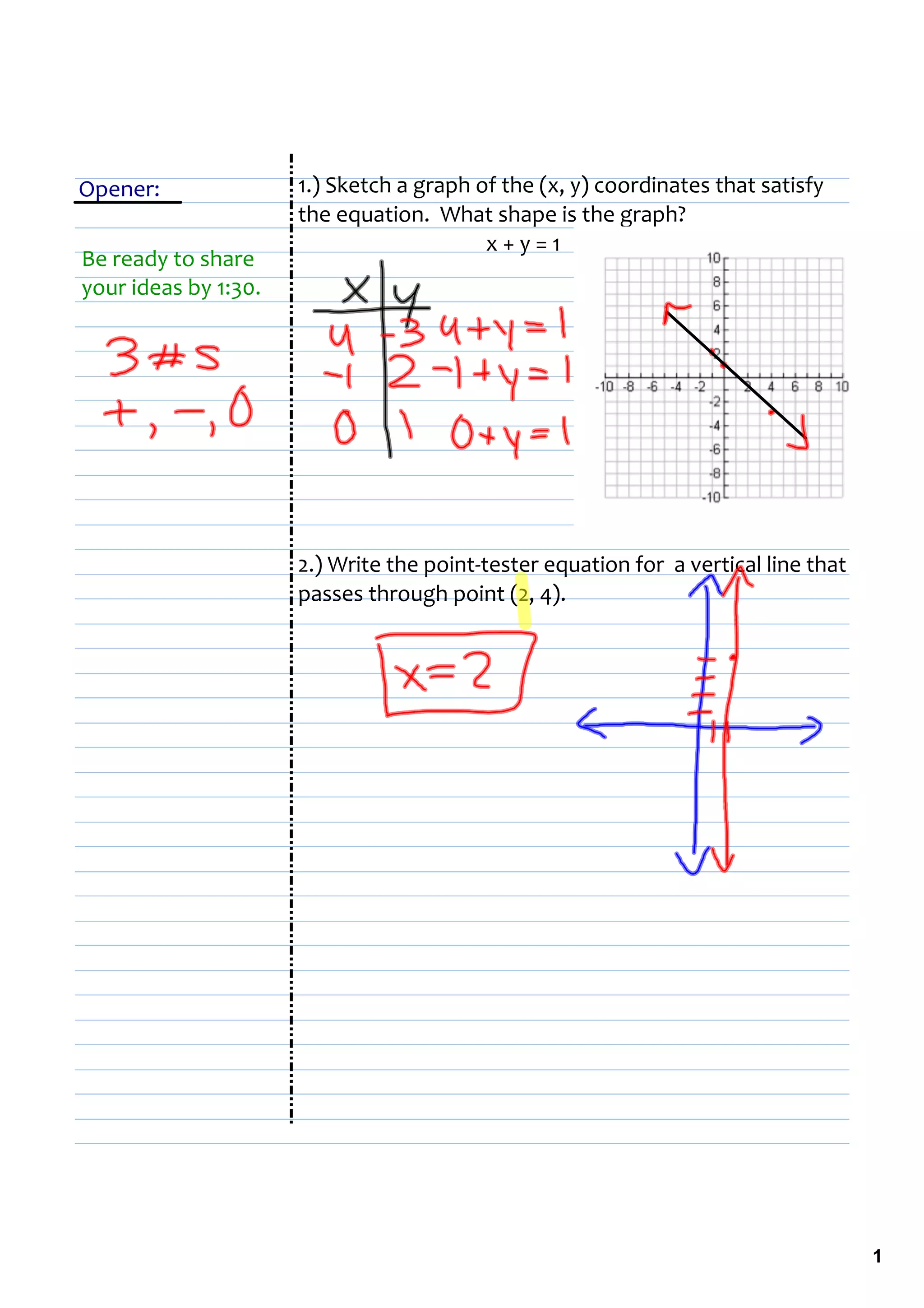
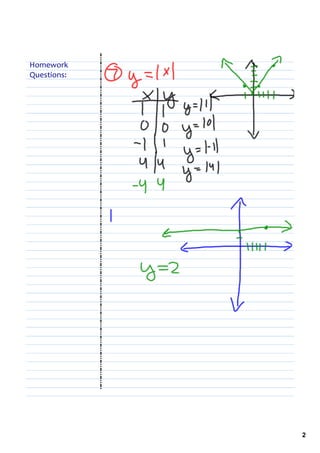
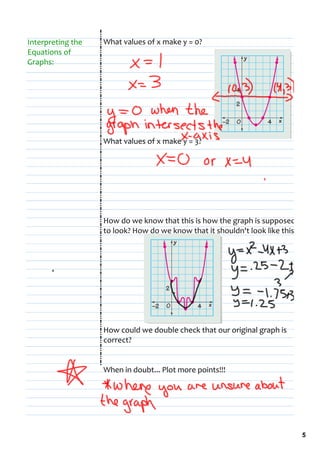
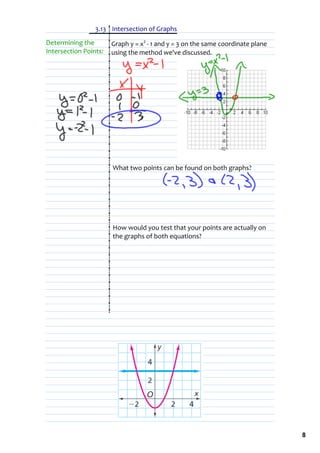
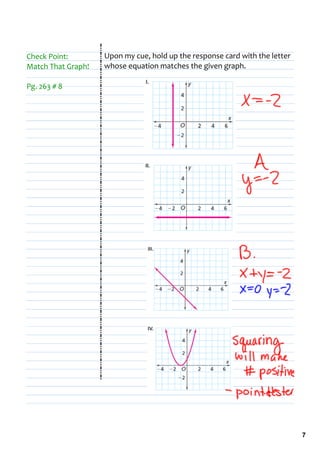
1) The document discusses graphing equations and finding intersection points of graphs. It includes examples of graphing equations like y = x2 - 4x + 3 and finding the intersection points of the graphs y = x and y = 1000 - x. 2) Tony and Sasha's method for graphing y = x2 - 4x + 3 involved choosing x-values of 0 and -1 to plot points and draw a curve between them. 3) The document provides homework problems from pages 263 and 267 involving graphing equations and finding intersection points.

1. Opener: 1.) Sketch a graph of the (x, y) coordinates that satisfy
the equation. What shape is the graph?
x + y = 1
Be ready to share
your ideas by 1:30.
2.) Write the point‐tester equation for a vertical line that
passes through point (2, 4).
1

2. Homework
Questions:
2

3. 12/9 & 12/10: 3.12 Graphing by Plotting
Launch: How do you graph the equation y = x2 ‐ 4x + 3?
Open your books to Tony:
page 258. Sasha:
Narrator:
Everyone else: Follow along carefully and be prepared
to answer questions about the reading.
3

4. Minds in Action: 1.) How is this equation different from 2x + 3y = 12,
which we worked with last class?
2.)Briefly summarize Tony and Sasha's method so far.
3.) Why did they choose the x values of 0 and ‐1?
4.) Do we have enough points to draw a line to
complete the graph?
5.) Write down a brief summary of the reading. Be
sure to include at least two key ideas that you want to
remember.
4

5. Interpreting the What values of x make y = 0?
Equations of
Graphs:
What values of x make y = 3?
How do we know that this is how the graph is supposed
to look? How do we know that it shouldn't look like this?
How could we double check that our original graph is
correct?
When in doubt... Plot more points!!!
5

6. Ms. Betzel says.... • One partner from every partnership should take out
a sheet of paper.
• Imagine your piece of paper is a coordinate plane.
• In big letters, write A in the 1st quadrant, B in the 2nd,
C in the 3rd, and D in the 4th.
• Crease and tear the paper along the x‐axis.
• Give your partner the 3rd and 4th quadrants.
• Crease and tear the paper along the y‐axis.
6

7. Check Point: Upon my cue, hold up the response card with the letter
Match That Graph! whose equation matches the given graph.
Pg. 263 # 8
7

8. 3.13 Intersection of Graphs
Determining the Graph y = x2 ‐ 1 and y = 3 on the same coordinate plane
Intersection Points: using the method we've discussed.
What two points can be found on both graphs?
How would you test that your points are actually on
the graphs of both equations?
8

9. Intersection Points: The points where two graphs cross are intersection
points.
• An intersection point of two graphs satisfies _______
of the corresponding equations.
• If a point makes two equations true, then it is an
______________ _______ of the corresponding
graphs.
9

10. Challenge Problem: Earlier we graphed the equation y = x2 ‐ 4x + 3, which
Tony said looked like a big smile.
Give an equation with a graph that has the shape of a
big frown.
(*Hint: Recall our discussion with transformations).
10

11. Exit Slip: The graphs of y = x and y = 1000 ‐ x intersect at one
point. Explain why each point is not the intersection of
Please turn in the two graphs.
worksheet before
you leave. a. (100, 25)
b. ( ‐ 25, ‐ 25)
11

12. Homework: Pg. 263 # 4, 7, 9‐ 10 & 12‐13
Pg. 267 # 6‐ 10
12

13. 13

14. 14

15. 15

16. 16

17. 17

18. 18

19. 19