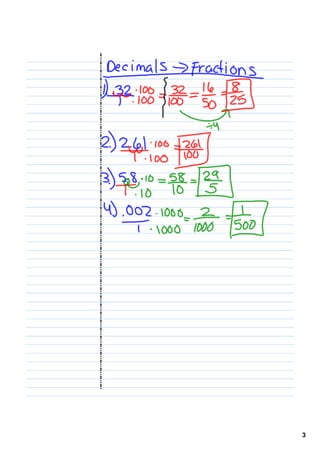
This document contains notes and instructions for a math lesson that includes: 1) Solving expressions and evaluating them for given values. 2) Completing an in-class activity with partners to review basic arithmetic rules. 3) Practicing the basic rules of arithmetic through examples of simplifying expressions using properties like commutative, associative, and distributive properties.

1. *Remember to write down any homework questions that
Opener: you had on the backboard BEFORE doing the opener!
1. A rectangle has length 12x ‐ 7 and width 5. Find an
expression for the area and an expression for the perimeter.
2. Evaluate the expression 5(2x ‐ 7) ‐ 3(3x ‐ 10) for each
of the following values.
a. 4 b. ‐5 c. d. 0
1

2. Quiz Time!!! When you have finished the quiz, pick up Weekly Review # 2
from me, and you can get started on it SILENTLY!
2

3. 3

4. Section 2.5 Rephrasing the Basic Rules
Partner Basic Rules Open your books to page 110. Complete the In‐Class
Activity Experiment with your partners in your notes. Each of you
must write down the letter from List 2 next to the number it
corresponds to in List 1. You DO NOT need to write out each
statement in full.
When you are done, read through the Facts and Notation on
page 111 quietly.
4

5. The Basic Rules of Commutative Property of Addition:
Arithmetic
Associative Property of Addition:
Commutative Property of Multiplication:
Associative Property of Multiplication:
Distributive Property:
Additive Identity:
Multiplicative Identity:
Additive Inverse:
Multiplicative Inverse:
5

6. Practicing the Basic Ex 1: Express each sentence without using variables:
Rules of Arithmetic
a. Dividing is the same as multiplying by the reciprocal.
b. Subtracting is the same as adding the opposite.
c. If you have a product of two numbers, and you find the
products of the opposites of the numbers, you get the same
result.
d. If you multiply two numbers together and the result is 1, the
numbers are reciprocals.
Ex 2: Find each product. Look for patterns.
a.
b.
c.
d. Describe a pattern.
6

7. Expressions Survivor!!! Complete each of the following problems in your notes. Once
you agree on a final response write it down on your board,
and lay your board face down until I say BOARDS UP! Be
careful in your work, as any incorrect answer will get you
eliminated from the game.
Use the Commutative & Associative Properties and the
Distributive Property to simplify each expression. Please
write down which properties you used in simplifying each one.
a. 2(x + 4) + 7
b. 13 + 3(1 + 2x)
c. 3(2x ‐ 5) ‐ 8
d. 4(x + 3) + 7(x + 3)
e. 6(3 ‐ 2x) ‐ 3(x + 1)
7

8. 8