The document provides information about direct and inverse variation, including: 1) Examples of direct variation relationships involving weeks in a year, minutes in an hour, and feet in an inch. Equations are given to represent these relationships. 2) Examples are worked through using the direct variation equations to find requested values involving hours in days and inches in a cabinet. 3) Key properties of direct variation are described, such as what happens when one quantity doubles or decreases while the other stays the same. 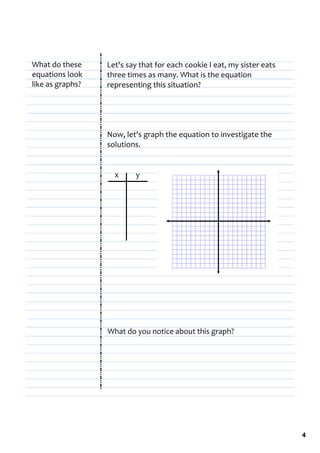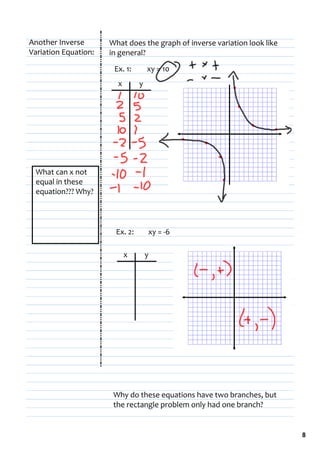4) An example of an inverse variation relationship involving the area of a rectangle and length/width is given, and the graph of this relationship is discussed.

1. Launch: Please find the errors in the problems on the half sheet of paper.
1

2. Section 3.15: Two basic graphs: y = cx & y = c
x
y = cx Describes the relationship between things that are in
a constant ratio.
( ) Ex. 1: The days in each week.
Ex. 2: The weeks in each year.
Ex. 3: The minutes in each hour.
Your turn:
1. Write a direct variation equation to represent
the number of hours in a day.
2. Write a direct variation equation to represent
the number of feet in an inch.
2

3. Using these Use the information and the corresponding equation
equations: to find the requested value.
1. If 120 hours have past since your birthday, how
many days is that?
2. If a cabinet in your house is 4 feet 6 inches tall,
how many inches is that?
3. If you have been working at your job for 37
weeks, how many years is that?
Thinking about When your situation is modeled by direct variation,
what these if:
equations mean:
1. One quantity doubles, then:
2. One quantity decreases, then:
3. One quantity stays the same, then:
3

4. What do these Let's say that for each cookie I eat, my sister eats
equations look three times as many. What is the equation
like as graphs? representing this situation?
Now, let's graph the equation to investigate the
solutions.
x y
What do you notice about this graph?
4

5. Your Turn: Each time a student babysits, they make $30.
Write a direct variation equation and graph it.
x y
5

6. y = c Describes the relationship between things that have
a constant product.
x Ex. 1: Suppose you have $100 to divide equally
( ) among your friends.
What are some ways you could do this?
Ex. 2: A rectangle has an area of 80 in2.
What are the possibilities for the length
and width?
6

7. Let's look at the Some of the values we came up with for length
rectangle and width are:
example from
before.
Let's graph these and see what happens...
What about the places between these points?
Would these in between points also make the
rectangle's area 800?
Is there an equation for this graph?
7

8. Another Inverse What does the graph of inverse variation look like
Variation Equation: in general?
Ex. 1: xy = 10
x y
What can x not
equal in these
equation??? Why?
Ex. 2: xy = ‐6
x y
Why do these equations have two branches, but
the rectangle problem only had one branch?
8

9. Homework: p. 281 #1, 2, 3abc, 4abc, 5, 7bc, 10, 12, 14
9

10. 10