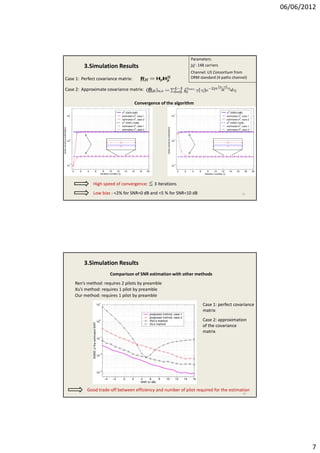
1. An iterative algorithm is proposed for jointly estimating SNR and the frequency selective channel for OFDM systems. 2. The algorithm estimates the channel using LMMSE estimation and estimates the noise variance using MMSE estimation at each iteration. SNR is then derived from the noise variance estimate. 3. Simulation results show the algorithm converges quickly within 3 iterations with low estimation bias for SNR and channel. SNR estimation accuracy is better than other methods using fewer pilots.

1. 06/06/2012
1
SEMINAIRE SCEE
26 avril 2012
Supélec, campus de Rennes
Présentation : Vincent Savaux
April 17‐20, 2012
Poznań, Poland
An Iterative and Joint Estimation of SNR andAn Iterative and Joint Estimation of SNR and
Frequency Selective Channel for OFDM Systems
Authors :
Vincent Savaux , Yves Louët , Moïse Djoko‐Kouam and Alexandre Skrzypczak
Speaker: Vincent Savaux, PhD student
1,2 1 12
ECAM Rennes – Louis de Broglie, Rennes Campus, France
1 SUPELEC, Rennes Campus , France2

2. 06/06/2012
2
An Iterative and Joint Estimation of SNR and
Frequency Selective Channel for OFDM Systems
1. Background
 System Model
 Estimation Methods
2. Proposed Method
 Presentation of the Algorithm
 Convergence of the Algorithm
3
3. Simulation Results
4. Conclusion
1.Background
System Model
In the frequency domain, the received OFDM symbol is:
DFT size =
0
0
+
Matrix of the emitted
OFDM symbol
Frequency
channel response
AWGNVector of the received
OFDM symbol
4
with
: zero mean Gaussian process
: number of paths of the channel
: path delay
,

3. 06/06/2012
3
1.Background
Estimation Methods ‐ Signal to noise ratio (SNR, noted )
, with the second moment‐order of the received signal
[1]: estimated thanks to the subtraction of two consecutive received
signal vectors
[2]: estimated thanks to the subspace properties of the estimated
covariance matrix of the received signal
5
G. Ren, H. Zhang, and Y. Chang, “SNR Estimation Algorithm Based on the Preamble for OFDM Systems in Frequency Selective
Channels,” IEEE Transactions on Communications, vol. 57, no. 8, August 2009.
X. Xu, Y. Jing, and X. Yu, “Subspace‐Based Noise Variance and SNR Estimation for OFDM Systems,” in IEEE Mobile Radio
Applications Wireless Communication Networking Conference, March 2005, pp. 23 –26.
[1]
[2]
Our solution: estimated thanks to the MMSE criterion
1.Background
Estimation Methods ‐ Noise estimation
MMSE criterion performed on the pilot (index )
‐=
22
6
In practice: approximation of MMSE criterion
The noise variance estimation depends on the channel estimation quality

4. 06/06/2012
4
1.Background
Estimation Methods ‐ Channel estimation
Least square (LS) estimator:
Linear minimum mean square error (LMMSE) estimator:
,
with the frequency covariance matrix of the channel
For the noise variance estimation:
7
LS estimator: not adapted for the noise variance estimation
leads to
LMMSE estimator: efficient estimator, adapted for the noise variance estimation
requires nevertheless an estimation of the noise variance
2.Proposed Method
Presentation of the Algorithm
We suppose pilots as
requiresProblem: , and requires
Solution an iterative algorithm
LMMSE
channel
estimation
Solution: an iterative algorithm
MMSE noise
variance
estimation
SNR
estimation
At each iteration , we do
8
,

5. 06/06/2012
5
2.Proposed Method
Presentation of the Algorithm
LMMSE
h l
MMSE noise
variance
estimation
SNR
estimation
Initialization of the Algorithm:
If , the LMMSE estimation is equivalent to the LS one:
channel
estimation
9
The initialization is chosen so that
2.Proposed Method
Convergence of the Algorithm ‐ noise variance
From the theoretical expression of the MMSE noise variance estimation:
eigenvalues of
C b l i ith
After some mathematical developments:
One example of f(x)
10
Convergence by solving with
Solution: the fixed point theorem

6. 06/06/2012
6
2.Proposed Method
Convergence of the Algorithm
Solution: the fixed point theorem applied to the function
One example of f(x)
is upper and lower bounded:
, so is strictly growing
has at least one fixed point
with the number of paths of the channel
11
is monotonous
converges to a fixed point of
p
Unicity of convergence soon published
2.Proposed Method
Convergence of the Algorithm ‐ channel estimation
Thanks to
Noise variance estimation
converges converges
Estimated values
12
Channel estimation
What about the speed of convergence and the bias of the estimator ?
Real values

7. 06/06/2012
7
3.Simulation Results
Perfect covariance matrix:
Approximate covariance matrix:
Case 1:
Case 2:
Convergence of the algorithm
Parameters:
: 148 carriers
Channel: US Consortium from
DRM standard (4 paths channel)
Convergence of the algorithm
13
High speed of convergence: 3 iterations
Low bias : <2% for SNR=0 dB and <5 % for SNR=10 dB
3.Simulation Results
Comparison of SNR estimation with other methods
Ren’s method: requires 2 pilots by preamble
Xu’s method: requires 1 pilot by preamble
Our method: requires 1 pilot by preamble
Case 1: perfect covariance
matrix
Case 2: approximation
of the covariance
matrix
14
Good trade‐off between efficiency and number of pilot required for the estimation

8. 06/06/2012
8
3.Simulation Results
Channel estimation
15
Proof by simulation of the convergence of the channel estimation
Gap between perfect estimation and Case 2 <0.5 dB (<0.1 dB in Case 1)
4.Conclusion
• New algorithm for joint estimation of SNR and multipath channel
• Proof of convergence of the algorithm
• Good quality of channel and SNR estimations with high speed of convergence
• Improvement of the trade‐off between the number of required pilots and quality of
estimation, compared with existing methods in literature
• Further works and publications :
‐Unicity of convergence of the algorithm
16
‐Development of a practical solution with an estimated frequency channel
covariance matrix

9. 06/06/2012
9
Thank you for your attention
Questions ? …
17