Recommended
PDF
PDF
PDF
資料】<福島第一原子力発電所事故により放出されたヨウ素131の地表面沈着量を導出>
PDF
BGI Webinar June 6, 2014 "Genomic Big Data Analysis and Customised Analysis w...
PDF
中央大学学術講演会(2013年6月15日)ゲノム科学でわかること
PPTX
近大「基礎生物学」#8「細胞内の遺伝情報」130610
PPTX
OR学会 2015/9/11 組合せ最適化の体系化とフリーソフトによる最適化
PDF
コンピュータービジョン最先端ガイド2 3.4ベクトルデータに対するカーネル法(SVM)
PDF
第3回NGS現場の会モーニング教育セッション 配布用資料
PDF
NGS現場の会 第3回 モーニング教育セッション 配布用資料 「いまさら聞けない NGS超!入門」
PDF
PDF
非線形データの次元圧縮 150905 WACODE 2nd
PDF
PPTX
PPTX
PPTX
組合せ最適化を体系的に知ってPythonで実行してみよう PyCon 2015
PDF
PDF
PDF
PDF
PDF
2015年度先端GPGPUシミュレーション工学特論 第13回 数値流体力学への応用�(高度な最適化)
PDF
20181212 - PGconf.ASIA - LT
PDF
非静力学海洋モデルkinacoのGPUによる高速化
PDF
CMSI計算科学技術特論A (2015) 第11回 行列計算における高速アルゴリズム2
PDF
GPU-FPGA 協調計算を記述するためのプログラミング環境に関する研究(HPC169 No.10)
PDF
GPGPU Education at Nagaoka University of Technology: A Trial Run
PDF
PDF
アニメーション(のためのパフォーマンス)の基礎知識
PDF
AngularJSでデータビジュアライゼーションがしたい
PDF
GDG DevFest Kobe Firebaseハンズオン勉強会
More Related Content
PDF
PDF
PDF
資料】<福島第一原子力発電所事故により放出されたヨウ素131の地表面沈着量を導出>
PDF
BGI Webinar June 6, 2014 "Genomic Big Data Analysis and Customised Analysis w...
PDF
中央大学学術講演会(2013年6月15日)ゲノム科学でわかること
PPTX
近大「基礎生物学」#8「細胞内の遺伝情報」130610
PPTX
OR学会 2015/9/11 組合せ最適化の体系化とフリーソフトによる最適化
PDF
コンピュータービジョン最先端ガイド2 3.4ベクトルデータに対するカーネル法(SVM)
Viewers also liked
PDF
第3回NGS現場の会モーニング教育セッション 配布用資料
PDF
NGS現場の会 第3回 モーニング教育セッション 配布用資料 「いまさら聞けない NGS超!入門」
PDF
PDF
非線形データの次元圧縮 150905 WACODE 2nd
PDF
PPTX
PPTX
PPTX
組合せ最適化を体系的に知ってPythonで実行してみよう PyCon 2015
PDF
PDF
PDF
Similar to 201010ksmap
PDF
PDF
2015年度先端GPGPUシミュレーション工学特論 第13回 数値流体力学への応用�(高度な最適化)
PDF
20181212 - PGconf.ASIA - LT
PDF
非静力学海洋モデルkinacoのGPUによる高速化
PDF
CMSI計算科学技術特論A (2015) 第11回 行列計算における高速アルゴリズム2
PDF
GPU-FPGA 協調計算を記述するためのプログラミング環境に関する研究(HPC169 No.10)
PDF
GPGPU Education at Nagaoka University of Technology: A Trial Run
More from Yosuke Onoue
PDF
PDF
アニメーション(のためのパフォーマンス)の基礎知識
PDF
AngularJSでデータビジュアライゼーションがしたい
PDF
GDG DevFest Kobe Firebaseハンズオン勉強会
PDF
PDF
asm.jsとWebAssemblyって実際なんなの?
PDF
PDF
AngularJSとD3.jsによるインタラクティブデータビジュアライゼーション
PDF
PDF
PDF
PDF
Anaconda & NumbaPro 使ってみた
PDF
KEY
What's New In Python 3.3をざっと眺める
KEY
PyOpenCLによるGPGPU入門 Tokyo.SciPy#4 編
KEY
PPTX
PPT
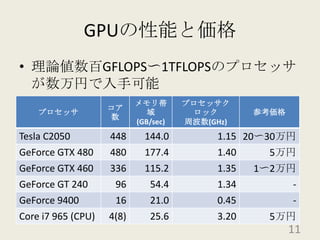
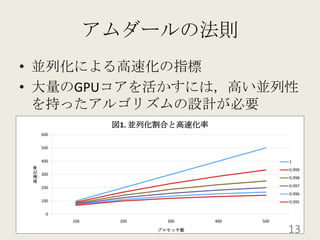
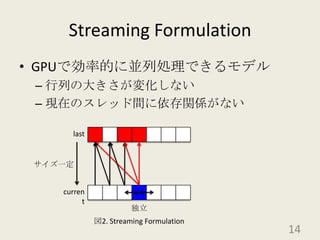
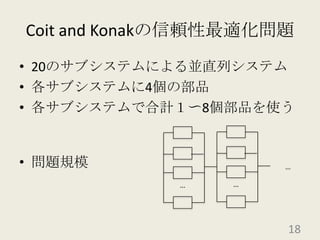
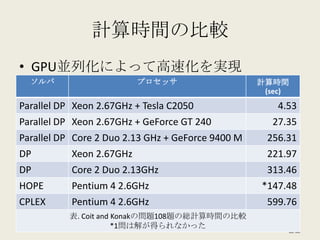
201010ksmap 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. Coit and Konakの信頼性最適化問題D.W. Coit, A. Konak「Multiple weighted objectives heuristic for the redundancy allocation problem」IEEE Trans. Reliab., 55(3), pp.551-558, 2006.部品間のトレードオフを考慮して作成されている17 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29.