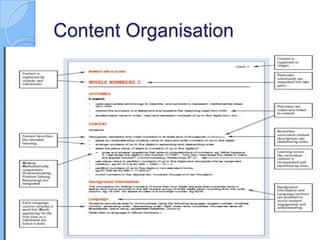
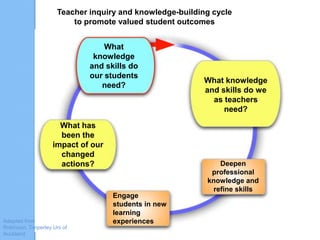
This document summarizes a session for guiding school leaders on the NSW syllabus for the Australian curriculum: Mathematics K-10. It explores the structure of the new syllabus, focusing on elements like the aim, objectives, stage statements, and content organization. It discusses comparing the current and new syllabuses for Early Stage 1, Stage 1, and Stage 2. It also includes activities for teachers to analyze content from these stages. The document emphasizes understanding the implications of changes between syllabuses for teaching practice and professional learning.

1. NSW SYLLABUS for the
Australian curriculum
Mathematics K-10 (Vol. 1)
Guiding school leaders
Diocese of Broken Bay

2. Session One:
Learning Intent:
To explore the structure of the new syllabus
(2014), focusing on:
 Aim
 Objectives
 Stage statements
 Strand overviews
 Content organisation
 Coding and Icons
 Outcome statements
 Pedagogical implications

3. Aim (p. 16):
The aim of Mathematics in K–10 is for students to:
• be confident, creative users and communicators of
mathematics, able to investigate, represent and interpret
situations in their personal and work lives and as active
citizens
• develop an increasingly sophisticated understanding of
mathematical concepts and fluency with mathematical
processes, and be able to pose and solve problems and
reason in Number and Algebra, Measurement and
Geometry, and Statistics and Probability
• recognise connections between the areas of
mathematics and other disciplines and appreciate
mathematics as an important aspect of lifelong learning.

4. Reflecting on the aim
 In what ways does teaching and
learning in your school currently enact
these aims?
 What challenges do the aims pose for
you, given your knowledge of how
mathematics is currently taught and
learned at your school?

5. Objectives (p. 16):
 KNOWLEDGE, SKILLS AND UNDERSTANDING Students:
Working Mathematically
• develop understanding and fluency in mathematics through inquiry, exploring and
connecting mathematical concepts, choosing and applying problem-solving skills and
mathematical techniques, communication and reasoning
Number and Algebra
• develop efficient strategies for numerical calculation, recognise patterns, describe
relationships and apply algebraic techniques and generalisation
Measurement and Geometry
• identify, visualise and quantify measures and the attributes of shapes and objects, and
explore measurement concepts and geometric relationships, applying formulas, strategies
and geometric reasoning in the solution of problems
Statistics and Probability
• collect, represent, analyse, interpret and evaluate data, assign and use
probabilities, and
make sound judgements.

6. Objectives
 VALUES AND ATTITUDES
Students:
• appreciate mathematics as an essential and relevant part
of life, recognising that its cross-cultural development has
been largely in response to human needs
• demonstrate interest, enjoyment and confidence in the
pursuit and application of mathematical knowledge, skills
and understanding to solve everyday problems
• develop and demonstrate perseverance in undertaking
mathematical challenges.
How can we foster these dispositions?

7. Stage Statements (p. 26)
 Foundation
statements have
been replaced by
stage statements
which reflect the
intent of the
Australian
Curriculum
Achievement
Standards.
 Stage statements
summarise the
knowledge, understa
nding, skills, values
and attitudes that
students develop as

8. Organisation of content (p.
32)

9. Strand Overviews (p. 33)
Working Mathematically
- Give an example of a time you have seen a child
problem solve, communicate mathematically or reason.
Share an example of a lesson where students were not
given opportunities to work mathematically.
Number and Algebra
- Identify some ways Number and Algebra are
fundamental to the other strands. What are the
implications of this?
Measurement and Geometry
- Read the strand overview. How are measurement and
geometry interrelated?
Statistics and Probability
- Why is Statistics and Probability an important aspect of
the syllabus?

10. Content Organisation

11. Coding and Icons: (p. 12)

12. What are the pedagogical
implications? Pg. 17

13. Session 2:
Learning Intent:
 To highlight the differences between the
current and new syllabuses and explore
the implications for teaching.
Focusing on:
• Early Stage 1
• Stage 1
• Stage 2

14. Early Stage 1
1. Select a Strand
2. Compare the current syllabus to the
new syllabus
- What is the same?
- What is different?
- What do you notice?
- What are the implications for PL?
3. Share in table groups

15. Stage 1
1. Select a Strand
2. Compare the current syllabus to the
new syllabus
- What is the same?
- What is different?
- What do you notice?
- What are the implications for PL?
3. Share in table groups

16. Activity: Using ES1/ Stage 1
Content
 Choose a number between 20 and
300.
 Partition it using place value as many
different ways as you can.
 Can you position your number on an
empty number line?

17. Discussion:
 What is the syllabus outcome?
 What is the content knowledge
teachers need to know to teach this?
 Why is it important for students to be
able to partition?
 Where does this fit in on the
continuum of learning?

18. Language
The bold words are terms that are
being introduced for the first time.

19. Stage 2
1. Select a Strand
2. Compare the current syllabus to the
new syllabus
- What is the same?
- What is different?
- What do you notice?
- What are the implications for PL?
3. Share in table groups

20. Activity: Stage 2
The new syllabus has a much stronger focus on
quadrilaterals.
Take a look at Two- Dimensional Space 1 and 2
(Stage 2) in particular the language section.
1. Draw two non- congruent quadrilaterals on 3 x 3
dots.
2. Record the properties of your shape. Can you
use the language from the syllabus?
3. As a group agree on a rule for classification
4. Does your criteria make sorting easy?
5. Can you make another so all items can be
sorted?

21. Discussion:
 What is the syllabus outcome?
 What is the content knowledge
teachers need to know?
 What will it look like when this content
is taught for conceptual
understanding?
 How will you ensure this is taught
conceptually and not procedurally?
 Where does this fit in on the
continuum of learning?

22. Session 3:
Learning Intent:
 To highlight the differences between
the current and new syllabuses and
explore the implications for teaching.
Focusing on:
Stage 3

23. Stage 3
1. Select a Strand
2. Compare the current syllabus to the
new syllabus
- What is the same?
- What is different?
- What do you notice?
- What are the implications for PL?
3. Share in table groups

24. Activity: Multiplication and Division
1. Write a multiplication sentence that is 2 digit
x 2 digit (eg: 36 x 48).
2. Using the area model to divide the grid into
sections and label the multiplication needed
for each section.
3. Are there other ways to section your array to
make calculating easier?

25. Discussion:
 What is the syllabus outcome?
 What is the content knowledge
teachers need to know?
 Why is the area model an important
representation?
 How will you ensure this is taught
conceptually and not procedurally?
 Where does this fit in on the
continuum of learning?

26. Programming

27. What
knowledge
and skills do
our students
need?
What knowledge
and skills do we
as teachers
need?
What has
been the
impact of our
changed
actions? Deepen
professional
knowledge and
refine skills
Engage
students in new
learning
experiences
Teacher inquiry and knowledge-building cycle
to promote valued student outcomes
Adapted from
Robinson, Timperley Uni of
Auckland

28. Mathematics Block Guidelines