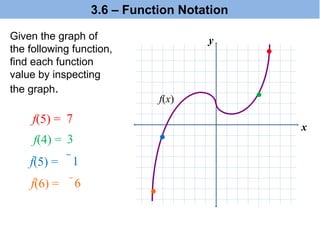
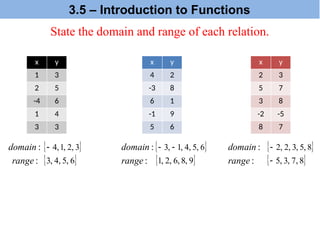
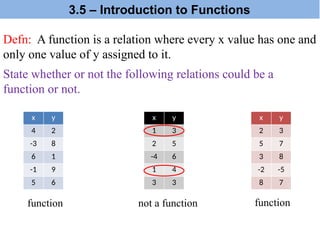
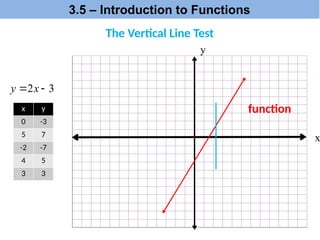
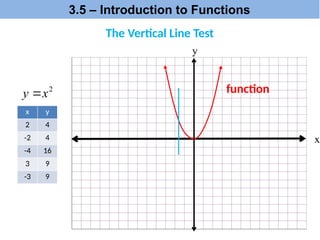
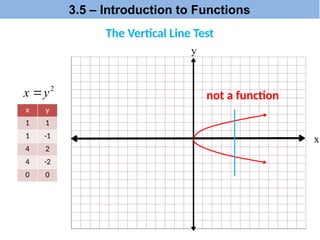
The document explains the concepts of dependent and independent variables, domain, and range in functions through examples. It provides definitions and scenarios illustrating how variables interact and emphasizes the importance of understanding functions as relations where each input corresponds to a single output. Additionally, it discusses practical applications of these concepts, including function notation and the vertical line test for determining functions.

1. Determining the
Dependent and
Independent Variables
and Finding the
Domain and Range of a
Function

2. ACTIVITY 1: THE VARIABLES
Directions: Determine the quantities that change (or
the variables) in each of the following situation. Item
number 1 is done as an example.
1. Rosario is making souvenirs for a friend’s wedding.
The number of invited people to attend the wedding
determines the number of souvenirs she must make.
The variables are:
the number of invited people
the number of souvenirs

3. ACTIVITY 1: THE VARIABLES
Directions: Determine the quantities that
change (or the variables) in each of the following
situation. Item number 1 is done as an example.
2. George is selling brownies
online. The more brownies he sells,
the more money he earns. The
variables are:

4. ACTIVITY 1: THE VARIABLES
Directions: Determine the quantities that change (or
the variables) in each of the following situation. Item
number 1 is done as an example.
3. A bakery in Cabadbaran City sells
different types of bread. The more
bread the customers buy, the more
sacks of flour they will use. The
variables are:

5. INDEPENDENT VARIABLE
is a variable that will change by taking
on different values. It changes
independently. In a relation,
independent variable controls the
dependent variable. It is generally
represented by the −variable or
𝑥
what is referred to as the −value.
𝑥

6. DEPENDENT VARIABLE
is a variable that is affected by the
independent variable, and it changes
in response to the independent
variable. In a relation, dependent
variable depends on the independent
variable. It is generally represented by
the −variable or what is referred to
𝑦
as the −value.
𝑦

7. In the scenario, which must
happen first before the other
occurs? Which variable controls
the other, and which variable
depends on the other?

8. DOMAIN OF A FUNCTION
is the set of all acceptable inputs.
Generally, domain is the set of 𝑥
−values or the abscissa of the ordered
pairs of a function.

9. DOMAIN OF A FUNCTION
When represented as ordered pairs is
the set of the first coordinates or it is
the set of all values that can be used
for the independent variable. In the
function y=2/x
The domain is the set of all nonzero
real numbers since 2/x is undefined for
x=0.

10. RANGE OF A FUNCTION
is the set of resulting outputs.
Generally, range is the set of −values
𝑦
or the ordinate of the ordered pairs of
a function.

11. RANGE OF A FUNCTION
Is the set of second coordinates or the
set of all values of the dependent
variables.

12. Defn: A relation is a set of ordered pairs.
     
 
2
,
4
,
2
,
4
,
1
,
1
,
1
,
1
,
0
,
0 


A
 :
A
range
 
4
,
1
,
0
 
2
,
1
,
0
,
1
,
2 

Domain: The x values of the ordered pair.
 :
A
domain
Range: The y values of the ordered pair.
3.5 – Introduction to Functions

13. :
range  
6
,
5
,
4
,
3
 
3
,
2
,
1
,
4

:
domain
x y
1 3
2 5
-4 6
1 4
3 3
x y
4 2
-3 8
6 1
-1 9
5 6
x y
2 3
5 7
3 8
-2 -5
8 7
:
range  
9
,
8
,
6
,
2
,
1
 
6
,
5
,
4
,
1
,
3 

:
domain
:
range  
8
,
7
,
3
,
5

 
8
,
5
,
3
,
2
,
2

:
domain
State the domain and range of each relation.
3.5 – Introduction to Functions

14. Defn: A function is a relation where every x value has one and
only one value of y assigned to it.
x y
1 3
2 5
-4 6
1 4
3 3
x y
4 2
-3 8
6 1
-1 9
5 6
x y
2 3
5 7
3 8
-2 -5
8 7
function not a function function
State whether or not the following relations could be a
function or not.
3.5 – Introduction to Functions

15. Functions and Equations.
3
2 
 x
y
x y
0 -3
5 7
-2 -7
4 5
3 3
x y
2 4
-2 4
-4 16
3 9
-3 9
x y
1 1
1 -1
4 2
4 -2
0 0
2
x
y  2
y
x 
function function not a function
State whether or not the following equations are functions or
not.
3.5 – Introduction to Functions

16. Vertical Line Test
Graphs can be used to determine if a relation is a
function.
If a vertical line can be drawn so that it intersects a
graph of an equation more than once, then the equation
is not a function.
3.5 – Introduction to Functions

17. x
y
The Vertical Line Test
3
2 
 x
y
x y
0 -3
5 7
-2 -7
4 5
3 3
function
3.5 – Introduction to Functions

18. x
y
2
x
y 
x y
2 4
-2 4
-4 16
3 9
-3 9
The Vertical Line Test
function
3.5 – Introduction to Functions

19. x
y
2
y
x 
x y
1 1
1 -1
4 2
4 -2
0 0
The Vertical Line Test
not a function
3.5 – Introduction to Functions

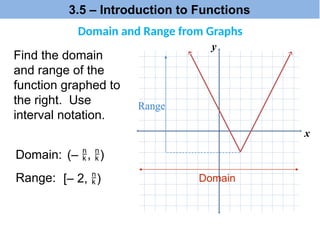
20. Find the domain and
range of the function
graphed to the right.
Use interval
notation.
x
y
Domain:
Domain
Range:
Range
[–3, 4]
[–4, 2]
Domain and Range from Graphs
3.5 – Introduction to Functions

21. Find the domain
and range of the
function graphed to
the right. Use
interval notation.
x
y
Domain:
Domain
Range:
Range
(– , )
[– 2, )
Domain and Range from Graphs
3.5 – Introduction to Functions

22. Function Notation
  1
3 
 x
x
f
  1
3 
 x
x
y
   
x
f
x
y
y 

Shorthand for stating that an equation is a function.
1
3 
 x
y
Defines the independent variable (usually x) and the
dependent variable (usually y).
3.6 – Function Notation

23.   5
2 
 x
x
f
Function notation also defines the value of x that is to be use
to calculate the corresponding value of y.
    5
3
2
3 

f
  1
3 
f
 
1
,
3
f(x) = 4x – 1
find f(2).
f(2) = 4(2) – 1
f(2) = 8 – 1
f(2) = 7
(2, 7)
g(x) = x2
– 2x
find g(–3).
g(–3) = (-3)2
– 2(-3)
g(–3) = 9 + 6
g(–3) = 15
(–3, 15)
find f(3).
3.6 – Function Notation

24. Given the graph of
the following function,
find each function
value by inspecting
the graph.
f(5) = 7
x
y
f(x)
f(4) = 3
f(5) = 1
f(6) = 6
●
●
●
●
3.6 – Function Notation

25. 3.6 – Function Notation