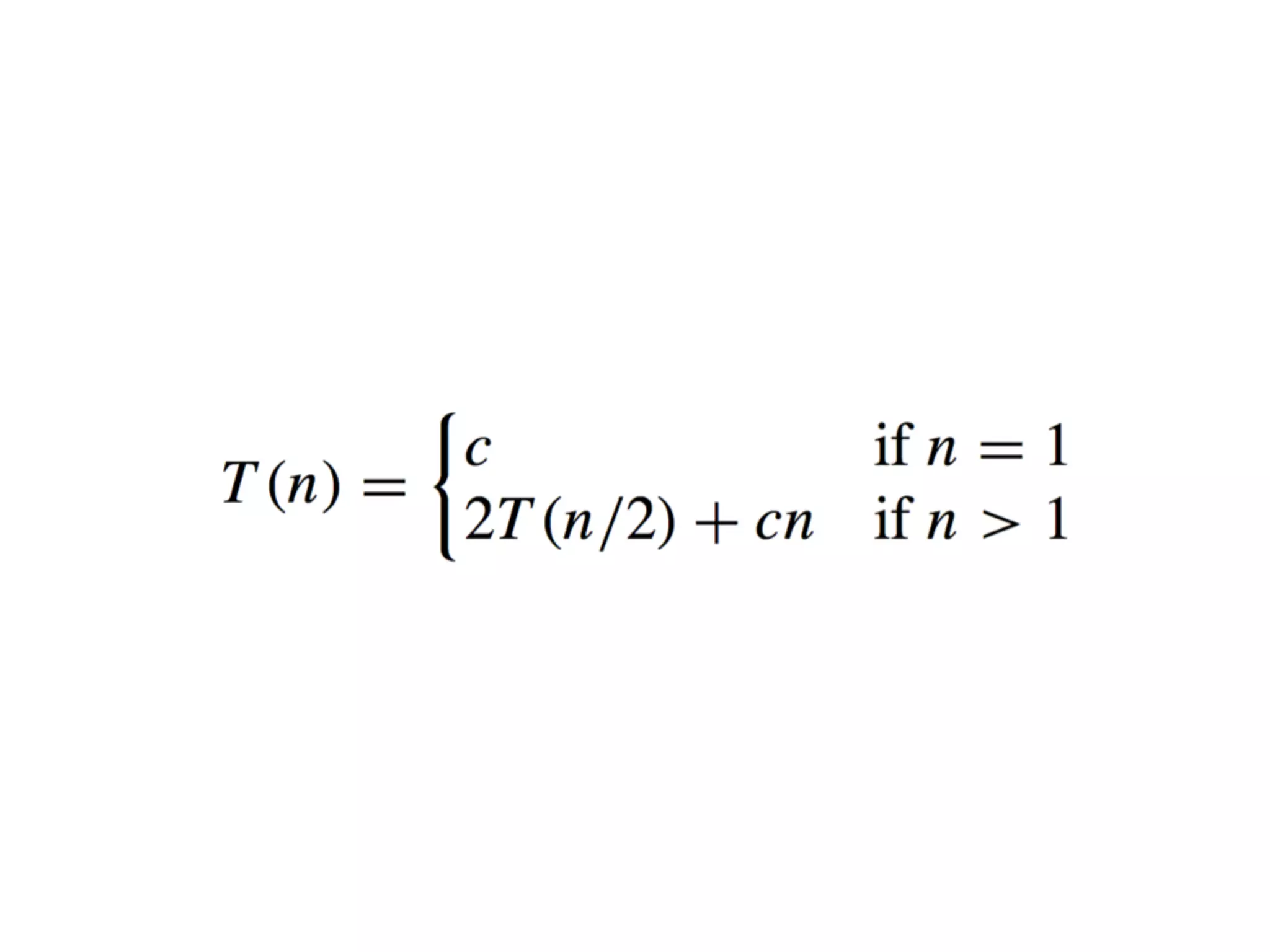The document discusses the CS 321 Algorithm Analysis and Design course. It covers announcements about homework, grading, and clarifications. Algorithm analysis is introduced, covering running time and correctness. Insertion sort is presented, including a loop invariant and examples. Best-case, average-case, and worst-case running times are defined. Asymptotics and big O notation are introduced. Merge sort is mentioned along with induction.




![Announcements
The first homework will be online this Wednesday
with a deadline of next Wednesday.
Please take the informal survey on the website,
or send me an email with the subject [CS321].
Will deal with clarifications on Friday.](https://image.slidesharecdn.com/0204jansortingcontd-160212160458/75/02-04-Jan-Sorting-Continued-5-2048.jpg)






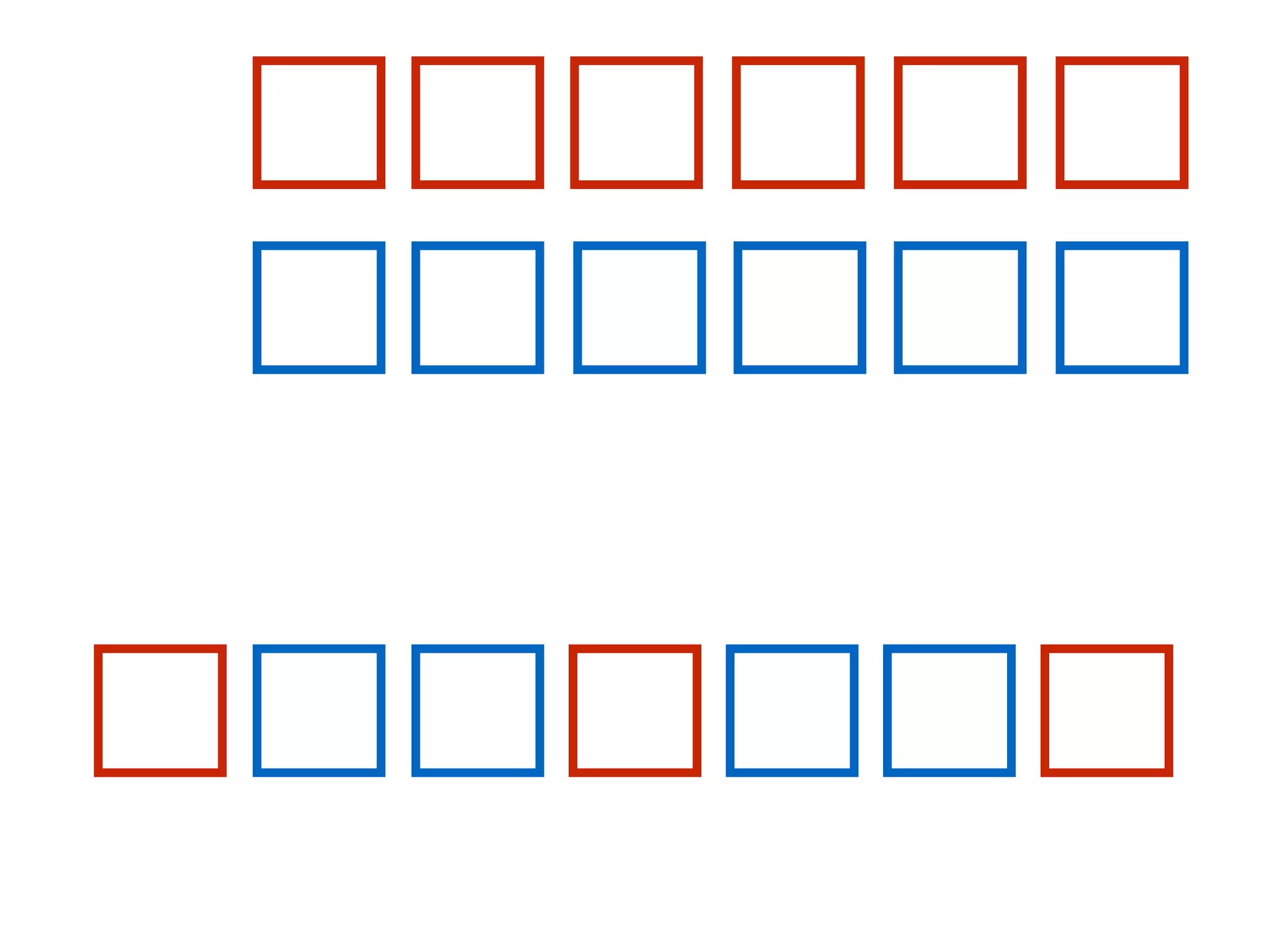
![At the start of each iteration of the for loop of lines 1–8,
the subarray A[1 . . j − 1] consists of the elements
originally in A[1 . . j − 1] but in sorted order.](https://image.slidesharecdn.com/0204jansortingcontd-160212160458/75/02-04-Jan-Sorting-Continued-12-2048.jpg)




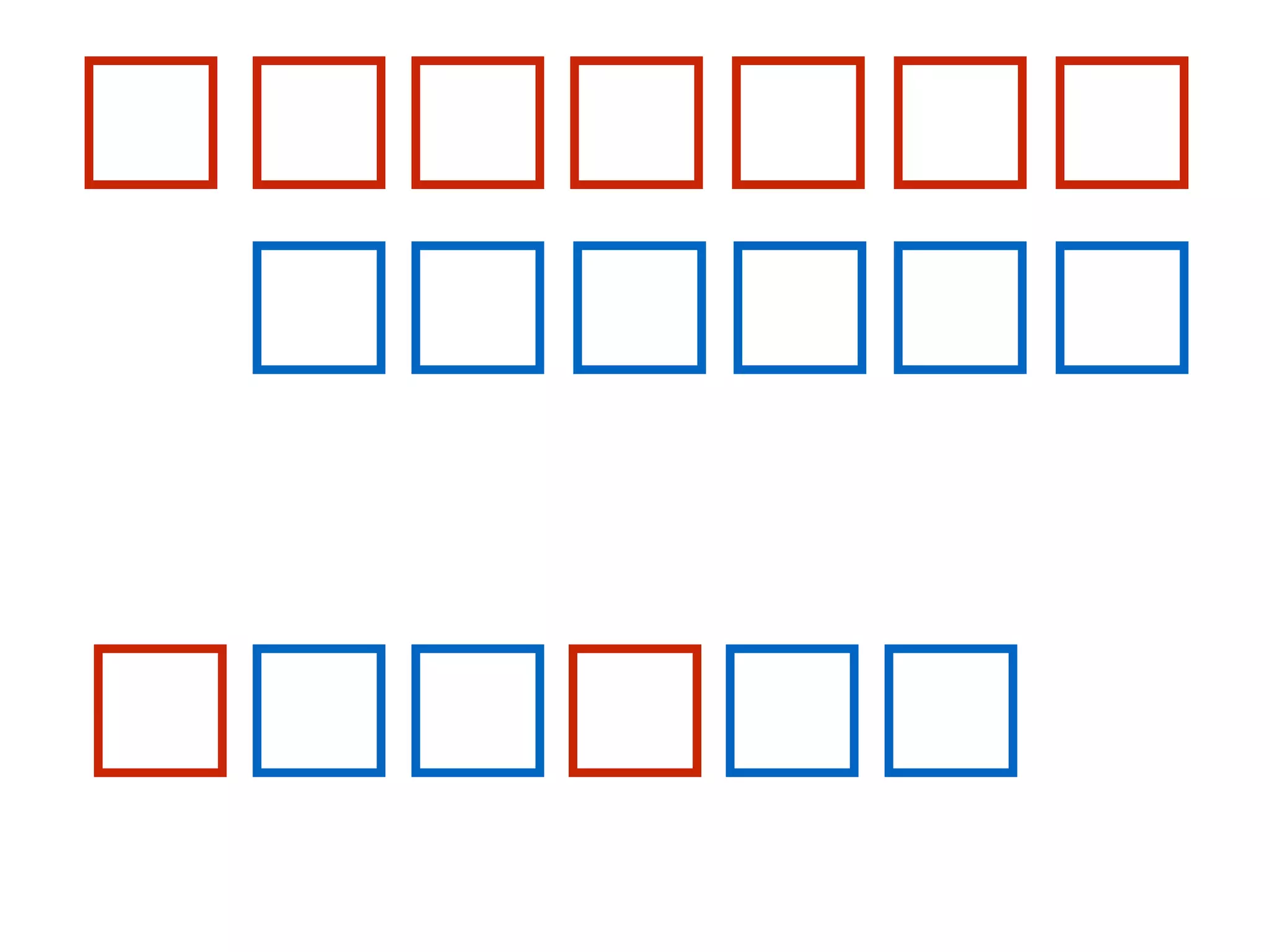
![At the start of each iteration of the for loop of lines 1–8,
the subarray A[1 . . j − 1] consists of the elements
originally in A[1 . . j − 1] but in sorted order.](https://image.slidesharecdn.com/0204jansortingcontd-160212160458/75/02-04-Jan-Sorting-Continued-17-2048.jpg)
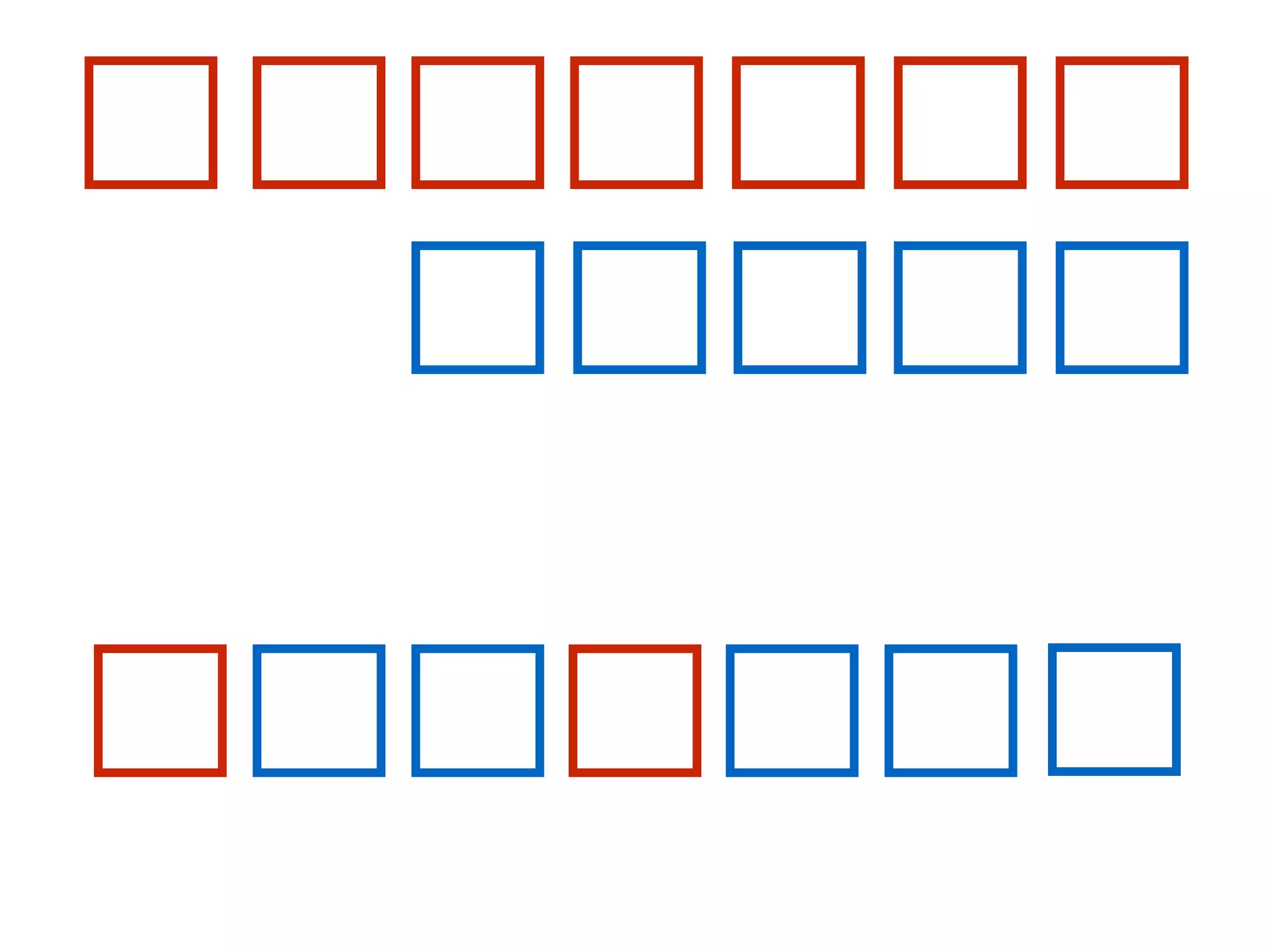
![At the start of each iteration of the for loop of lines 1–8,
the subarray A[1 . . j − 1] consists of the elements
originally in A[1 . . j − 1] but in sorted order.](https://image.slidesharecdn.com/0204jansortingcontd-160212160458/75/02-04-Jan-Sorting-Continued-18-2048.jpg)
![At the start of each iteration of the for loop of lines 1–8,
the subarray A[1 . . j − 1] consists of the elements
originally in A[1 . . j − 1] but in sorted order.](https://image.slidesharecdn.com/0204jansortingcontd-160212160458/75/02-04-Jan-Sorting-Continued-19-2048.jpg)





![[1,2,3]
[1,3,2]
[3,1,2]
[2,1,3]
[2,3,1]
[3,2,1]](https://image.slidesharecdn.com/0204jansortingcontd-160212160458/75/02-04-Jan-Sorting-Continued-25-2048.jpg)









![[Chapter 2, KT]
Running times on processors performing a
million high-level operations per second.](https://image.slidesharecdn.com/0204jansortingcontd-160212160458/75/02-04-Jan-Sorting-Continued-35-2048.jpg)
![[Chapter 2, KT]
Running times on processors performing a
million high-level operations per second.](https://image.slidesharecdn.com/0204jansortingcontd-160212160458/75/02-04-Jan-Sorting-Continued-36-2048.jpg)