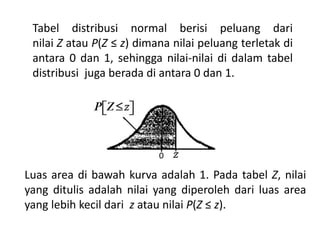
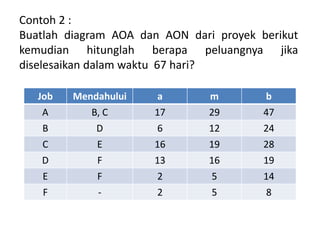
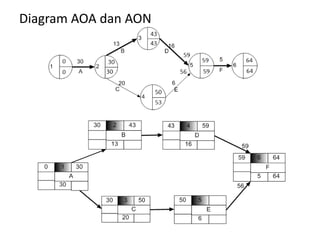
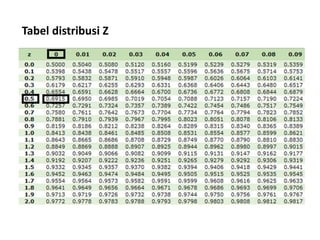
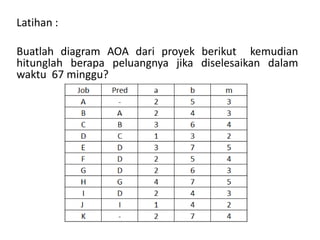
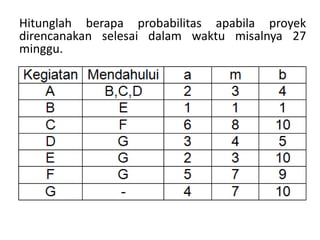
Dokumen tersebut menjelaskan tentang analisis waktu proyek menggunakan metode PERT (Project Evaluation and Review Technique). Metode PERT menggunakan tiga estimasi waktu pelaksanaan kegiatan (optimis, mungkin, pesimis) untuk menghitung rata-rata dan variansi waktu proyek secara statistik. Dokumen tersebut memberikan contoh perhitungan metode PERT dan menggunakan tabel distribusi normal untuk memperkirakan peluang penyelesaian

1. Analisa Waktu Proyek Dengan
Metode PERT
Simon Patabang, ST., MT.
Universitas Atma Jaya Makassar

2. Pendahuluan
Durasi kegiatan dalam proyek dapat ditentukan dengan
2 metode yaitu :
1. CPM (Critical Path Method)
2. PERT (Project Evaluation and Review Technique)
Dengan CPM, durasi kegiatan merupakan variabel
tetap. Misalnya pada contoh yang telah dibahas
sebelumnya. Sedangkan dengan metode PERT, durasi
kegiatan merupakan variabel tidak tetap atau
berdasarkan taksiran.

3. Definisi
• PERT adalah suatu metode analisis yang
dirancang untuk membantu dalam
penjadwalan dan pengendalian proyek-proyek
yang kompleks. (T. Hari Handoko, 1993)
• PERT adalah suatu metode analisis jaringan
yang digunakan untuk memperkirakan durasi
kegiatan proyek yang sangat tidak pasti.

4. Metodologi PERT
• Metodologi PERT menggunakan diagram
jaringan yang menggambarkan kegiatan dari
sebuah proyek.
• Diagram kegiatan dapat dibuat dengan
menggunakan diagram AOA atau AON

5. Berdasarkan metode PERT, ada 3 macam taksiran waktu
pelaksanaan suatu kegiatan yaitu :
1. Waktu paling optimis adalah taksiran waktu paling
cepat untuk menyelesaikan suatu kegiatan,
dinyatakan dengan simbol a.
2. Waktu paling mungkin adalah taksiran waktu
normal untuk menyelesaikan suatu kegiatan,
dinyatakan dengan simbol m.
3. Waktu paling pesimis adalah taksiran waktu yang
paling lama untuk menyelesaikan suatu kegiatan,
dinyatakan dengan simbol b.
Waktu Kegiatan

6. Taksiran Waktu Kegiatan
• Waktu kegiatan yang diharapkan (expected time)
dinyatakan dengan rumus:
4
6
a m b

 

• Hubungan antara nilai a, b, dan m dinyatakan dalam
distribusi Z sebagai berikut :

7. dan deviasi standar kegiatan (σk) dinyatakan dengan
persamaan :
dan deviasi standar proyek (σP) dinyatakan dengan
persamaan :
2
P k  
6
k
b a




8. Waktu penyelesaian proyek ditentukan dengan
distribusi normal Z yang dinyatakan dengan
persamaan :
X adalah waktu penyelesaian proyek yang mungkin
dilakukan.
μ adalah durasi rata-rata dari kegiatan atau waktu yang
diharapkan
Z adalah peluang penyelesaian proyek (lihat Tabel
distibusi Z)
P
X
Z





9. Luas area di bawah kurva adalah 1. Pada tabel Z, nilai
yang ditulis adalah nilai yang diperoleh dari luas area
yang lebih kecil dari z atau nilai P(Z ≤ z).
Tabel distribusi normal berisi peluang dari
nilai Z atau P(Z ≤ z) dimana nilai peluang terletak di
antara 0 dan 1, sehingga nilai-nilai di dalam tabel
distribusi juga berada di antara 0 dan 1.

10. Contoh:
Kegiatan Mendahului
Deviasi
Standar (σ)
Waktu rata-rata
–Hari (μ)
A D, C 4 12
B E 12 30
C E 7 20
D Tidak Ada 10 25
E Tidak Ada 4 10
Diagram AOA :

11. Jalur kritis ditentukan oleh durasi rata2 kegiatan:
AD = 12 + 25 = 37
BE = 30 + 10 = 40
ACE = 12 + 20 + 10 = 42  ACE adalah Jalur Kritis
Maka waktu rata-rata penyelesaian proyek yang
diharapkan adalah :
σk = μA + μC + μE = 42 hari
Deviasi standar proyek σp adalah:
σp = √(σ²A + σ²C + σ²E) = √(4² + 7² + 4²)
σp = √ (81) = 9 hari.

12. • Dengan hasil perhitungan durasi rata-rata dan
deviasi standart proyek, maka kita dapat menghitung
berapa persen kemungkinan proyek dapat
diselesaikan untuk x hari.
• Misalnya, berapa persen peluang proyek dapat
selesai dalam waktu 60 hari?
X = 60 hari, σp = 9 hari, μ = 42 hari maka Z adalah :
P
X
Z





13. • Dalam daftar Tabel distribusi normal, diperoleh
untuk Z = 2 terdapat luas di bawah kurva. Untuk x ≤
60 adalah 0,9772.
• Artinya bahwa peluang proyek dapat diselesaikan
dalam waktu 60 hari adalah 97,72 %.

14. Job Mendahului a m b
A B, C 17 29 47
B D 6 12 24
C E 16 19 28
D F 13 16 19
E F 2 5 14
F - 2 5 8
Contoh 2 :
Buatlah diagram AOA dan AON dari proyek berikut
kemudian hitunglah berapa peluangnya jika
diselesaikan dalam waktu 67 hari?

15. • Hitung µ dan σk. Hasilnya seperti pada tabel.
Job Mend a m b μ σk
A B, C 17 29 47 30 5
B D 6 12 24 13 3
C E 16 19 28 20 2
D F 13 16 19 16 1
E F 2 5 14 6 2
F - 2 5 8 5 1
• Gambar diagram AOA dan AON dengan durasi kegiatan
adalah µ.

16. Diagram AOA dan AON

17. Jalur kritis : ABDF = 64 hari ( µ = waktu yang diharapkan).
Secara statistik, probabilitas selesainya proyek sebelum
waktu yang dijadwalkan dapat dihitung dengan distribusi
normal Z.
Hitung varian proyek σp :
2 2 2 2
(5 3 1 1 )P    
6P 
dimana :
P
X
Z



 2
P k  

18. • Dari soal diketahui x = 67 maka :
Z = (67 - 64) / 6
Z = 3/6 = 0,5  dari tabel z diperoleh P =
0,6915
Peluang 69,15% untuk menyelesaikan proyek
dalam waktu 67 hari
P
X
Z





19. Kurva Distribusi normal Z

20. Tabel distribusi Z

21. Latihan :
Buatlah diagram AOA dari proyek berikut kemudian
hitunglah berapa peluangnya jika diselesaikan dalam
waktu 67 minggu?

22. Hitunglah berapa probabilitas apabila proyek
direncanakan selesai dalam waktu misalnya 27
minggu.

23. Sekian