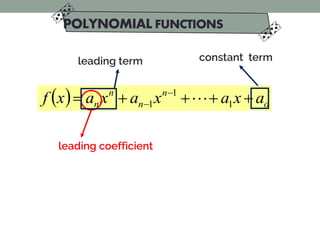
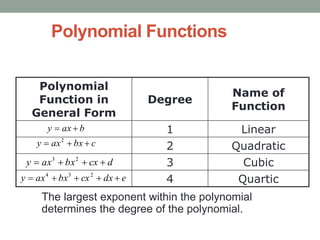
This document discusses polynomial functions. It defines polynomial expressions and equations. The objectives are to recall concepts of polynomial expressions, illustrate polynomial functions, and find the degree and leading term. It provides examples of determining if something is a polynomial expression and examples of writing polynomial functions in standard form. It also defines the degree, leading coefficient, and constant term of a polynomial function.

1. POLYNOMIALS

2. POLYNOMIAL
FUNCTIONS
MODULE 3

3. OBJECTIVES
At the end of the lesson, the students
should be able to:
1. Recall the concepts of polynomial
expression.
2. Illustrate a polynomial function.
3. Find the degree and the leading term of a
polynomial function.

4. Review: Polynomials
Polynomial Expression
anXn +an-1Xn-1+ an-2Xn-2 + …+ a1X + a0
Polynomial Equation
anXn +an-1Xn-1+ an-2Xn-2 + …+ a1X + a0 = 0
Polynomial expression
Polynomial equation

5. ACTIVITY 1 – Which is which?
Determine whether each of the following is a polynomial expression
or not. On your miniboards write Y is the expression is polynomial; x
if it is not a polynomial. Give reasons.

6. ACTIVITY 1 – Which is which?

7. POLYNOMIAL FUNCTIONS
CONDITIONS:
1. Each exponent is a whole number.
2. Denominators contain no variable in x.
3. No variable is under the radical sign.

8. A polynomial function is a function of the form:
( ) o
n
n
n
n a
x
a
x
a
x
a
x
f +
+
+
+
= −
− 1
1
1 
All of these coefficients are real numbers
n must be a positive integer
The degree of one variable polynomial is the
largest power on any x term in the polynomial.
an ≠ 0

9. POLYNOMIAL FUNCTIONS
( ) o
n
n
n
n a
x
a
x
a
x
a
x
f +
+
+
+
= −
− 1
1
1 
leading term
leading coefficient
constant term

10. 1. f(x) = anXn an-1Xn-1+ an-2Xn-2 + …+ a1X + a0
POLYNOMIAL FUNCTION
• an is called the leading coefficient
• n is the degree of the polynomial
• a0 is called the constant term
*Standard Form – polynomials are written in
descending powers of x.
Polynomial function can be written in
different ways:
2. y = anXn an-1Xn-1+ an-2Xn-2 + …+ a1X + a0
y = x4 + 2x3 –x2 +14x – 56 in factored form is
y = (x2 + 7)(x -2 )(x + 4)

11. Examples:
1.) f(x) = 2x3 – 10x + x4 – 13x2
Standard form:
Degree:
Leading Coefficient:
Constant Term:
2.) y = -45 + 45x2 + 66x + 6x3
Standard form:
Degree:
Leading Coefficient:
Constant Term:
POLYNOMIAL FUNCTION
f(x) = x4 + 2x3 – 13x2 –
10x
4
1
0
f(x)=6x3 + 45x2 + 66x - 45
3
6
-45

12. Polynomial Functions
Polynomial
Function in
General Form
Degree
Name of
Function
1 Linear
2 Quadratic
3 Cubic
4 Quartic
The largest exponent within the polynomial
determines the degree of the polynomial.
e
dx
cx
bx
ax
y +
+
+
+
= 2
3
4
d
cx
bx
ax
y +
+
+
= 2
3
c
bx
ax
y +
+
= 2
b
ax
y +
=

13. ACTIVITY 2 – Fix and Move Them, then Fill
Me Up